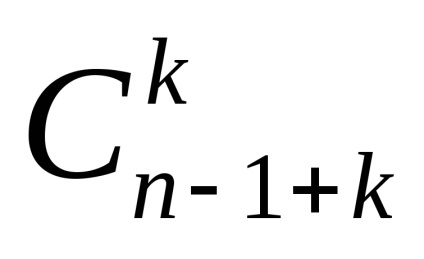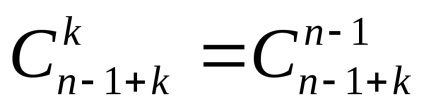Teorema 2. Numărul total al eșantioanelor din schema de selecție k a elementelor de la n fără returnare și ținând cont de ordine este dat de formula
și se numește numărul de alocări de la elemente la celule.
Dovada. Prima minge poate fi aleasă în moduri. Cu fiecare dintre aceste metode, a doua minge poate fi selectată în mod n-1, etc. Ultima minge k poate fi aleasă (n-k + 1). Prin teorema 1. numărul total de opțiuni este
care urma să fie dovedită.
Corolar 1. Numărul de permutări posibile ale unui set de elemente n este n!
D
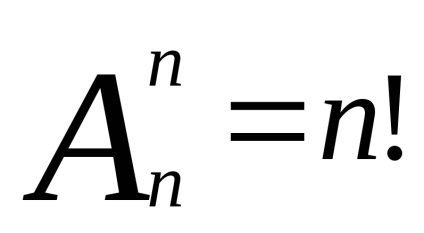
Schema urn: alegere fără întoarcere și fără a lua în considerare ordinea
Teorema 3. Numărul total al eșantioanelor din schema de selecție pentru elementele k de la fără a se întoarce și fără a lua în considerare ordinea este dat de
și
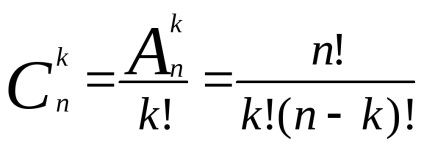
Dovada. Menționăm că, conform Corolarului 1. Din fiecare probă dintr-o compoziție dată (constând din elemente k), se poate forma k! selecții, care se deosebesc una de alta numai în ordinea elementelor.
Asta este numărul de probe care diferă în ordine și în k! ori mai mult decât numărul de eșantioane care diferă doar prin compoziție. despărțitor
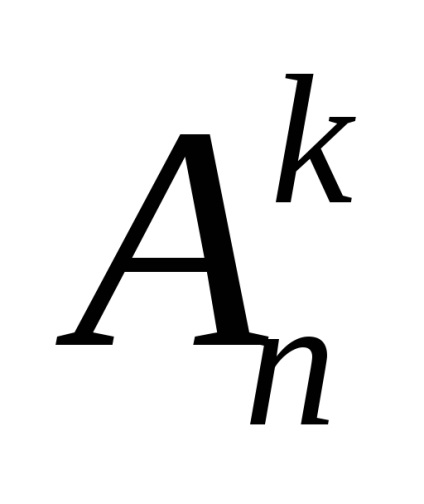
Schema urn: o alegere cu revenire și luând în considerare ordinea
T
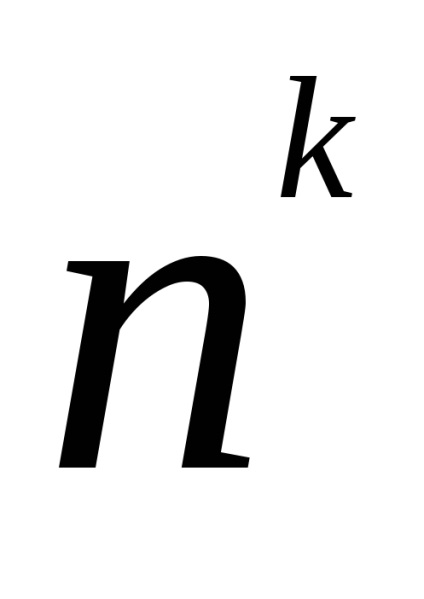
Dovada. Prima minge poate fi aleasă în moduri. Cu fiecare dintre aceste metode, cea de-a doua minge poate fi de asemenea selectată în moduri innoptare, și sok ori.
Schema Urn: alegere cu întoarcere și fără comandă
Luați în considerare o urnă cu două bile și listați rezultatele selectării a două bile de la această urnă atunci când alegeți cu un randament:
Luând în considerare ordinea
Observăm că în schemă "fără a ține cont de ordin", s-au obținut 3 rezultate diferite, spre deosebire de cele patru din schema de "luare în considerare a ordinului". (numărul 4 apare și conform teoremei 4); și că nici o împărțire în "numărul oricărei permutări" va duce la obținerea numărului 3 din 4.
T
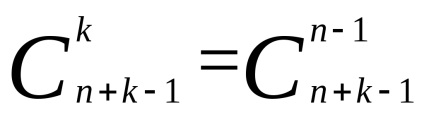
Dovada. Să analizăm în detaliu modul în care cele două rezultate diferite ale unei astfel de scheme de selecție diferă una de cealaltă. Nu ne pasă de ordinea numerelor, adică luăm în considerare numai de câte ori în colecția noastră de numere de minge a apărut numărul 1 al mingii, numărul 2, .... număr de mărgele. Asta este rezultatul alegerii poate fi reprezentat de un set de numere k1, k2, ... kn. în care k este numărul de apariții ale numărului de minge i din proba și k1 + k2 + ... + kn = k. În acest caz, cele două rezultate ale experimentului sunt diferite dacă seturile corespunzătoare k1, k2, ..., kn nu coincid.
Imaginați-vă un alt experiment care are exact aceleași rezultate (și, prin urmare, există cât mai multe dintre acestea). Sunt n cutii în care sunt plasate bilele. Suntem interesați doar de numărul de bile din fiecare cutie. Asta este rezultatul experimentului este din nou setul de numere k1, k2, ... kn. în care ki este numărul de bile în cutia cu numărul i. și k1 + k2 + ... + kn = k. Numerele încă iau valori naturale sau egale cu 0.
Acum, să descriem rezultatul unei astfel de plasări sub forma unei scheme în care liniile verticale denotă partiții între cutii, iar cercurile sunt bile în cutii:
Vedem rezultatul plasării a 9 bile în 7 cutii. Există prima casetă 3 cuprinde o minge, pe cutii a 2 si 6 sunt goale, 3 caseta 1 cuprinde o minge și în casetele 4 și 5 2 au mingea. O minge pentru a trece de la prima casetă în al doilea și, în același mod descrie un alt rezultat al adăugării:
Vedem că toate de cazare pot fi obținute prin schimbarea reciproc bile și pereți, sau bile rasstavlyayak nan-1 + K loc. Chislon-1 + k se obține după cum urmează: sertare au rovnon + □ DN 1 partiție, considerând extremă, sau n-1 partiție, cu excepția extremă, care nu poate fi mutat. Și există și bile. După ce a trecut prin toate căile posibile de rasstavitk bile pe etihn-1 + k locații (și punerea în spațiul despărțitor rămas), itera prin toate încăperile de locuit necesare.
Dar modalitățile de a organiza k balls pe n-1 + k locuri exact