Deterministică mașină Turing
Turing Machine (MT) - executor abstract (computer abstract). A fost propusă de Alan Turing în 1936 pentru a formaliza conceptul de algoritm.
Mașina Turing este o extensie a automatului finit și, conform tezei Bisericii-Turing. poate imita toți ceilalți artiști (prin specificarea regulilor de tranziție) care implementează cumva procesul de calcul pas cu pas, în care fiecare etapă a calculului este destul de elementară.
Construcția unei mașini Turing
Mașina Turing constă dintr-o centură fără sfârșit în ambele direcții (mașinile Turing sunt posibile care au mai multe benzi infinite), împărțite în celule și un dispozitiv de comandă. capabile să se afle într-una din numeroasele state. Numărul de stări posibile ale dispozitivului de comandă este definit fin și precis.
Unitatea de control funcționează în conformitate cu regulile de tranziție. care reprezintă algoritmul implementat de această mașină Turing. Fiecare regulă de tranziție necesită aparatul, în funcție de starea actuală și observată în celula actuală de caractere, pentru a scrie în celulă un nou simbol, trece la o nouă stare și pentru a muta o celulă la stânga sau la dreapta. Unele stări ale mașinii Turing pot fi etichetate ca terminale. iar trecerea la oricare dintre ele inseamna sfarsitul muncii, oprirea algoritmului.
O mașină Turing se numește deterministă. dacă fiecare combinație de simbol de stare și bandă din tabel corespunde nu mai mult de o regulă. Dacă există o pereche (simbol bandă - stare) pentru care există 2 sau mai multe instrucțiuni, o astfel de mașină Turing este numită nondeterministică.
Descrierea mașinii Turing
Mașină specifică Turing este setat listarea alfabetul elemente ale multimii A, mulțimea Q de state și un set de reguli prin care operează aparatul. Ei au forma :. Qi aj → qi1 AJ1 dk (în cazul în care capul este în qi de stat si a observat celule scrisoare scrisă aj cap se mută în statul qi1 celula în loc să aj înregistrat capul AJ1 face dk mișcare, care are trei opțiuni ....: la celula din stânga (L), la celula din dreapta (R), pentru a rămâne în poziție (H)). Pentru fiecare configurație posibilă
Exemplu de mașină Turing
Iată un exemplu de MT pentru înmulțirea numerelor într-un sistem de numere unare. Mașina funcționează în conformitate cu următorul set de reguli:
Protocolul specifică starea inițială și cea finală a MT, configurația inițială pe bandă și locația capului mașinii (simbolul subliniat).
Completitudinea lui Turing
Putem spune că mașina Turing este un calculator simplu cu memorie liniară, care, conform regulilor formale, convertește datele de intrare printr-o secvență de acțiuni elementare. Acțiunea elementară este că acțiunea schimbă doar o mică parte a datelor în memorie (în cazul mașinii Turing - numai o singură celulă), iar numărul de acțiuni posibile este finit. În ciuda simplității mașinii Turing, este posibil să se calculeze tot ce poate fi calculat pe orice altă mașină care efectuează calcule folosind o secvență de operații elementare. Această proprietate se numește exhaustivitate.
Una dintre modalitățile naturale de a demonstra că algoritmii de calcul care pot fi implementați pe o singură mașină pot fi implementați pe de altă parte, este simularea primei mașini pe cea de-a doua.
Așa cum sa spus, pe Mașina Turing este posibil să se simuleze (prin stabilirea regulilor de tranziție) toți ceilalți artiști care realizează cumva procesul de calcul pas cu pas, în care fiecare etapă a calculului este destul de elementară.
Pe mașina Turing, puteți simula mașina Postului. algoritmi normali Markov și orice program pentru computerele obișnuite care convertesc datele de intrare în ieșire printr-un algoritm. La rândul său, pe diferiți artiști abstracți, este posibil să imităm mașina Turing. Interpreții, pentru care acest lucru este posibil, se numesc Turing complet (Turing complete).
Există programe pentru computerele obișnuite care imită lucrarea mașinii Turing. Dar trebuie remarcat faptul că această imitație este incompletă, deoarece există o bandă abstractă infinită în Mașina Turing. O bandă fără sfârșit cu datele imposibil de a simula pe deplin pe un calculator cu o memorie finită (memoria totală de calculator - RAM, hard disk-uri, diverse externe medii de stocare, registre, și memoria cache CPU, etc -. Fii foarte mare, dar, cu toate acestea, întotdeauna este finit).
Variante ale mașinii Turing
Modelul mașinii Turing permite extensii. Puteți lua în considerare mașinile Turing cu un număr arbitrar de benzi și benzi multidimensionale cu constrângeri diferite. Cu toate acestea, toate aceste mașini sunt complete în Turing și modelate de o mașină convențională Turing
Mașină Turing care lucrează pe o bandă semi-infinită
Ca exemplu de astfel de informații, luați în considerare următoarea teoremă: Pentru orice mașină Turing, există o mașină Turing echivalentă care funcționează pe o bandă semi-infinită.
Luați în considerare dovada dată de Yu.G. Karpov în cartea sa Theory of Automata. Dovada acestei teoreme este constructivă, adică vom da un algoritm prin care o mașină Turing echivalentă cu proprietatea declarată poate fi construită pentru orice mașină Turing. În primul rând, numărăm aleatoriu celulele benzii de lucru MT, adică definiți noua locație a informațiilor de pe bandă:
Apoi renumerotăm celulele și vom presupune că simbolul "*" nu este conținut în dicționarul MT:
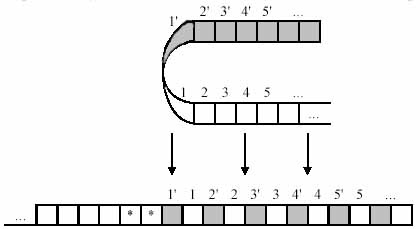
În cele din urmă, schimbați aparatul Turing, dublarea numărului statelor sale, și de a schimba trecerea de cap de citire-scriere, astfel încât un grup de statut mașină ar fi echivalentă cu activitatea sa în zona umbrită, în timp ce celălalt grup a mașinii de stat ar lucra ca lucrările de mașini originale într-o zonă neimpozată. Dacă simbolul "*" apare în operația MT, atunci capul de citire și scriere a atins limita zonei:
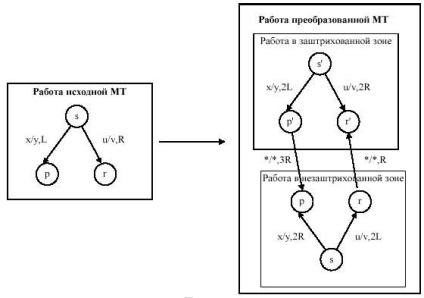
Starea inițială a noii mașini Turing este setată în una sau în cealaltă zonă, în funcție de ce parte a benzii sursă capul de citire și scriere este în configurația inițială. Evident, banda în mașina echivalentă Turing nu este folosită la stânga marcatorilor de marcare "*".