Fig. 1 3. Prin un anumit punct, trageți o linie de poziție generală sau particulară.
În Fig. 1, q dă condiția inițială a problemei - punctul A. Fig. 1, e, x și, respectiv, prin punctul A, linia dreaptă l A în poziția generală, linia frontală i A, linia dreaptă a profilului p A.
4. Construiți o linie care aparține suprafeței date (figurile 2, 3): 1) Plot.
În Fig. 2, iar condiția inițială a problemei este dată, planul T (ABC) al poziției generale. În Fig. 2b, liniile l și m ale poziției generale aparținând lui sunt construite, fiecare fiind definită de două puncte - l (1 - 2) T, m (3 - C) T. Fig. 2, am construit planul orizontal h (1 - C) Γ aparținând planului Γ (ABC), frontul f (2 - C) Γ, linia profilului p (3 - 4) Γ. Fig. 2, d, q, c sunt construite linii drepte de poziție generală ce aparțin, respectiv, planurilor frontale, orizontale și ale profilului - lm n.
2) Mnogogranicheskoy poverezhnosty.
În Fig. 3 și sunt construite segmente drepte [1 - 2] și [5 - 3], aparținând suprafeței piramidei, în fig. 3, 6 - [1 - 2], care aparține suprafeței prismei.
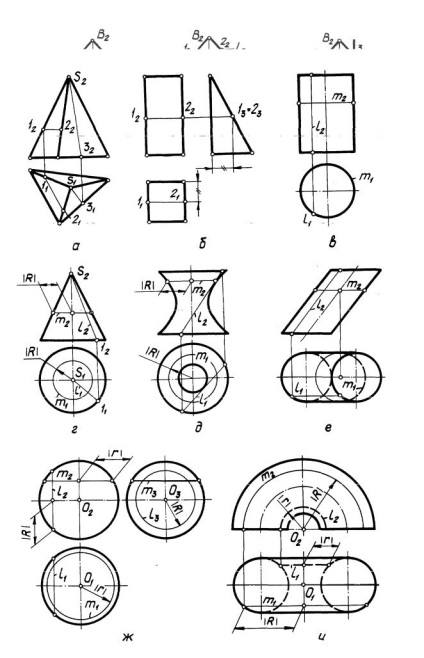
3) C u a n io n u p u r a n e r.
În Fig. 3, c, d, d, generatoarele rectiliniare l (l 1 l 2) și paralelele m (m 1 m 2) aparținând suprafețelor de rotație conduse sunt construite în Fig. 3, e este generatorul rectiliniu l (l 1 l 2) și cercul m (m 1 m 2)
a unui cilindru eliptic cu o bază circulară, în fig. 3, x, iar paralelele m și l sunt construite. aparținând suprafețelor neliniare de revoluție.
5. Construiți o a doua proiecție a liniei aparținând suprafeței date, dacă se dă o proiecție a liniei (Figura 2, 4):
1) Parcele.
În Fig. 2, x este dată condiția inițială a problemei - planul T (a // b) și proiecția orizontală [A 1 B 1] a segmentului [AB] care îi aparține. În Fig. 2, m își prezintă soluția. În Fig. 2, k este dată condiția inițială - planul orizontal de proeminență și proiecția frontală l 2 a liniei l care îi aparține. În Fig. 2, problema este rezolvată.
2) Mnogogranicheskoy poverkhnosty.
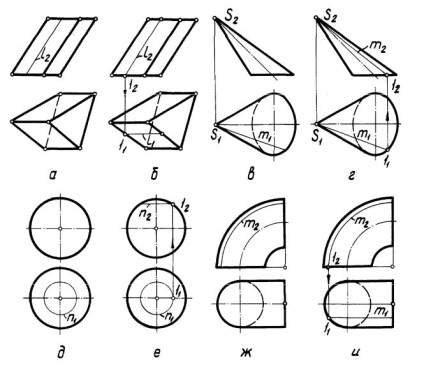
În Fig. 4, iar condiția inițială a problemei este dată - proiecția frontală l 2 a liniei l. deținute. suprafața prismei. În Fig. 4b, problema este rezolvată.
3) C u a n io n u p u r a n e r.
În Fig. 48, c, d, g, este dată una dintre proeminențele liniei aparținând respectiv suprafețelor conului, sferei, torusului. În Fig. 4, r, e, iar soluția problemei este arătată.
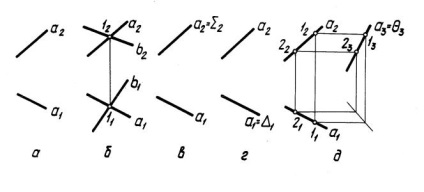
6. Prin această linie dreaptă, trageți un plan de poziție generală sau particulară (Figura 5).
În Fig. 5, iar condiția inițială a problemei este dată de linia a. În Fig. 5 a, b, c, d, q, este desenat un plan de poziție generală F (ab) a, care proiectează planul o proeminență orizontală și care proiectează planul a orizontal.
7. Construiți un punct care aparține suprafeței (Figura 6): 1) Plot.
În Fig. 6, a, b sunt construite punctele ce aparțin planului poziției generale și planului de proiectare frontală.
2) Mnogogranicheskoy poverezhnosty.
În Fig. 6, construim un punct M aparținând suprafeței piramidei SABC.
3) C u a n io n u p u r a n e r.
Punctele aparținând suprafețelor unui con, unui helicoid direct, unui helicoid oblic, unui paraboloid hiperbolic sunt construite în Fig. 6, d, d, e, g.
Notă: Orice linie reprezintă un set de puncte, deci construcția este arbitrară. line, aparținând suprafeței, se bazează pe o soluție multiplă a problemei elementare considerate nr. 7. Pentru un exemplu din Fig. 6, și, k arată construcția liniilor arbitrare care aparțin, respectiv, suprafețelor sferei și a conului.
8. Construiți o a doua proiecție a unui punct care aparține unei suprafețe date dacă este dată una dintre proiecțiile sale (Figura 7):
1) Parcele.
În Fig. 7, a, b sunt date condiția inițială și construcția unui punct A aparținând planului T (lm) în poziție generală.