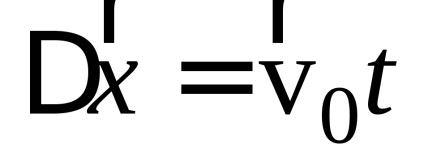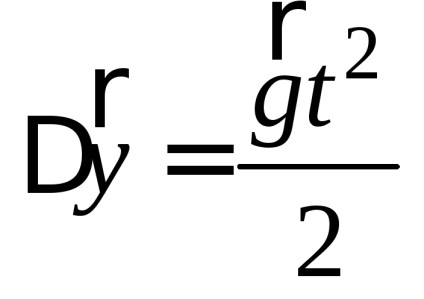1. Corpul a fost aruncat de pe suprafața Pământului la un unghi = 60 la orizont cu o viteză inițială v0 = 20 m / s. Dacă nu țineți cont de rezistența aerului, găsiți:
a) viteza corpului după t = 2 s după începerea mișcării;
b) timpul t1. prin care viteza va fi cu unghiul orizontal β = 30;
c) timpul de zbor al corpului T înainte de a cădea pe Pământ;
d) înălțimea maximă de ridicare H și intervalul de zbor L;
e) ecuația traiectoriei y (x), unde x și y sunt coordonatele corpului.
și
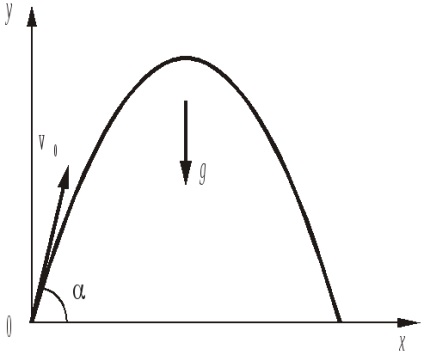
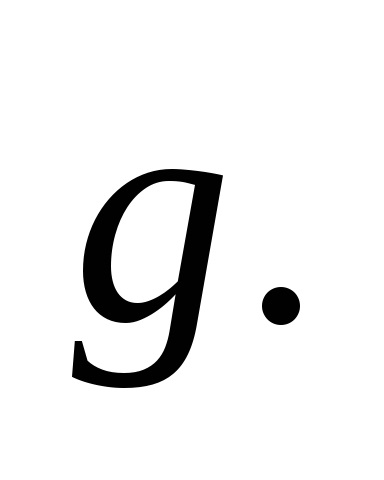
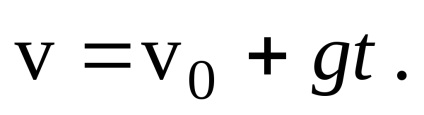
Gasim proiectiile vectorului de viteza pe axele de coordonate, care au proiectat aceasta ecuatie pe axele x si y:
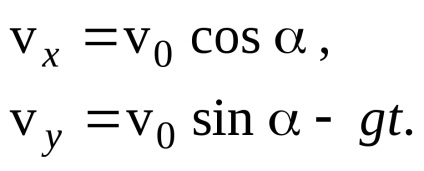
Din relația dintre modulul unui vector și proiecțiile sale pe axele carteziene, obținem:
b) Dacă este unghiul dintre vectorul de viteză și axa orizontală la un moment dat t1. atunci:
c) Scriem legea mișcării corpului în formă vectorică, ținând seama de faptul că în momentul inițial, corpul era la originea coordonatelor.
aici
Proiectăm această ecuație pe axa y:
Gasim timpul de zbor al corpului T din conditia ca in acest moment coordonata y = 0:
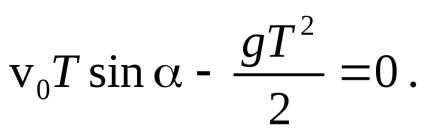
Una dintre rădăcinile ecuației T1 = 0 corespunde poziției inițiale a corpului, cealaltă rădăcină dă timpul de zbor al corpului:
d) Proiectăm ecuația (1) pe axa x:
Să găsim domeniul de zbor al corpului L din condiția L = x (T):
Pentru a determina înălțimea maximă de ridicare H., găsim timpul de zbor al corpului la cel mai înalt punct al traiectoriei de la condiția că în acest moment vectorul de viteză

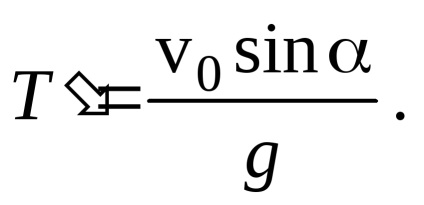
Rețineți că timpul de creștere T este egal cu jumătate din timpul de zbor. În consecință, timpul de creștere este egal cu timpul de coborâre.
e) Legea mișcării în forma coordonată, definită prin relațiile (2) și (3), definește esențial ecuația traiectoriei prin parametrul t. Excludând acest parametru, obținem ecuația traiectoriei într-o formă explicită:
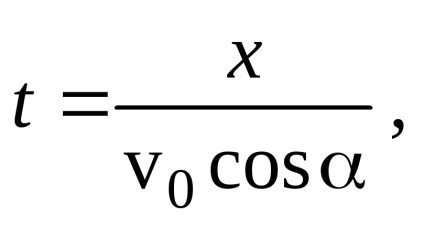
Rezultă din (4) că traiectoria unui corp turnat la un unghi față de orizont este o parabolă ale cărei ramuri sunt direcționate în jos (coeficientul x 2 este negativ). Parabola trece prin origine (una dintre rădăcinile ecuației y (x) = 0 este zero).
2. Aeronava zboară la o înălțime de h = 500 m de-a lungul unei linii drepte orizontale cu o viteză v0 = 100 m / s. Pilotul trebuie să lase bomba în țintă, care se află în fața aeronavei. La ce unghi a verticalei, ar trebui să vadă țintă în momentul căderii bombei?
P
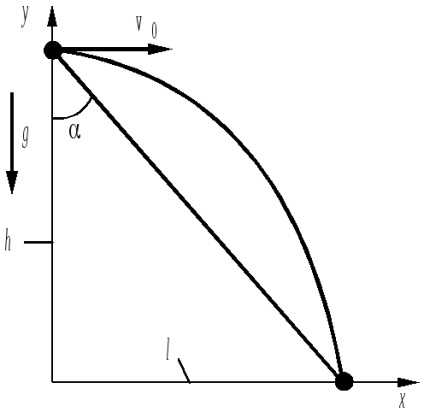
Unghiul dorit este determinat de relația evidentă:
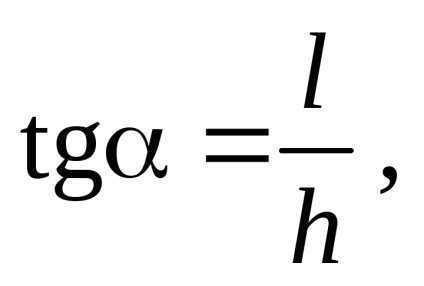
unde l este intervalul orizontal. Această valoare este egală cu t = v0t. unde t este timpul de zbor al bombei care se găsește din stare
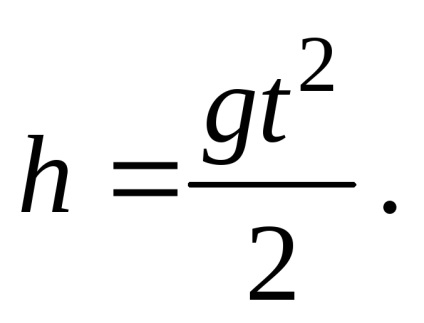
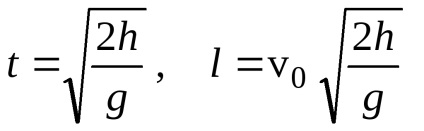
;
3. La ce unghi ar trebui aruncată piatra cu o viteză v0 = 20 m / s la care orizont ar trebui să zboare orizontal înainte de a cădea la pământ
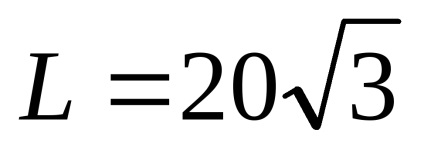
Soluția. Să scriem relația dintre intervalul de zbor. viteza inițială v0. unghiul și accelerația gravitației g (a se vedea (3) din problema 1 a acestei secțiuni):
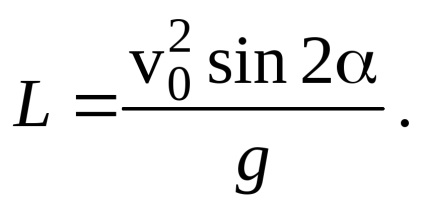
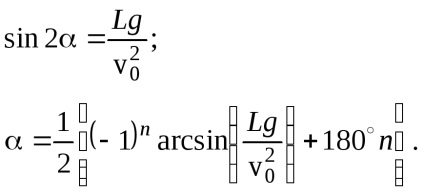
Aici n sunt numere întregi ale căror valori se găsesc din starea evidentă:
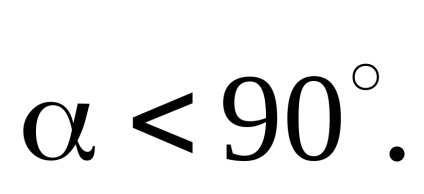
Fie n = 0. Atunci
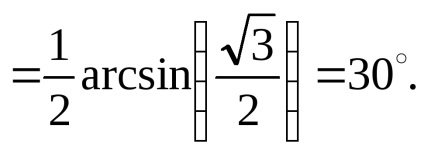
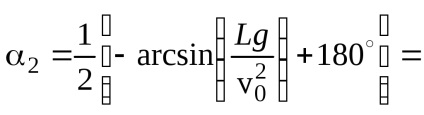
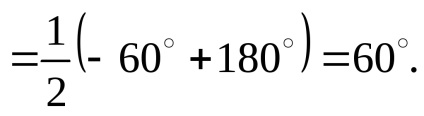
Pentru alte valori de n, unghiul este> 90. Deci, unghiurile cerute sunt:
4. Piatra a fost aruncată orizontal de la o înălțime mare la o viteză
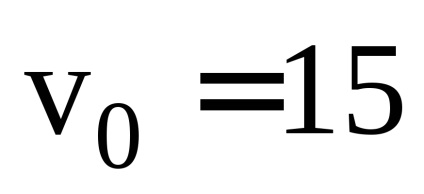
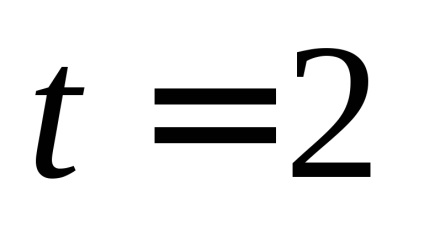
a) viteza


b) modulul vectorului de deplasare al pietrei.
Soluția. a) În conformitate cu expresia (1.12), viteza pietrei este
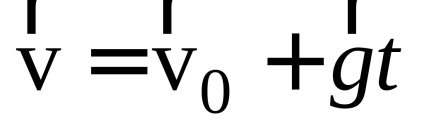
unde
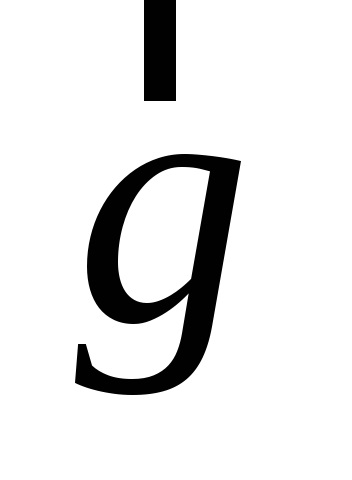
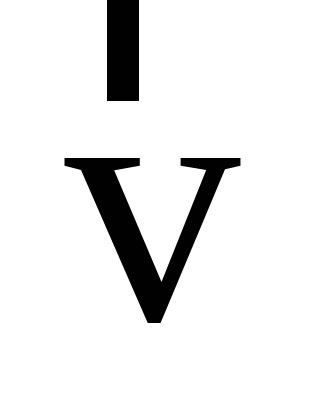
Prin definiție și
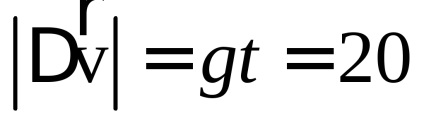
b) vectorul de deplasare este
,
unde