Scurtă descriere a documentului:
Demonstrația începe cu prezentarea temei lecției. Ecranul arată graficul funcției y = f (x). Graficul arată că nu există o tangență la grafic în punctul x = -1, iar la x = 0 linia tangentă este paralelă cu axa X. Apoi, se demonstrează definiția funcției minime a funcției. Afirmă că minimul funcției y = f (x) este x = x0. pentru care există un cartier, unde f (x)> f (x0) este valabil pentru toate punctele din vecinătate. Cu ajutorul cifrei se explică faptul că există o vecinătate x = 0 - de exemplu, (-0,5; 0,5), în care toate valorile cartierului satisfac starea f (x)> f (0). Se remarcă faptul că minimul unei funcții nu este cea mai mică valoare, deoarece se vorbește de cea mai mică valoare când se ia în considerare întregul domeniu al definiției. De multe ori vom face asta.
Mai departe, este prezentată o teoremă în care se dezvăluie relația dintre derivatul unei funcții și un extremum. Se remarcă faptul că dacă la un anumit punct al funcției există un extremum, atunci derivatul din acesta nu există sau este egal cu zero. Evident, atunci când investigăm o funcție, este necesar să găsim câteva puncte speciale. Se introduc conceptul de puncte staționare și critice. Punctele staționare sunt definite ca puncte care aparțin domeniului definiției funcției, cu un derivat egal cu zero. Punctele critice sunt punctele din domeniul definirii, unde funcția este continuă, dar derivatul nu există.
Se consideră un exemplu în care este necesar să se construiască un grafic al funcției y = -x 2 + 4x-1. Cunoscând caracteristicile grafului funcției patratice, putem spune imediat că graficul acestei dependențe este o parabolă cu ramificații orientate în jos, deoarece coeficientul de conducere al funcției este negativ. Punctul maxim al funcției este vârful acestei parabole. Tangenta la vârf este paralelă cu axa X, astfel încât condiția y = 0 este satisfăcută la vârf. Găsim derivația funcției y = (-x 2 + 4x-1) = -2x + 4. Rezolvând ecuația -2x + 4 = 0, obținem x = 2. În punctul x = 2, valoarea funcției y = 3. Punctul (2; 3) găsit este vârful parabolei. Pentru a construi parabola, sunt alese mai multe puncte simetrice, de exemplu (0; -1) și (4; 0). Acum este ușor să descrieți graficul acestei funcții.
Mai departe, se prezintă Teorema 2, în care sunt indicate suficiente condiții pentru extremum. În teoremă se indică faptul că pentru o funcție y = f (x) continuă pe intervalul X, care are în acest interval un punct critic x = x0. este adevărat:
- când există un cartier aproape de punctul critic, unde x<х0. f΄(x)<0, а для х>x0 f (x)> 0, atunci punctul este minimul funcției;
- când există un cartier aproape de punctul critic, unde x<х0. f΄(x)>0 și pentru x> x0 f (x) <0, то данная точка есть максимумом функции;
- când există un cartier aproape de punctul critic, unde semnul nu se schimbă atunci când trece printr-un anumit punct, atunci nu există nici un extremum.
În exemplul 2, este necesar să găsim extremumuri și să trasăm un grafic al funcției y = 3x 4 -16x 3 + 24x 2 -11. Mai întâi, se determină derivatul f (x) = (3x4 -16x3 + 24x2-11). După transformare, derivatul are forma f (x) = 12x (x-2) 2. Soluțiile ecuației sunt x = 0 și x = 2. Aceste puncte staționare sunt marcate pe linia numerică. De asemenea, pe linie, se observă care este funcția la fiecare dintre intervalele formate - creșterea sau scăderea. Este evident că pe intervalul (-∞, 0) funcția este în scădere, ca derivatul este negativ, și (0, 2) și (2; + ∞) derivat este pozitiv, funcția crește. La x = 0, funcția schimbă direcția de la scădere la creștere, acest punct este minim, semnul derivatului nu se schimbă la x = 2, deci nu există nici un extremum în ea. Gasim un punct minim f (0) = -11. În consecință, uinin. = -11.
Pentru a construi un grafic, este necesar să cunoaștem punctele critice staționare. Definim punctele de intersecție a unei funcții cu axele de coordonate - (-1; 0), (1; 0). Luăm în considerare faptul că se găsește minimul funcției (-11; 0). Și, de asemenea, punctul staționar (2; 5), unde tangenta este paralelă cu X este punctul de inflexiune. După găsirea mai multor coordonate de puncte, este construit un grafic al funcției.
Rezumând studiul, se construiește un algoritm pentru investigarea unei funcții continue arbitrare y = f (x). Algoritmul are 4 pași:
- căutați derivatul f (x);
- identificarea punctelor critice, staționare;
- construirea de puncte singulare pe linia de coordonate - critice și staționare, indicând semnul derivatului pe golurile care rezultă;
- concluzii despre monotonicitate, punctele extreme ale funcției.
Se face o remarcă separată cu privire la necesitatea marcării punctelor pe linia dreaptă de coordonate, care transformă numitorul formulei p (x) / q (x) la zero. Se indică faptul că aceste puncte nu sunt extreme.
În exemplul 3, este necesar să se investigheze funcția y = (x 2 -3) / (x 2 + 1). Funcția este examinată în conformitate cu algoritmul. Mai întâi, există derivatul f (x) = ((x 2 -3) / (x 2 + 1)) '. Folosind regula pentru găsirea derivatului unui coeficient, găsim derivatul f (x) = 8x / (x2 + 1) 2. Pe linia de coordonate, indicăm punctul în care derivatul este zero - x = 0. Apoi, aranjați semnele derivatului pe golurile formate. Evident, pe intervalul (-∞; 0) funcția scade și crește pe [0; + ∞). Judecând după proprietățile graficului, punctul x = 0 este minimul funcției, unde umin. = -3.
2. Puncte de funcționare extremum și căutarea lor
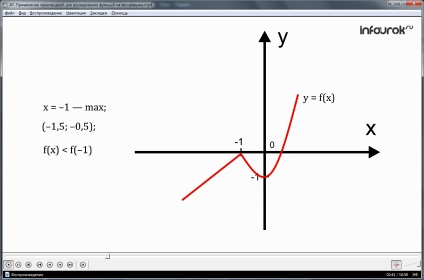
Luați în considerare graficul funcției din figura 1. Această funcție nu are tangent la punctul x = -1, iar la punctul x = 0, aceasta coincide cu axa y (adică, perpendiculară pe axa x).
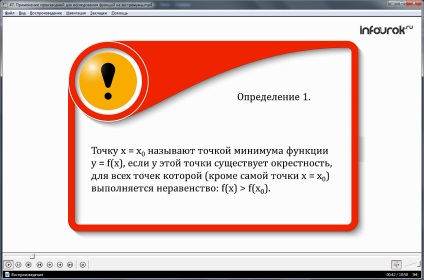
Definiție 1. Un punct x = x0 se numește un punct minim al funcției y = f (x) dacă acest punct are o vecinătate pentru toate punctele din care (cu excepția punctului x = x0 însăși), se menține următoarea inegalitate:
Aceasta este funcția al cărei grafic este prezentat în Fig. 1, are un punct minim x = 0. Deoarece la un anumit punct există un cartier, de exemplu, sau (-0,5; 0,5), pentru toate punctele, cu excepția punctului x = 0, f (x)> f (0). (ef de la X este mai mare de zero de la zero)
Valoarea funcției la punctul minim este ymin. (cel puțin un minim)
Notă. Dar această valoare nu este cea mai mică valoare a funcției, deoarece cea mai mică valoare este considerată în toate domeniile definiției, adică ymin diferă adesea de yname. (cel mai mic)
De exemplu, funcția a cărei funcție este prezentată în Fig. 1, nu are cea mai mică valoare, dar ymin (valoarea minimă) există.
Definiția 2. Punctul x = x0 se numește punctul maxim al funcției y = f (x) dacă acest punct are o vecinătate pentru toate punctele din care, cu excepția punctului x = x0. urmărește următoarea inegalitate: f (x) Să ne întoarcem la Figura 1, această funcție are un punct maxim x = -1. Deoarece la un anumit punct există o vecinătate, de exemplu (-1,5, -0,5), pentru toate punctele cu excepția punctului x = -1, f (x) Valoarea funcției la punctul maxim este ymax. (maxim iglok) Nu confunda această valoare cu yanibul. (cea mai mare sumă); cu cea mai mare valoare a funcției în întregul domeniu al definiției. Putem argumenta că cea mai mare valoare nu este prezentă în funcția în cauză, aymax (valoarea maximă) există. Punctele minime și maxime ale funcției sunt unite de termenul comun - punctele extreme (de la cuvântul latin extremum - "extreme"). Teoremă 1. Dacă funcția y = f (x) are un extremum la punctul x = x0. atunci la acest punct derivatul funcției este fie zero, fie nu există. Introducem o notație suplimentară: punctele din domeniul definirii unei funcții în care derivatul funcției este egal cu zero se numesc staționare. și punctele din domeniul definirii unei funcții în care funcția este continuă, dar derivatul funcției nu există, sunt critice. Exemplul 1. Construiți un grafic al funcției y = -x 2 + 4x-1. Soluția. Știți că graficul unei funcții patrate date este o parabolă, cu ramurile parabolei îndreptate în jos, deoarece coeficientul x 2 este negativ. Dar în acest caz vârful parabolei este punctul maxim al funcției, tangenta la parabola la vârful ei este paralelă cu axa x, astfel încât condiția y '= 0 trebuie îndeplinită la vârful parabolei. (bara punctată este zero) Avem: y '= (-x2 + 4x-1)' = -2x + 4. Ecuând derivatul la zero, obținem: -2x + 4 = 0; x = 2. Înlocuind valoarea x găsită în ecuația parabolei, obținem: y = -2 2 + 4 · 2 -1 = 3. (jocul este de trei) Astfel, vârful parabolei este punctul (2; 3), iar axa x este axa parabolei. Ca puncte de control, este convenabil să luăm punctul (0; -1) și simetric față de aceasta față de axa punctului parabolic (4; -1). În Fig. 2, o parabolă - un grafic al unei funcții cvadrate date este construit din cele trei puncte găsite. Teorema 2 (condiții suficiente pentru un extremum). Să presupunem că funcția y = f (x) este continuă pe intervalul X și are un punct staționar sau critic x = x0 în interiorul intervalului. apoi: a) dacă în acest moment există o vecinătate astfel încât pentru x<х0 выполняется неравенствоf´(х) <0, а при х>x0 este inegalitatea f (x)> 0, atunci b) dacă în acest moment există o vecinătate astfel încât pentru x<х0 выполняется неравенствоf´(х)>0, iar pentru x> x0 inegalitatea f (x)<0, то c) dacă acest punct are o vecinătate astfel încât semnele derivatului să fie aceleași atât la stânga cât și la dreapta punctului x0, atunci nu există nici un extremum în punctul x = x0. Exemplul 2. a) Găsiți punctele extreme ale funcției y = 3x 4 -16x 3 + 24x 2 -11; b) construi un grafic al acestei funcții. Soluția, a) Să găsim derivatul funcției date: f '(x) = 12х 3 -48х 2 + 48х f '(x) = 12x (x 2 -4x + 4); f '(x) = 12x (x-2) 2; Derivatul dispare în punctele x = 0 și x = 2 - acestea sunt două puncte staționare ale unei funcții date. În Fig. 3 semne derivate indicate schematic și domeniu intervalele comportamentale ale funcției: pe intervalul (-, 0) derivat este negativ, atunci funcția scade la intervale (0, 2) și (2 +) - creșteri ale funcției pozitive. Punctul, x = 0, este punctul minim al funcției și x = 2 nu este un punct extrem. La punctul minim x = 0 avem f (0) = -11 (înlocuim valoarea x = 0 în atribuirea analitică a funcției), apoi ymin = -11. b) Pentru a construi un grafic de funcții, trebuie să cunoașteți punctele critice grafică. Acestea includ: - punctul minim găsit (0; -1); - punct staționar x = 2; în acest punct f (x) = 3 · 2 4 -16 · 2 3 + 24 · 2 2 -11 = 5; - punctele de intersecție cu axele de coordonate; în acest exemplu, acesta este punctul (0; -11) deja găsit, punctul de intersecție a graficului cu axa y. Și din nou: puteți ghici că f (1) = 0, astfel încât punctul de intersecție a graficului cu axa x se găsește este punctul (1; 0). Deci, avem un punct minim (0; -11), punctul de intersecție a graficului cu Axa x este punctul (1; 0) și punctul staționar (2; 5). În acest moment, tangenta la graficul funcției este orizontală, dar acesta nu este punctul extrem, ci punctul de inflexiune. Graficul grafic al funcției este prezentat schematic în Fig. 4. Rețineți că există încă un punct de intersecție al graficului cu axa abscisă, dar nu am putut găsi. Studiat ca algoritm de generalizare.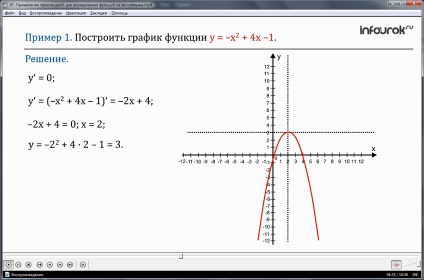
ALGORITMUL RESEARCH funcție continuă y = f (x) HA extremum monoton
1. Gasiti derivatul f '(x).
2. Găsiți punctele staționare și critice.
3. Marcați punctele staționare și critice de pe linia numerică și determinați semnele derivatului pe intervalele rezultate.
4. Bazându-ne pe teoreme, se pot trage concluzii despre monotonicitatea unei funcții și a punctelor extreme.
Notă: Dacă funcția dată este y = (y este de la Peh X împărțită ku X), apoi pe linia de numărul necesar de notat punctele în care numitorul q (x) este zero, pentru a determina derivatul de caractere. Dar aceste puncte nu sunt extreme.
Exemplul 6. Investigați funcția y = monotonicitate și extrema.
Soluția. Observăm că funcția este continuă peste tot, deoarece numitorul în orice punct x este mai mare decât zero. Folosim algoritmul de mai sus.
1) Să găsim derivatul unei funcții date:
(efectul ef de la X este egal cu opt X, împărțit la pătratul sumei de X pătrat și unul).
2) Derivatul dispare în punctele x = 0, acesta este un punct staționar. Derivatul există pentru orice puncte critice x și nu există puncte de discontinuitate a funcției.
3) Notați punctul 0 de pe linia numerică și aranjați semnele derivatului pe intervalele rezultate (figura 5).
4) Se trage concluzii: pe raza (-, 0) funcția scade, pe raza [0, +) funcția crește.
În plus, x = 0 este punctul minim, cu ymin = -3 (valoarea minimă este minus trei) (valoarea substituită x = 0 în formula y =).