În studiile anterioare am rezolvat inegalitățile trigonometrice de următoarele tipuri:
În această lecție rezolvăm inegalitățile de formă tan> a.
Vom folosi următorul algoritm de decizie (ca în lecția anterioară):
1. Dacă argumentul este complex (diferit de x), înlocuiți-l cu t.
3. Gasiti intervalul valorilor t. la care tangentoidul este situat deasupra liniei drepte y = a. Limita stângă a acestui interval este arctg a. și cea dreaptă întotdeauna (π / 2)
4. Notați dubla inegalitate pentru argumentul t. ținând cont de cea mai scurtă perioadă de tangență T = π (t va fi între abscisele arctg a și (π / 2)).
5. Facem o substituție inversă (revenim la argumentul original) și exprimăm valoarea lui x din dubla inegalitate, scriem răspunsul sub forma unui interval numeric.
Împărțim ambele părți ale inegalității cu 3. Să schimbăm variabila la t. Apoi, obținem o inegalitate mai simplă.
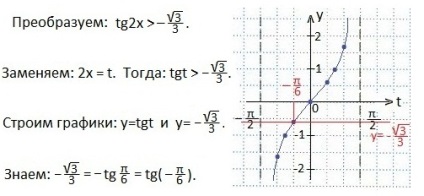
Definiți intervalul valorilor variabilei t. sub care inegalitatea este adevărată. Acestea sunt abscisele acelor puncte ale graficului funcției y = tan t. care se află deasupra liniei drepte. Vom afișa aceste valori ale lui t prin ecloziune. Scriem valorile găsite ale argumentului t ca o dublă inegalitate.
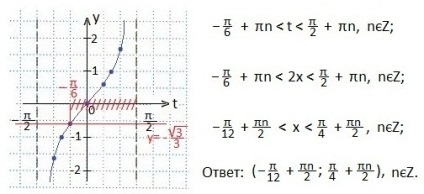
Transformăm partea stângă a inegalității cu formula tg (α + β) și obținem o inegalitate mai simplă. Facem o schimbare a variabilei.

Determinați intervalul dorit de valori ale variabilei t. Apoi exprimați x și scrieți răspunsul sub forma unui decalaj. Luăm în considerare faptul că inegalitatea nu este strictă, dar că nu există nici o tangență (π / 2).

Aplicăm regula pentru formulele de reducere:
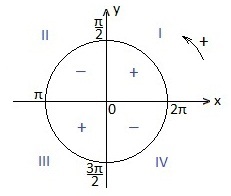
Argumentul nostru este în trimestrul 3, iar cotangentul în trimestrul al treilea are un semn plus. prin urmare, semnul funcției reduse nu se schimbă. Înregistrarea acestui argument (π / 2) este luată de 3 ori (un număr impar), deci funcția cotangent va fi schimbată în co-funcția - tangentă.
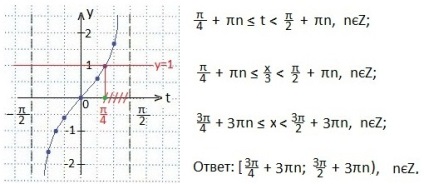
Acum, inegalitatea dată a luat forma: tgt≥1. Construim grafice ale funcțiilor y = tgt și y = 1. Definiți intervalul valorilor argumentului t. sub care inegalitatea tgt≥1 este adevărată. Răspunsul este scris sub forma unui decalaj. Inegalitatea nu este strictă, dar sfârșitul drept al intervalului nu intră în soluția inegalității, deoarece nu există nici o tangență (π / 2).
Dragi prieteni! Am rezolvat inegalitățile cu tangenta într-un mod grafic, dar, desigur, există o soluție mai scurtă - prin formule.
Dacă tgt Dacă tan> a. apoi arctg a + πn Aflați aceste formule și veți rezolva inegalitățile trigonometrice cu tangență mai rapidă! Pagina 1 din 1 1Articole similare