. 10 -5 s -1 - modulul vitezei unghiulare de rotație a Pământului,
vector al accelerației aparente a elicopterului în SC orizontal;
vectorul accelerației gravitaționale, calculat prin formula:
- vectorul de accelerație al forței gravitaționale în proiecția pe axa SC orizontală [7.5]:
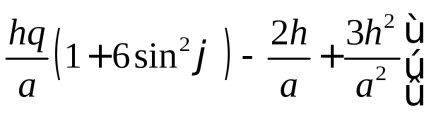
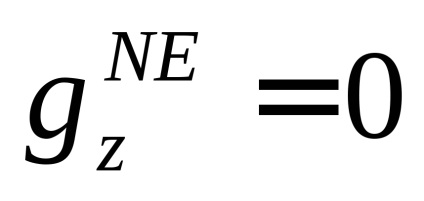
termenul datorat influenței potențialului centrifugal;
Mișcarea unghiulară spațială a elicopterului față de centrul de masă este descrisă de următoarele ecuații în proeminențele de pe axa cuplului SC:
În aceste ecuații:
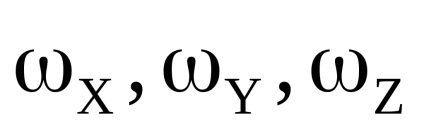

- componente ale vectorului momentului total
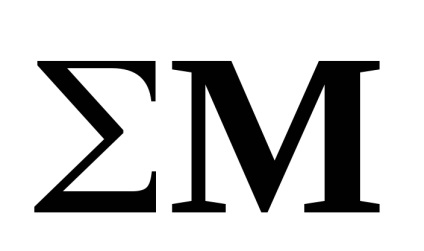
Pentru componenta de calcul a accelerației aparentă și accelerația unghiulară absolută a elicopterului CK legat a fost utilizat sub sistemul (7.10), liniarizată în apropierea așa-numita echilibrare ecuațiile traiectoriei cu coeficienți ce depind de viteza de zbor [7,4] suplimentata termeni neliniare în ecuațiile de forțe permite mai schimbarea unghiurilor de smoală și rola (așa-numitul „sistem parțial liniarizat“). Sistemul de ecuații scrise în axa asociată și este proiectat, așa cum sa menționat mai sus, pentru studiul condițiilor de zbor cu valori ale vitezei schimba de la 0 la maximum:
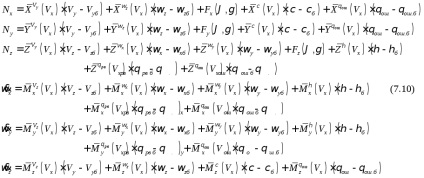
Nx. Ny. Nz - proiecții ale accelerației aparente pe axa cuplului SC;
Vx. Vy. Vz - proiecția vitezei elicopterului pe axa SC legat;
Vxb. Vyb. Vzb - proiecția vitezei elicopterului pe axa SC asociat pentru traiectoria de echilibrare;
x, y, z - proiecțiile vitezei unghiulare absolute a elicopterului pe axa SC asociat;
xb, yb, zb - proiecții ale vitezei unghiulare absolute a elicopterului pe axa SC asociat pentru traiectoria de echilibrare;
, , - Unghiuri Euler de orientare a elicopterului (pitch, roll, roll);
o.sh. - etapa generală a șurubului;
о.ш.б - pasul general al șurubului pentru traiectoria de echilibrare;
r.v. - pasul șurubului de direcție (în cazul unei scheme cu șurub de direcție);
r.v. - pasul șurubului de direcție (în cazul unei scheme cu un șurub de direcție) pentru o traiectorie de echilibrare;
este unghiul de deviație longitudinală a plăcii de vârf;
b - unghiul de deviere longitudinală a plăcii de înclinare pentru traiectoria de echilibrare;
este unghiul abaterii transversale a vârfului;
b este unghiul abaterii transversale a plăcii de înclinare pentru traiectoria de echilibrare;
- derivații proiecției forței aerodinamice pe axa X a SC cuplat pe parametrii de mișcare și control;
- derivatele proiecției forței aerodinamice pe axa Y a cuplatului SC asupra parametrilor de mișcare și control;
- derivații proiecției forței aerodinamice pe axa Z a SC cuplat la parametrii de mișcare și control;
- derivații proiecției momentului aerodinamic pe axa X a SC cuplat pe parametrii de mișcare și control;
- derivatele proiecției momentului aerodinamic pe axa Y a SC cuplat la parametrii de mișcare și de control;
- derivații proiecției momentului aerodinamic pe axa Z a SC cuplat la parametrii mișcării și controlului;
Ecuațiile (7.10) se obțin prin extinderea seriilor de relații Taylor pentru forțele și momentele care acționează asupra elicopterului în vecinătatea traiectoriilor de echilibrare. Aici, prin echilibrare înțelegem setul de traiectorii obținut ca rezultat al rezolvării sistemului de ecuații de statică, adică la momente aerodinamice zero și la unghiul de alunecare zero [7.4].
Pentru a reduce erorile dinamice care apar atunci când sunt utilizate ecuațiile (7.10), adică erorile cauzate de prezența reticulare, a termenilor neliniare Fx (, ), Fy (, ), Fz (, ) a introdus corectat pentru unghiul de influență ryskanya [7.3]. Pentru a elimina erorile dinamice cauzate de fenomene tranzitorii la schimbarea modurilor de echilibrare, interpolarea datelor din tabel utilizând o interpolare spline, care aproximează tabelul original sistemul B-spline [7.6] satisface cerința soluțiilor de continuitate în C 1.
A fost utilizată următoarea tehnică de aproximare. Curba construită pe baza bazei B-spline este descrisă după cum urmează [7.6]:
unde
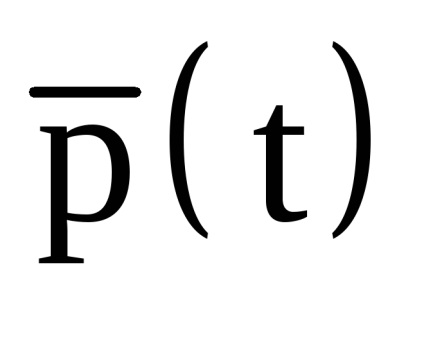

Nik (t) este funcția de greutate a B-splinei normalizate i-a unei curbe de bază a ordinului k (adică a gradului k-1) dată de relațiile de recurență:
Aici, xi sunt elementele vectorului nodului, iar t este parametrul care variază de la 0 la tmax = (n-k + 2).
vector nodular de lungime (n + k + 1), este introdus în considerare pentru propriile lor curbură curbe B-spline și este secvența de numere întregi non-descreștere - nodurile parametrice. vectorul nodular determinat de numărul de puncte înscrise în linia poligonală aproximate, ordinea curbei, și prezența (multiple) site-uri complexe.
Cunoscut [7.6] că curba B-spline este un polinom de grad (k-1) pe fiecare interval (xi, xi + 1) și toți derivații ei (k-2) th ordin sunt continue de-a lungul întregii curbă, această curbă este o funcție spline a ordinului k.
Astfel, ca urmare a utilizării sistemului B-spline în aproximarea datelor tabulare, este posibil să se asigure o tranziție continuă de la un mod de echilibrare la altul și să se elimine practic erorile dinamice rezultate.
Compoziția perturbațiilor afara partea dreaptă a ecuației (7.10). Este necesar să se includă sarcină aerodinamice suplimentare care rezultă datorită efectelor de vânt și este un factor major în descrierea mișcării necontrolate a elicopterului. Perturbațiile introduse de vânt duc la o schimbare în vectorul vitezei de zbor a elicopterului și, în consecință, la o schimbare a unghiurilor de atac și alunecare. Aceasta, la rândul său, conduce la modificările corespunzătoare ale coeficienților forțelor și momentelor aerodinamice necesare pentru calcularea componentelor accelerației aparente și a accelerației angulare absolute a elicopterului în SC asociat. Modelul condus nu abordează efectele asociate cu palete de elice curbe purtătoare și de a schimba eficiența aerodinamică, precum și formarea de turbionare suplimentar curge din cauza complexității acestui fenomen, care necesită o analiză suplimentară.
În general, ținând cont de influența vântului, vectorul de viteză este scris ca:
VB - vector de viteză a aerului cu mișcare neperturbată (pentru un elicopter coincide cu vectorul de viteză într-un SC geografic);
WB - vector al vitezei vântului.
În cadrul acestui model, vântul este considerat o rușine orizontală deterministă, adică se presupune că nu există deplasări verticale ale masei de aer; valoarea absolută a vitezei depinde de înălțimea și coordonatele geografice ale punctului, iar direcția este caracterizată prin unghiul azimutului, adică direcția vântului în raport cu direcția spre nord.
În studiul zborului unui elicopter de joasă altitudine, se folosesc două abordări pentru a forma caracteristicile necesare ale unui vânt plat:
Vântul constant, la care modulul de viteză este setat explicit (
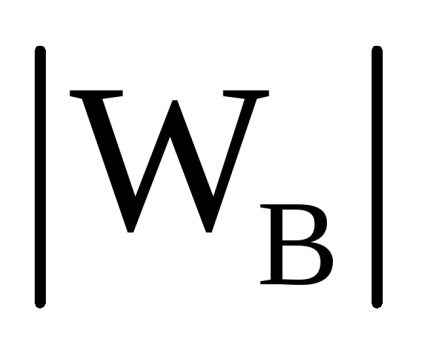
Vântul de-a lungul profilului, când valoarea absolută a vitezei vântului și a unghiului azimutului este determinată prin aproximarea profilurilor vitezei vântului, date a priori (figurile 7.7-7.8).
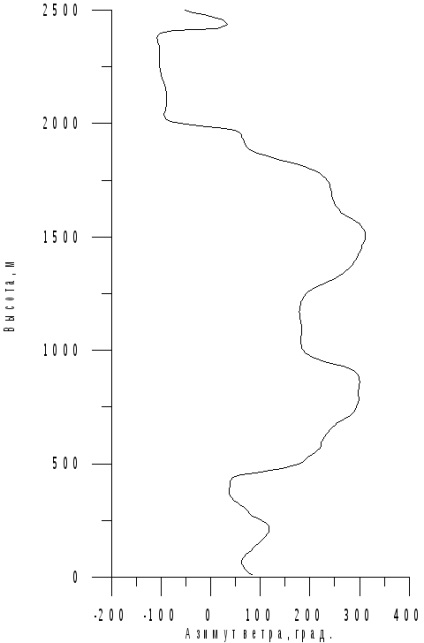
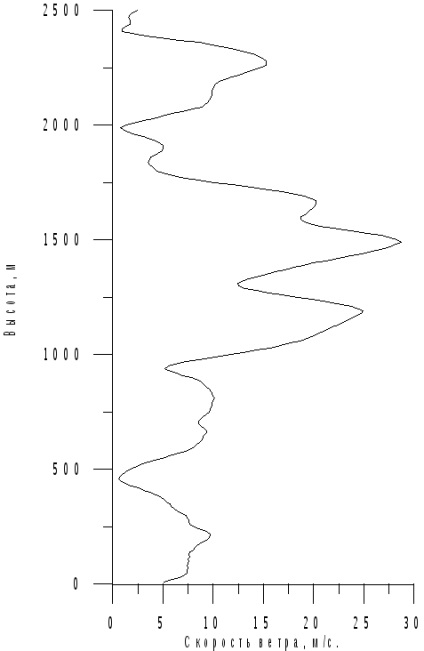
Apoi, vectorul de viteză a vântului rezultat în SC geografic este proiectat în SC asociat, unde, însumând cu vectorul total al vitezei elicopterului, formează vectorul de viteză a aerului (7.12).
Deoarece raportul pentru a calcula componenta de accelerare aparentă și accelerația unghiulară absolută a elicopterului este înregistrată în CK legat, tulburările contabile provocate de vânt, se realizează prin schimbarea coeficienților forțelor aerodinamice prin utilizarea, în raport argument modulul de viteză a aerului CS:
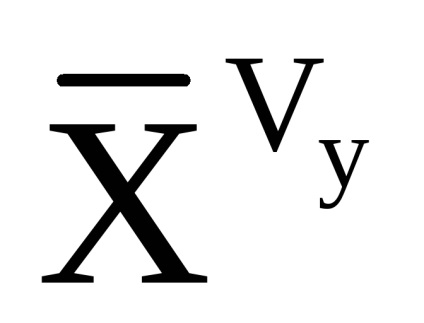
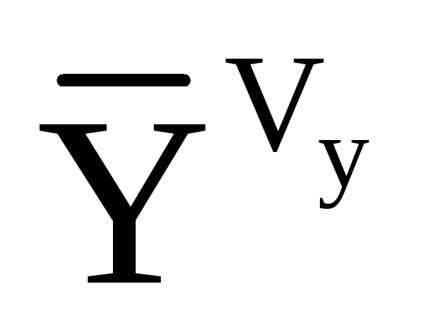
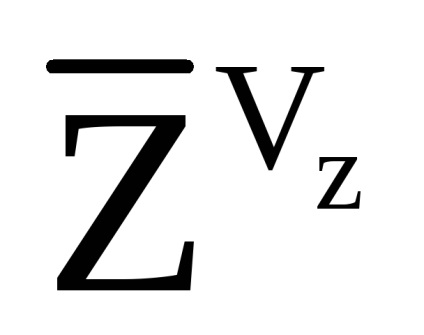
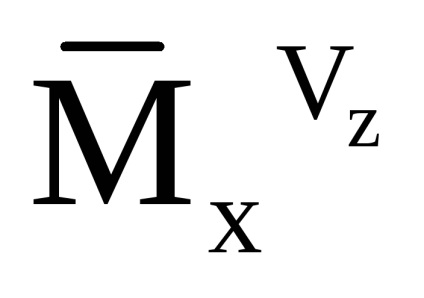
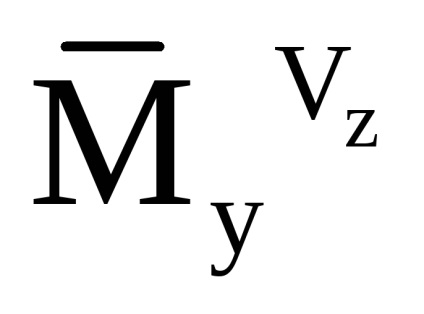
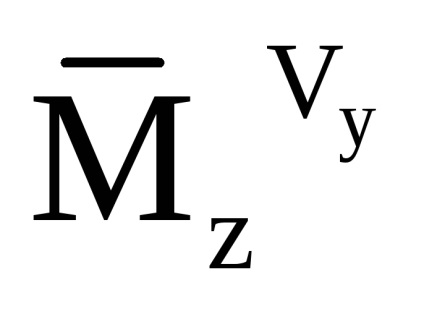
Pentru a recalcula accelerația aparentă în SC orizontală, se folosește următoarea relație:
- vector al accelerației aparente a elicopterului în SC cuplat, calculat folosind (7.10).
Matricea de tranziție de la gorizontnoy referitoare la SK determinat folosind parametrii Rodrigues-Hamilton [7,2]. Această abordare se bazează pe reprezentarea unui corp rigid finit rotație proprie în ceea ce privește transformarea quaternion sisteme ale căror componente au fost numite parametri Rodrigues-Hamilton de coordonate.
Comparativ cu ecuațiile cinematice clasice folosesc quaternions permite obținerea de înaltă precizie soluție stabilă numerică, lipsită de puncte singulare și asigurarea ortogonalitatea reciproce a axelor la coordonatele calculate:
unde q1. q2. q3. q4,

Ecuațiile cinematice în acest caz sunt scrise în formă vectorială [7.2]:
unde "

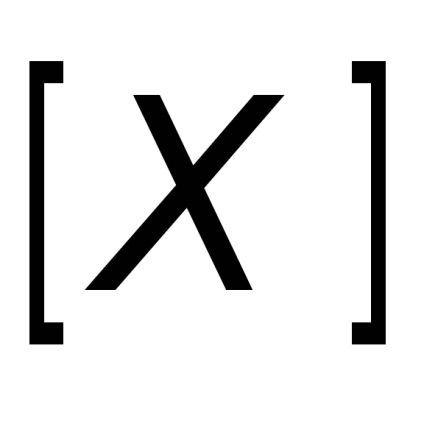
Unghiurile Euler tradiționale (, , ) pot fi determinate pe baza matricei de tranziție
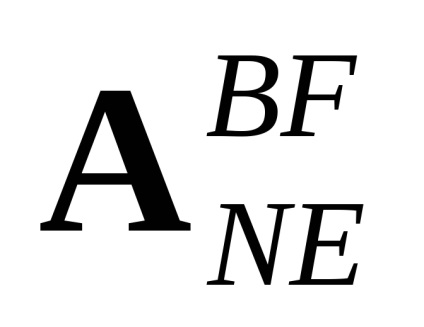
unde aij sunt componentele matricei
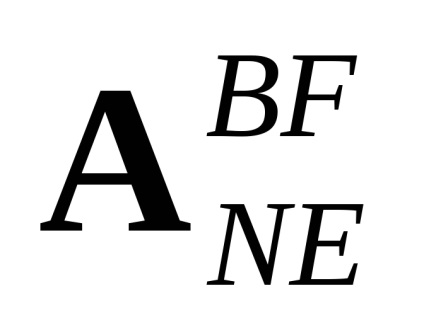
Astfel, un sistem complet de ecuații diferențiale parțial liniarizat în vecinătatea căii de echilibrare și descrie mișcarea spațială a elicopterului, cuprinde o Ecuațiile de mișcare 6 cm (7.7) și ecuația calcularea componentelor vectorului accelerației aparente și accelerația unghiulară a sistemului de formare a elicopterului (7,10), corelarea Ecuații aparente accelerare în CS geografic (7,11) și patru ecuații cinematic (7,15) care descrie dinamica schimbărilor parametrilor Rodrigues-Hamilton.