Le putem scrie în formă matricială:
- matrice de conformitate (matrice pătrată de dimensiune (6x6);
() sunt elemente ale matricei de conformitate.
Matrice de conformitate # 916; descrie fără ambiguități și complet caracteristicile de rigiditate ale elementului elastic considerat (în acest caz, tija).
Elementul matricei de conformitate () este o cantitate numeric egală cu deplasarea în direcția a, sub acțiunea forței unitare în direcția:
- Elementele diagonale caracterizează conformitatea tijei în direcția forței care acționează;
când - aceste elemente caracterizează conformitatea liniară a tijei (dimensiunea elementelor [m / H]);
la - aceste elemente caracterizează conformitatea unghiulară a tijei (dimensiunea elementelor [1 / mN]);
la. și când. - aceste elemente caracterizează legăturile încrucișate între deplasările unghiulare și liniare ale polului (dimensiunea elementelor [1 / H]).
Integratul moral, care descrie deplasarea () unui punct arbitrar al unei tije elastice sub acțiunea unei sarcini externe,
unde - forțele interne corespunzătoare care decurg din acțiunea sarcinii externe;
() - forțele interne corespunzătoare care decurg din acțiunea în pol a unei singure sarcini ().
Pe baza integralului Moore și a expresiei (1.5), vom scrie formula pentru determinarea elementelor () matricei de conformitate:
Conform expresiei (1.6), este evident că ().
Revenim la expresia (1.4):
Înmulțiți părțile stângă și dreaptă ale expresiei (2.1) cu
Apoi, indicând matricea de rigiditate, obținem ecuația de echilibru în forma matriceală
Aici este minorul matricei (determinant al submatricei, care este obținut din această matrice ștergând rândul i și coloana a).
Exemplu de calcul al matricei de conformitate a tijei rectilinii:
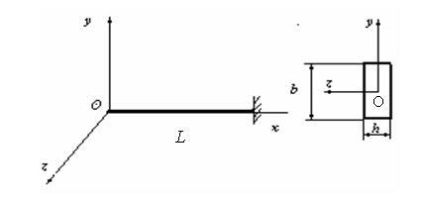
În cazul în cauză
1. Luați în considerare cazul când i = 1.
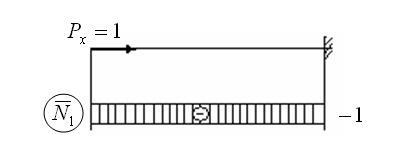
2. Luați în considerare cazul când i = 2
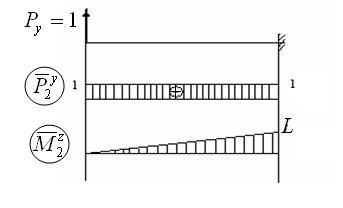
3. Considerăm cazul în care i = 3:
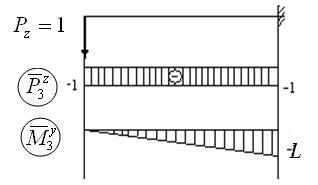
4. Luați în considerare cazul când i = 4:
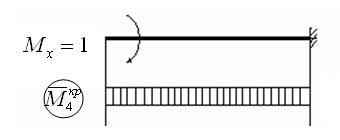
5. Luați în considerare cazul în care i = 5:
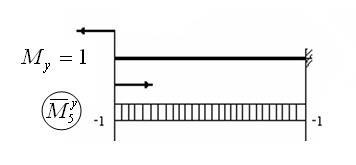
6. Luați în considerare cazul când i = 6:
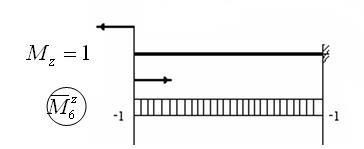
Apoi, conform formulei (1.6), obținem:
Să considerăm matricea de conformitate a unui element elastic rectiliniu având o secțiune cu o lungime variabilă. Elementul elastic este format din două secțiuni: M și E.
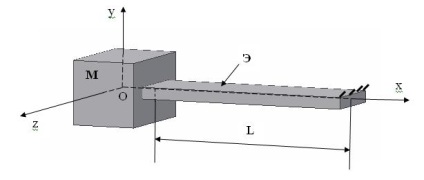
Considerăm matricea de conformitate în sistemul de coordonate Oxyz.
- aria secțiunii transversale a masei inerțiale;
- aria secțiunii transversale a elementului elastic;
Să luăm în considerare câteva proprietăți ale funcțiilor parțiale și ciudate.
1) Dacă A (x) este o funcție exactă, adică A (x) = A (-x) (de exemplu, A (x) = x 2).
2) Dacă A (x) este o funcție ciudată, adică A (x) = -A (-x) (de exemplu, A (x) = x),
Dacă așezăm polul în mijloc (;) al tijei, atunci, folosind proprietatea unei funcții ciudate, putem scrie
Aceasta înseamnă că dacă tija dreaptă are o secțiune transversală constantă de-a lungul lungimii tijei, iar polul este situat în mijloc și este conectat rigid la capătul liber al tijei, atunci matricea de conformitate are o formă diagonală.
În cazul unei matrice de conformitate diagonală, avem deplasarea polului numai în direcția acțiunii forței.
Pentru elementele elastice de secțiune transversală constantă, în cazul dispunerii polului într-un punct care coincide cu centrul tijei nedeformate, obținem:
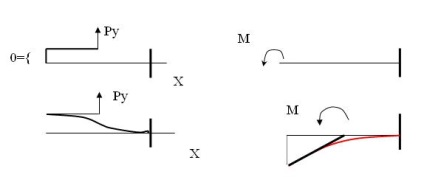
Un sistem de coordonate în care matricea de conformitate a unui element elastic are o formă diagonală se numește un sistem de coordonate normale.
În sistemul de coordonate normale sub acțiunea forței generalizate în pol, deplasarea are loc numai în direcția acțiunii forței
Definim elementele matricei de conformitate a RE a unei secțiuni constante într-un sistem de coordonate în raport cu axele și în centrul cărora RE are simetrie.
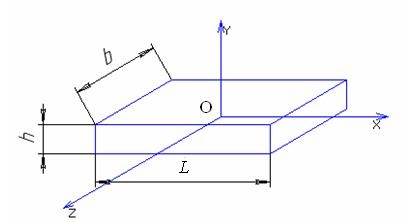
Pentru o anumită UE, matricea de conformitate va avea o formă diagonală.