Textul de mai jos face parte din cartea "Primul pas în realitatea cuantică".
4. Generalizarea funcțiilor trigonometrice în cazul oricărui unghi.
Verificați-vă că tot ceea ce sa spus mai sus despre funcțiile trigonometrice este valabil pentru situația descrisă în figură:
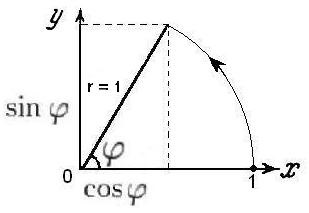
- vârful unghiului φ al triunghiului dreptunghiular coincide cu originea,
- ipoteza triunghiului, care este și raza cercului, este egală cu unitatea, r = 1,
- cosinusul este proiecția razei pe axa x,
- Sinusul este proiecția razei pe axa de coordonate.
Toate acestea sunt corecte, dar până acum numai pentru unghiuri acute, atunci când raza-hypotenuse este în primul trimestru.
Generalizarea situației în cazul oricărui unghi urmează în mod evident din figură:
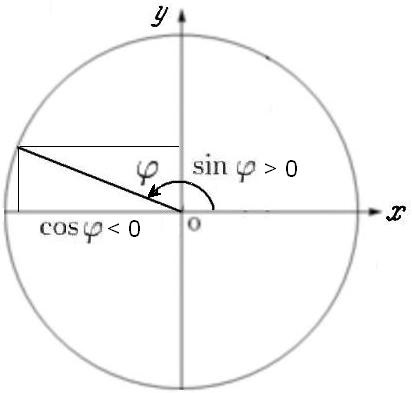
Și anume, pentru orice cosinus unghi, - unitatea de proiecție raza pe axa orizontală (O x), o condiție sine - unitate raza de proiecție pe axa verticală (O y), în plus, în acele cazuri în care proiecția intră în regiunea negativă a axelor de coordonate, semnul funcțiilor atribuite minus.
Toate celelalte funcții trigonometrice sunt exprimate în termeni de sinus și cosinus, formulele corespunzătoare sunt date mai sus.
Cele mai importante proprietăți și grafice ale funcțiilor trigonometrice
Funcția f (x) se spune că este chiar dacă f (-x) = f (x) și ciudată dacă f (-x) = -f (x).
Graficul unei funcții uniforme este simetric în raport cu axa ordinii (O y), iar graficul unei funcții ciudate este simetric în raport cu originea. Graficele arată că cosinusul este o funcție uniformă, iar sinus, tangent și cotangent sunt ciudate.
Cele mai multe funcții nu sunt nici chiar și nici ciudate, ele sunt suma a doi termeni:
Primul termen este partea parțială, al doilea termen este partea ciudată.
Dar funcțiile trigonometrice de bază au, așa cum am văzut acum, o paritate foarte clară.
5. Ce este necesar să vă amintiți despre funcțiile trigonometrice.
Mai întâi, o definiție generalizată a sinusului și cosinusului.
Aceasta implică imediat că, de exemplu, în al patrulea trimestru al cosinusul este sine pozitivă și negativă sau sinusoidală 180 ° este zero și cosinusul este egal cu unu minus. Și așa mai departe.
De asemenea, este util să fie în măsură să atragă grafice de sinus, cosinus, tangentă și cotangentă cu indicarea obligatorie a valorilor pe x și y-axe, așa cum se arată în figurile prezentate în tabel.
Formule foarte importante:
Ultimele două formule pot fi ușor reconstruite din ecuația:
În plus, este util să ne amintim paritatea-ciudățenia funcțiilor trigonometrice și să cunoaștem perioadele lor.
Formulele de convoluție sunt, de asemenea, utile, care ne permit să exprimăm valorile funcțiilor trigonometrice pentru orice unghi prin valorile funcțiilor trigonometrice ale unghiurilor primului trimestru.
Pentru a evita necesitatea utilizării unor astfel de calcule, aplicați regula mnemonică:
1. Dacă funcțiile trigonometrice ale unghiurilor sunt de 90 ° ± α sau 270 ° ± α. apoi modificările sine la cosinus, cosinus la sinus, tangent la cotangent, cotangent la tangent. În cazul unghiurilor de 180 ° ± α sau 360 ° ± α, funcțiile rămân neschimbate, adică sinusul rămâne un sinus, etc.
2. Semnul rezultatului este același ca și pentru funcția inițială din trimestrul la care unghiul inițial cade.
De exemplu: cos (180 ° - α) = - cos α.
Cosinul rămâne cosinus, deoarece 180 °, și nu 90 ° sau 270 °.
Unghiul inițial (180 ° - α) în al doilea trimestru, unde cosinul, funcția inițială, este negativ, deci semnul minus.
Aici, poate, asta e tot!
Uită-te la cât de multe formule trigonometrice în director! Dar aproape toate formulele de bază sunt ușor de obținut pentru una sau două acțiuni din acele relații pe care le-am luat în considerare.
Prin urmare, este mai simplu să nu învățați formulele trigonometrice, ci să ieșiți după cum este necesar.
Bineînțeles, nu ar face rău să cunoști trigonometria mai bine, dar aici este minimul necesar. Dacă este necesară citirea ulterioară, vor fi furnizate explicații suplimentare.