Criptografia cu cheie publică
Spre deosebire de cheia simetrică de criptare, nu găsim utilizarea istorică a criptografiei cu chei publice. Acesta este un concept relativ nou.
Criptografia simetrică este potrivită pentru organizații precum guverne, corporații militare și mari, implicate într-o legătură secretă.
Odată cu proliferarea mai multor rețele de calculatoare netestate în ultimele decenii, a fost simțită nevoia reală de a folosi criptografia la scară mai largă. Sa constatat că o cheie simetrică nu este practică datorită problemelor pe care le întâmpină pentru managementul cheie. Acest lucru a condus la o chestie deschisă de criptosisteme.
Procesul de criptare și decriptare este prezentat în următoarea ilustrație -
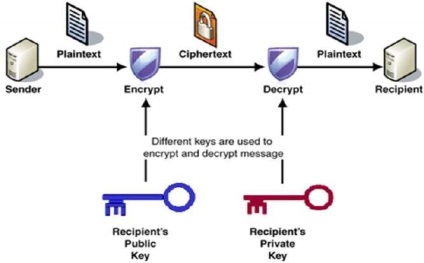
Cele mai importante proprietăți ale schemei principale de criptare publică -
Se utilizează chei diferite pentru criptare și decriptare. Această proprietate a setat această schemă diferită de schema simetrică de criptare.
Fiecare receptor are o cheie unică de decriptare, care se numește de obicei cheia privată.
Unele garanții ale autenticității cheii publice sunt necesare în acest sistem pentru a evita înlocuirea de către inamic ca receptor. În mod tipic, acest tip de sistem criptologic include o parte terță sigură, care certifică faptul că o anumită cheie publică aparține numai unei anumite persoane sau unei entități.
Algoritmul de criptare este suficient de complex pentru a interzice difuzarea de către cipher a textului deschis, din textul cipher și cheia de criptare (cheia publică).
Deși cheile private și publice sunt legate matematic, nu este posibil să se calculeze cheia privată din cheia publică. De fapt, partea intelectuală a oricărui sistem criptosomatic al cheii publice în proiectarea relației dintre cele două chei.
Există trei tipuri de scheme de criptare a cheilor publice. Le vom discuta în următoarele secțiuni -
RSA Cryptosystem
Acest sistem criptos este unul din sistemul original. Acesta rămâne cel mai ocupat sistem criptosist chiar și astăzi. Sistemul a fost inventat de trei oameni de științăRivest, Adi Shamir și Len Adleman și. prin urmare, se numește criptosistem RSA.
Vedem două aspecte ale sistemului de criptare RSA, generând mai întâi o pereche cheie și al doilea algoritm de criptare și decriptare.
Generarea perechii cheie RSA
Fiecare persoană sau parte care dorește să participe în legătură cu utilizarea criptării trebuie să genereze o pereche de chei, și anume o cheie publică și o cheie privată. Procesul urmat în generarea cheilor este descris mai jos -
Modul modul RSA (n)
Alegeți două mari numere prime p și q.
Calculați n = p * q. Pentru criptarea puternică incorectă, permiteți n cantități mari, de regulă, să nu fie mai mici de 512 biți.
Găsiți numărul (derivat f)
Numărul trebuie să fie mai mare de 1 sau mai mic. decât (p - 1) (Q - 1).
Nu ar trebui să existe un factor comun pentru e și (p - 1) (q - 1), cu excepția lui 1. Cu alte cuvinte, cele două numere e și (p - 1) (q - 1) sunt relativ prime.
Formularul cheie public
O pereche de numere (n, e) formează o cheie publică a RSA și este făcută publică.
Este interesant faptul că, deși n este parte a unei chei publice, dificultatea de a factoriza un număr mare prime asigură că un atacator nu poate găsi două prime numere la un timp finit (p Q) folosit pentru a obține n. Aceasta este puterea RSA.
Generarea unei chei private
Cheia privată d este calculată de la p, q, e. Pentru un n și e dat, există un număr unic d.
Numărul d este modulul invers (e - 1) (q - 1). Aceasta înseamnă că d este mai mică decât (p - 1) (Q - 1) astfel încât atunci când se înmulțește cu e, este 1 modulo (p - 1) (q - 1).
Această relație este scrisă matematic după cum urmează:
Algoritmul extins euclidian ia p, q, e și ca intrări și dă q ieșire.
Un exemplu de generare a perechilor de chei RSA este prezentat mai jos. (Pentru simplitatea înțelegerii, numerele prime p și q sunt luate aici ca valori mici. În practică, aceste valori sunt foarte mari).
Fie ca cele două prime să fie p = 7 și g = 13. Astfel, modulul η = PQ = 7 x 13 = 91.
Selectare e = 5, ceea ce este corect pentru acest lucru, deoarece nu există un număr care este un factor comun de 5 și (p - 1) (Q - 1) = 6 x 12 = 72 pentru 1, cu excepția.
O pereche de numere (n, e) = (91, 5) formează o cheie publică și poate fi pusă la dispoziția celor care doresc să ne trimită mesaje criptate.
Intrarea p = 7, g = 13 și e = 5 pentru algoritmul euclidian extins. Semnalul de ieșire va fi d = 29.
Asigurați-vă că d este evaluat corect prin calcul -
Prin urmare, cheia comună (91, 5) și cheile private (91, 29).
Criptare și decriptare
După generarea perechii de chei, procesul de criptare și decriptare este relativ simplu și ușor de calculat.
Este interesant de menționat că RSA nu lucrează direct cu șirurile de biți, ca în cazul cheii de criptare simetrice. Funcționează numerele modulo n. Prin urmare, este necesar să se reprezinte plaintext ca o serie de numere mai mici de n.
Criptare RSA
Să presupunem că expeditorul ar dori să trimită un mesaj text unei persoane a cărei cheie publică (n, e).
Apoi expeditorul este un text deschis ca o secvență de numere mai mici de n.
Pentru a cripta primul plaintext P, care este un numar modulo n. Procesul de criptare este un pas simplu matematic, cum ar fi -
Cu alte cuvinte, textul cifrat C este egal cu textul deschis P multiplicat de el însuși de e ori, și apoi restored modulo n. Aceasta înseamnă că C este, de asemenea, oarecum mai mică decât n.
Revenind la exemplul nostru de generare de chei cu plaintext P = 10, primim un C -
RSA decriptare
Procesul de decriptare pentru RSA este, de asemenea, foarte simplu. Să presupunem că destinatarul cheii publice a perechii (n, e) a primit C criptat.
Receptorul ridică C la puterea tastei sale secrete e. Rezultatul modulo n este textul simplu al lui P.
Revenind din nou la exemplul nostru numeric, textul cifrat C = 82 va fi decodificat la numărul 10, folosind cheia secretă 29 -
Analiza RSA
Securitatea RSA depinde de avantajele a două funcții separate. Sistemul de criptare RSA este cel mai popular sistem criptografic cu cheie publică a cărui putere se bazează pe dificultățile practice de a factoriza numere foarte mari.
Criptare O funcție este considerată ca o funcție unică de a converti textul în text criptat și poate fi doar anulată cu cunoașterea cheii secrete e.
generare cheie -. Dificultatea de a determina o cheie secretă a cheii publice RSA este echivalent cu factorizarea modulo n atacator, astfel, nu se poate utiliza cunoașterea cheii publice RSA pentru a determina cheia secretă RSA, în cazul în care nu se poate lua în considerare punctul Este, de asemenea, o funcție de una dintre modalitățile. , trecând de la valorile p și q modulo n este ușor, dar inversul este imposibil.
Dacă una dintre aceste două funcții nu este dovedită într-o singură direcție, RSA va fi ruptă. De fapt, dacă metoda de factoring se dezvoltă efectiv, RSA nu va mai fi sigură.
Rata de criptare RSA scade brusc din atacuri dacă numărul p și q nu sunt numere prime prime și / sau cheia publică e este selectată un număr mic.
ElGamal Cryptosystem
Împreună cu RSA, există și alte criptosisteme cu cheie publică. Multe dintre ele se bazează pe diferite versiuni ale problemei logaritmice discrete.
Sistemul cryptosystem ElGamal, numit Varianta curbei eliptice, bazat pe logaritmul discret al problemei. Aceasta derivă din prezumția că logaritmii discrete nu pot fi găsiți în termeni practici pentru un anumit număr, în timp ce o operație de putere inversă poate fi calculată eficient.
Să trecem printr-o versiune simplă a lui ElGamal, care funcționează cu un număr modulo p. În cazul variantelor curbei eliptice, se bazează pe sisteme de numere complet diferite.
Generarea perechilor de chei ElGamal
Fiecare utilizator ElGamal al sistemului de criptograme generează o pereche de chei în felul următor:
Alegerea unui număr mare mare p. În general, este selectat un număr prime între 1024 și 2048 de biți în lungime.
Selectarea elementului generator g.
Acest număr ar trebui să fie între 1 și p - 1, dar nu poate exista nici un număr.
Este generatorul grupului multiplicativ de numere întregi modulo p. Înseamnă. că pentru orice număr întreg m sunt coprime cu p, există un întreg k astfel. că rk = modul n.
De exemplu, 3 este un generator din grupa 5 (Z5 =).
Selectarea unei chei private. Cheia privată x orice număr mai mare de 1 sau mai puțin. decât P-1.
Partea computațională a valorii cheii publice y este calculată din parametrii p, r și cheia secretă x după cum urmează. -
Obținerea cheii publice. Cheia deschisă ElGamal constă din trei parametri (p, r, y).
De exemplu, să presupunem. că p = 17 și că r = 6 (Acest lucru poate fi confirmat prin faptul că 6 este un generator al grupului Z 17). Cheia secretă x poate fi orice număr mai mare de 1 și mai mic de 71, deci alegem x = 5. Valoarea y se calculează după cum urmează:
Astfel, cheia privată 62 și cheia publică (17, 6, 7).
Criptare și decriptare
Generarea perechii de chei ElGamal este relativ mai simplă decât procesul echivalent pentru RSA. Dar criptarea și decriptarea este un pic mai complicat decât RSA.
Criptarea ElGamal
Să presupunem că expeditorul dorește să trimită un text simplu unei persoane a cărei cheie publică ElGamal (p, r, y) și apoi -
Expeditorul este un text deschis sub forma unei serii de numere modulo p.
Pentru a cripta primul plaintext P, care este reprezentat ca un număr modulo p. Procesul de criptare pentru obținerea codului C este următorul:
- Alegeți în mod aleator numărul k;
- Se calculează cele două valori ale lui C1 și C2, unde -
-
Trimiteți textul criptat C, format din două valori separate (C1, C2) trimise împreună.
Dacă ne referim la exemplul nostru ElGamal de generare a cheii de mai sus, textul simplu P = 13 este criptat după cum urmează:
- Alegeți în mod aleatoriu o serie, să zicem, k = 10
- Se calculează cele două valori ale lui C1 și C2, unde -
-
Trimiterea textului criptat C = (C1, C2) = (15, 9).
Decriptarea ElGamal
Pentru a decripta criptatul (C1, C2) folosind cheia secretă x, următorii doi pași vor fi luați -
Calculați inversia modulară (C1) x modulo p, astfel încât (C1) -x, ca regulă. numit factor de decodare.
Obțineți text clar utilizând următoarea formulă -
În exemplul nostru, pentru a decripta textul criptat C = (C1, C2) = (15, 9) folosind cheia secretă x = 5, raportul de decriptare
Extrageți platextul P = (9 × 9) modulo 17 = 13.
Analiza ElGamal
În sistemul ElGamal, fiecare utilizator are o cheie secretă x. și constă din trei componente ale cheii publice - un modulo simplu p, un generator r și un public Y = r x Îți voi ajuta p. Puterea lui ElGamal se bazează pe complexitatea problemei logaritmice discrete.
Dimensiunea cheii protejate este de obicei> 1024 biți. Astăzi chiar 2048 de biți folosesc o cheie lungă. La viteza de procesare front-end, Elgamal este destul de lent, este utilizat în principal pentru protocoalele cheie de autentificare. Datorită eficienței de procesare mai ridicate, variantele eliptice ale curbei ElGamal devin din ce în ce mai populare.
Criptografia pe curbele eliptice (ECC)
Criptografia pe curbele eliptice (ECC) este un termen folosit pentru a descrie un set de instrumente și protocoale criptografice a căror securitate se bazează pe versiuni speciale ale problemei logaritmice discrete. Nu utilizează numerele modulo p.
ECC se bazează pe seturi de numere care sunt legate de obiecte matematice numite curbe eliptice. Există reguli pentru adăugarea și calcularea mai multor numere, la fel ca și pentru numerele modulo p.
ECC include variante ale mai multor scheme criptografice care au fost inițial dezvoltate pentru numere modulare, cum ar fi criptarea ElGamal și algoritmul de semnătură digitală.
Se crede că logaritmul discret este mult mai dificil de aplicat la punctele de pe o curbă eliptică. Aceasta induce o tranziție de la un număr modulo p la puncte pe o curbă eliptică. De asemenea, un nivel de securitate echivalent poate fi obținut cu tastele mai scurte dacă folosim variante eliptice ale curbei pe bază.
Tastele mai scurte duc la două avantaje:
- Confortul managementului cheie
- Calcul eficient
Aceste avantaje fac ca curba eliptică bazată pe opțiunile schemei de criptare să fie foarte atractivă pentru aplicațiile în care resursele de calcul sunt înghesuite.
Diagramele RSA și ElGamal - pentru comparație
Să analizăm pe scurt schemele RSA și ElGamal pe diferite aspecte.