Mecanisme Chebyshev Proiect propriu-rayutsya toate fur-închizători, set-Nye-Kim au fost matematician crescut-SEA-cer - Pafnuti Cebîșev (1821-1894).
Mathesis Editura Odessa "Mathesis" din 1904 până în 1925 a produs cărți surprinzător de interesante. Unii dintre ei au devenit clasici, unii dintre ei sunt uitați acum. Îi unește că toate sunt rarități.
V.O.F.E.M. Versiunea electronică a revistei științifice populare, care a stabilit tendința genului în literatură în limba rusă.
Dacă "ardeți" un CD sau DVD pe computerul dvs., porțiunea înregistrată a "martorului" pare mai întunecată decât cea neutilizată.
Ce este mai mult pe discul prezentat în imagine. - informații înregistrate sau spațiu liber?
În ceea ce privește matematica, ambele unități CD și DVD sunt un inel. Raza circumferinței interioare, care leagă cercul, pe care nu este scris nimic, este egală cu 2 centimetri. iar raza întregului disc standard este de 6 centimetri. Informația este înregistrată pe o pistă spirală, desfăcută de la un cerc mai mic la unul mai mare. Deoarece aceeași cantitate de informații corespunde cu aceeași lungime a liniei, cantitatea de informații înregistrate pe "martor" este proporțională cu aria ocupată de inel.
Să începem să "ardem" discul la fel ca un computer. Dacă lățimea inelului este egală cu lățimea înregistrată și cantitatea neînregistrat de 2 centimetri, este văzut. cât de mică este aria părții utilizate. În acest caz, chiar dacă zona în zona înregistrată a inelului pentru a adăuga toate cercul interior, pe care este scris nimic, suprafața totală a lor va fi în continuare mai mică decât cea a unei părți neînregistrat a „spațiile libere“.
Pentru ca exact jumătate din "martor" să fie ocupat, inelul interior trebuie să aibă o lățime de aproximativ 2,5 cm, iar inelul exterior este de aproximativ 1,5 cm.
De ce apare un astfel de efect?
În plan, mingea este un cerc și, prin urmare, volumul este zona acestui cerc. După cum știm cu toții, aria unui cerc de rază $ R $ este egală cu $ \ pi R ^ 2 $. Pentru a calcula aria inelului, este necesar din zona cercului mare de a deduce zona neutilizată mică - $ \ pi \ cdot (R ^ 2-r ^ 2) $. Și, din moment ce depinde de raza, dar încă într-un pătrat, apoi mai aproape de inelul rază mai mare a descris, mai mare, pentru aceeași lățime, contribuția sa la zona.
În spațiul nostru tridimensional, volumul unei sfere depinde de raza ridicată la a treia putere. Aceasta înseamnă că efectul în cauză devine și mai pronunțat: bóCea mai mare parte a volumului mingii este concentrată aproape de graniță!
Ce este mai mult pe volumul din coaja sau pulpa portocalie? Cojile ocupă un strat aparent nu foarte gros, dar se află lângă marginea mingii. Și volumul său în figura de mai sus este egal cu volumul întregii părți gustoase a portocalei. Cumparand o portocala cu o piele groasa, in volum obtineti practic o coaja.
Uite, de asemenea
Alte schițe din secțiunea "Piețe și volume" 4
Puzzle interactiv "Teorema lui Pitagora"
Frumoasă dovadă interactivă a teoremei pitagoreene.
Pătrat de figuri
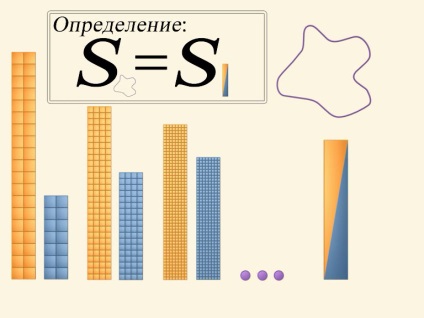
Pătratul pătratului este egal cu pătratul lungimii laterale. Este ușor să calculați aria unei figuri care se împarte în câteva pătrate. Și care este zona unei figuri delimitată de o curbă arbitrară?
Formula de vârf
Calculul interactiv al suprafeței poligonului pe care l-ați desenat.
Volumul mingii: baloanele Archimedes

Cilindrul având cel mai mare cerc de bază de minge, și înălțimea acestuia egală cu secțiunea transversală este, există o bonder bilă; și suprafața sa este o suprafață de o jumătate și jumătate a sferei. Arhimede