Pentru a determina coeficientul de frecare al odihnei, se folosește un tribometru, care permite numărarea unghiului de înclinare al planului-1 în mișcare față de planul orizontal-2. Tangenta unghiului este egală cu coeficientul de fricțiune al repausului la care corpul-3 plasat pe planul-1 începe să se miște. Unghiul este măsurat prin transportul-4.
Pentru a determina coeficientul de frecare cinematic, este necesară o instalație, dispozitivul fiind ușor de înțeles din figură (vezi figura 2.3). Corpul 2 se mișcă de-a lungul planului 1 sub influența tensiunii firului, aruncată prin blocul-4. Forța de tensionare este reglată prin modificarea greutății încărcăturii-3.
Forța de frecare este egală cu greutatea paharului cu sarcina, la care corpul-2 alunecă uniform pe suprafața -1
unde m este masa cuponului cu sarcina,
(ksk este coeficientul cinematic de frecare alunecare,
mm este masa corpului-2,
- accelerarea gravitației.
Rezolvarea ecuației (2.7) față de kc. avem
Încărcarea tepo-2, observăm că mișcarea sa are loc cu o masă mai mare de supraîncărcare impusă pe cupa-3. Dar raportul rămâne întotdeauna constant, egal cu coeficientul de frecare.
ORDINEA DE PERFORMANȚĂ
1. Setați unul din corpurile sugerate pe tribometru, ridicând încet planul-2, observați unghiul la care corpul începe să alunece,
2. Rulați măsurătorile de mai multe ori, scriind datele într-un tabel pregătit anterior 2.2.
3. Rotiți corpul într-un alt plan și repetați experimentul.
4. Să tragem o concluzie.
5. Aceste măsurători ar trebui făcute cu alte probe propuse de către profesor.
6. Se determină coeficientul de frecare al suportului pentru eșantioane cilindrice de același diametru, realizate din diferite materiale prin ecuația (2.4).
7. Comparați coeficienții de frecare alunecătoare și frecare de rulare pentru perechi identice de suprafețe de frecare.
8. Comparați coeficienții de fricțiune de odihnă și mișcare pentru perechi identice de suprafețe de frecare.
Determinarea coeficientului de fricțiune statică de alunecare
1. Construiți dependența forței de frecare de forța presiunii normale.
2. Din dependența obținută (grafic), determinați valoarea medie a coeficientului de frecare.
1. Care este forța de frecare? Cum este direcționată forța de frecare uscată către suprafața corpului?
2. Ce se numește frecarea de odihnă, frecare alunecoasă, frecare la rulare?
3. De ce depinde coeficientul de frecare?
4. Ce tipuri de frecare știți?
5. Care este unitatea pentru măsurarea coeficientului de frecare?
6. Care este valoarea coeficienților de frecare în agricultură?
7. Dați exemple de utilizare a forțelor de frecare în funcționarea mașinilor agricole.
8. Ce fel de frecare se numește intern?
9. Ce determină forța de frecare internă?
LUCRĂRI DE LABORATOR №3
INSPECȚIA LEGII DE BAZĂ A DINAMICII ROTAȚIEI
CIRCULAȚIE CU APLICAREA PENDULULUI TRANSFRONTALIER
Scopul lucrării este de a verifica fezabilitatea legii fundamentale a dinamicii mișcării de rotație.
Dispozitive și accesorii: pendulul lui Oberbek, un set de încărcături, un cronometru, etriere, riglă.
Legea de bază a dinamicii mișcării de rotație pentru un corp rigid complet după cum urmează: momentul de rotație al forței care acționează asupra unui corp este produsul dintre momentul de inerție al unui corp pentru accelerație unghiulară imprimată corpului, și este scris după cum urmează:
unde este cuplul forței rotative,
- moment de inerție a corpului,
- unghiul de accelerare a corpului.
Momentul inerției corpului este o măsură a inerției corpului și în cazul general este egal cu suma momentelor de inerție a punctelor sale materiale
- numărul de serie al punctului material, = 1,2,3, ......
Momentul de inerție a materialului față de o anumită axă de rotație este egal cu produsul din masa acestui punct de către pătratul distanței de la acest punct la axa de rotație
aici m este masa unui punct material,
r este distanța de la punctul material la axa de rotație.
Momentul forței este o cantitate vectorică al cărei modul este egal cu produsul forței pe braț
aici M este momentul forței,
F este forța care acționează asupra corpului,
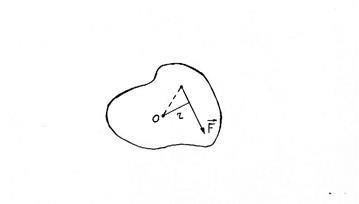
Momentul forței poate fi schimbat în două moduri: schimbarea forței de acțiune sau schimbarea umărului forței cu aceeași forță.
În lucrarea noastră vom schimba magnitudinea forței care acționează, lăsând umărul forței neschimbate.
Atunci când cuplul forței de rotație este schimbat la un moment constant de inerție a pendulului, accelerația unghiulară se va schimba. Dar raportul cuplului dintre forța rotativă și accelerația unghiulară va fi o valoare constantă egală cu momentul inerției pendulului.
La locul de muncă, este necesar să se verifice corectitudinea acestei declarații.
pendulului cruciform (vezi. Fig. 3.2.) este un disc cu armat -1 pe acesta la un unghi de 90 0 unul de celălalt prin patru tije lungi 2, care se pot deplasa sarcinile m0 masa -3 fiecare. Blocul 1 poate fi înfășurat -4 fire, al cărui capăt liber poartă greutatea încărcăturii -5 m.
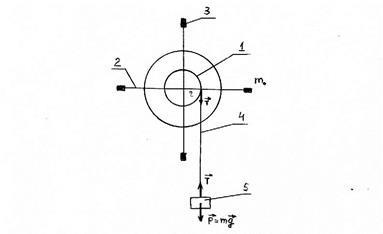
Datorită tensiunii firului sub acțiunea gravitației greutății suspendate, pendulul intră în mișcare, adică forța de tensionare a firului va fi forța pendulului rotativ, iar umărul acestei forțe va fi raza discului. Mișcarea sarcinii va fi accelerată uniform cu o accelerație a, care poate fi determinată din ecuația unei mișcări de translație accelerată uniform fără viteză inițială:
aici h este înălțimea căderii de sarcină,
a este accelerarea cu care se deplasează marfa,
t - timpul deplasării încărcăturii în jos.
Accelerația unghiulară este legată de relația liniară:
,
Tensiunea firului poate fi găsită din ecuația mișcării încărcăturii:
aici g este accelerația gravitației (g = 9,8 m / s 2).
Momentul forței de rotație este exprimat prin ecuația:
Aici r este raza discului pe care se înfășoară firul (vezi Figura 3.2.)
Înlocuindu-se valoarea e din ecuația (3.1) în ecuația (3.3), obținem:
ORDINEA DE PERFORMANȚĂ
- Măsurați diametrul discului cu ajutorul unui etrier.
- Ridicând încărcătura la o anumită înălțime, lăsați-o să coboare liber, rotind pendulul.
- Măsurați timpul în care se încadrează sarcina.
- Înregistrați rezultatele măsurătorilor în tabel.
Tabel pentru înregistrarea rezultatelor măsurătorilor
- Calculați accelerația pendulului prin ecuația (3.2).
- Calculați cuplul forței rotative din ecuația (3.4.)
- găsiți atitudinea.
- Calculați erorile.
- Construiește un grafic al funcției b = f (m)
- Folosind graficul funcției b = f (m), determinați momentul forțelor de frecare.
- Efectuați măsurători prin schimbarea distanței dintre mărfuri și axa de rotație. Comparați rezultatele.
- Formularea legii fundamentale a dinamicii mișcării de rotație.
- Care este momentul inerției unui punct material?
- Ce se numește momentul puterii?
- Care este momentul impulsului unui punct material?
- Care este unitatea de măsură a momentului forței în sistemul SI?
- Ce se numește umărul puterii?
- Care este unitatea de măsură a momentului forței în sistemul SI?
- Care este unitatea pentru măsurarea momentului unghiular al unui punct material în sistemul SI?
- Care este unitatea de măsurare a impulsului impuls al unei forțe în sistemul SI?
- Cum se determină momentul inerției unui corp solid?
LUCRAREA LABORATORULUI №4