Poziția de pornire poate fi descompusă în mai multe moduri. Total există
16! = 20 922 789 888 000 poziții inițiale.
Aceasta are în vedere locația celulei goale. De exemplu, aici este o poziție.
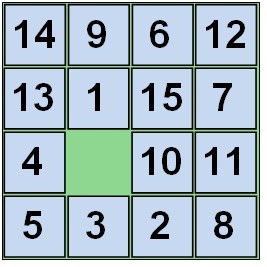
Dacă considerăm că o celulă goală este întotdeauna într-un singur loc (de exemplu, locul 1 este colțul din stânga sus - sau locul 16 este colțul din dreapta jos, o poziție goală), atunci ajungem
15! = 1 307 674 368 000 de articole.
De exemplu, aici este locația inițială
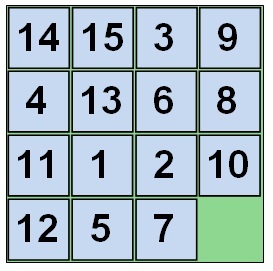
Aici este clar că o celulă goală este întotdeauna în colțul din dreapta jos.
Jumătate din toate mâinile sunt rezolvate. Cealaltă jumătate nu merge, întrucât vine vorba de această poziție:
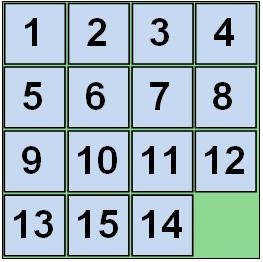
După cum vă amintiți, aceasta este sarcina lui Loyd.
Sper că înțelegeți că 50% dintre mâini nu vor putea fi colectate.
Orice poziție de pornire poate fi verificată pentru solvabilitate. Și nu încercați să-l colecteze și să vadă locația finală 15 și 14. Pentru a face acest lucru, va calcula doar „alinierea Paritate“, „tulburare parametru“ (acest termen așa cum doresc, și apeluri). În viața reală, este într-adevăr mai rapid să colectezi doar în jumătate de minut chips-uri și să vezi ce sa întâmplat, mai degrabă decât să numeri multiframele în mintea ta. Dar pentru exhaustivitate, vom studia teoria. Definiția parității este destul de complicată. Să vedem ce scrie Wikipedia:
Putem arăta că exact jumătate din toate posibile 20 922 789 888 000 poziții inițiale pyatnashek n evozmozhno duc la mintea colectate (= 16!): Lăsați cutia cu numărul I configurat (dacă numărul de la stânga la dreapta și de sus în jos) pătrate k cu numere mai mici i. Presupunem că n i = k. adică, dacă după numărul de articulații cu numărul i nu există numere mai mici decât i. apoi k = 0. Introducem de asemenea numărul e - numărul rândului din celula goală (numărând de la 1). În cazul în care suma
este ciudat, atunci soluția puzzle-ului nu există
Există o altă definiție care mi-a prins ochiul:
puzzle-ul are o soluție dacă parametrul așa numit tulburare (numărul de perechi de numere în care un număr mai mare precede cel mai mic cu adăugarea numărului rândului orizontal cu o celulă goală), un even
Deși este mai simplu, înțelesul este încă dificil de înțeles.
Să încercăm să explicăm într-un limbaj mai simplu cum să calculăm paritatea.
Pentru aceasta, trebuie să comparăm perechi de numere. Considerăm numărul acelor perechi în care un număr mai mare precede cele mai mici. Comparația se face cu privire la ordinea corectă. Numai la sfârșit nu uitați să adăugați numărul rândului cu o celulă goală - acest număr este de la 1 (linia de sus) la 4 (linia de jos). Din punct de vedere vizual, este posibil să se prezinte astfel:
Iată numerele elementului. În consecință, cu cât numărul este mai mic, cu atât mai devreme este poziția (sper, acest punct este clar).
De exemplu, luați acest aspect:
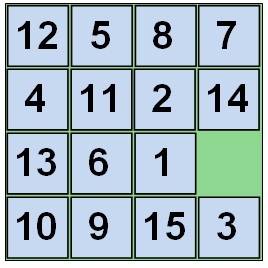
Aici, comparând perechile 5 și 2 vedem că 5. care este mai devreme, mai mult de două (2). atunci acesta este unul de care avem nevoie pentru un cuplu, îl vom calcula. Și 8 este mai mică de 11 și costă mai devreme, atunci nu considerăm o astfel de pereche.
Minoritatea teoriei: Există în total 15 chipsuri, care formează 105 de perechi (14 + 13 + 12 +. + 1). În practică, compararea celor 105 de perechi nu este atât de dificilă, ci este necesar să le contorizăm în mod clar. De exemplu, puteți face acest lucru (vedeți figura de mai sus):
Mai întâi luăm primul număr (avem 12). Contorizăm câte numere sunt mai puține după el. De exemplu, aceasta este unsprezece numere (de la 1 la 11 - aceste numere sunt mai mici și localizate mai târziu, adică după numărul 12 considerat de noi). Rezultatul a fost înregistrat.
Acum, luați al doilea număr (5). Considerăm cât de mult sunt mai mici după ea (nu "înainte", dar "după" - aceasta este pentru non-călători). După cele cinci, doar patru numere sunt mai tinere (de la 1 la 4). Rezultatul a fost adăugat la valoarea anterioară (11 + 4 = 15).
Acum luați al treilea număr (8) și luați în considerare și numărul de numere mai mici care stau după (cele șase, adică între 1 și 7, fără a număra 5, din moment ce cele cinci sunt mai devreme).
Și continuă.
Nu uitați chiar la sfârșit să adăugați un rând cu o cușcă goală. În exemplul nostru, acesta este al treilea rând.
Nu vom lua în considerare complet paritatea, aceste calcule sunt doar un exemplu de cum se procedează. Da, și este plictisitor să se ocupe de matematică în astfel de volume.
Numărătoarea totală va dura 5-10 minute. Dacă suma primită este egală, poziția va fi colectată. Dacă altfel (ciudat) - nu se va întâlni.
Structura indestructibilă (sfârșitul nesolvabil) Loida are paritatea "1" (numai 15 precede 14 și mai mult).
