Proprietățile adunării, scăderii, multiplicării și divizării sunt utile, deoarece vă permit să convertiți sume și produse în expresii convenabile pentru calcule. Vom învăța cum să simplificăm expresiile utilizând aceste proprietăți.
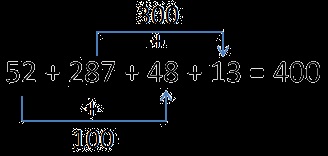
52 + 287 + 48 + 13 =
În această expresie, există numere care, atunci când se adaugă, se obțin cifre "rotunde". După ce am observat acest lucru, este ușor să efectuați verbale calculele. Folosim legea de deplasare a adunării.
De asemenea, pentru a simplifica calculul produselor, puteți utiliza legea de deplasare a multiplicării.
7 · 2 · 9 · 5 = (2,5) · (7,9) = 10,63 = 630
Combinarea și relocarea proprietăților sunt de asemenea utilizate atunci când simplificați expresiile literelor.
- 6 · a · 2 = 6 · 2 · a = 12a
- 2 · a · 4 · b = 2 · 4 · a · b = 8ab
- 5b + 8b = (5 + 8); b = 13b
- 14y - 12y = (14-12) y = 2y
Legea distributivă a multiplicării este adesea folosită pentru a simplifica calculele.
Aplicarea proprietății distributivă multiplicării peste adunare sau scădere a expresiei «(a + b) · c și (a - b) · c», obținem o expresie care nu conține paranteze.
În acest caz, ei spun că am deschis (a scăzut) parantezele. Pentru a aplica proprietățile, nu contează unde este scris multiplicatorul "c" - înainte de paranteze sau după.
Vom deschide parantezele în expresii.
- 2 (t + 8) = 2t + 16
- (3x - 5) 4 = 4 · 3x - 4 · 5 = 12x - 20
Dacă un număr nu este scris înaintea literei, atunci se presupune că litera este precedată de un multiplicator numeric de 1.
Punerea factorului comun în paranteze
Să schimbați partea dreaptă și cea stângă a ecuației:
În astfel de cazuri, se spune că un factor comun "c" este luat de la "ac + bc" pentru paranteze.
Exemple de a pune un factor comun în paranteze.
- 73 · 8 + 7 · 8 = (73 + 7) · 8 = 80 · 8 = 640
- 7x - x - 6 = (7 - 1) x - 6 = 6x - 6 = 6 (x - 1)