principal nbsp> nbsp tutorial Wiki nbsp> nbsp Math nbsp> clasa nbsp10 nbsp> nbsp Aplicații de continuitate: metoda interval și exemple
Se spune că funcția este continuă la punctul x0 dacă f (x) tinde să f (x0) pe măsură ce x tinde la x0. Mai mult decât atât, f (x) - A = f (x) - f (x0) = Δf. În cazul în care funcția f este continuă în fiecare punct al intervalului A, această funcție va fi continuă pe tot parcursul intervalului A. Și perioada a lui A, se numește în acest caz, un interval de continuitate a functiei f.
Program funcții continue studiate într-un curs de matematica pot fi trase „fără a lua creion pe hârtie“, deoarece reprezintă o linie continuă. Dacă pe un anumit interval (a; b) funcția f este continuă și nu dispare, atunci pe acest interval va păstra un semn constant.
Această proprietate este foarte ușor de înțeles. O funcție situată deasupra axei Ox are un semn plus, o funcție situată sub axa Ox are un semn minus. Dacă linia funcției nu intersectează axa Ox (pe axa Ox funcția este zero), atunci evident nu își schimbă semnul.
Metoda de intervale
Una dintre cele mai strălucite aplicații ale proprietăților continuității funcțiilor este metoda intervalului, care este folosită pentru a rezolva inegalitățile cu o variabilă. Să presupunem că o anumită funcție este continuă pe intervalul A și dispare la un număr finit de puncte aparținând acestui interval.
Folosind proprietatea de mai sus, aceste puncte vor rupe întregul interval A în intervale în care funcția va stoca semnul. Pentru a determina semnele tuturor intervalelor, este suficient să cunoașteți semnul unuia dintre aceste intervale.
Un exemplu de funcție care nu este continuă
Până acum am întâlnit doar funcții continue. Dar există funcții care nu sunt continue în fiecare punct în care sunt definite. De exemplu, funcția f (x) =, unde - este partea fracționată a numărului x. Graficul său este prezentat în figura următoare.
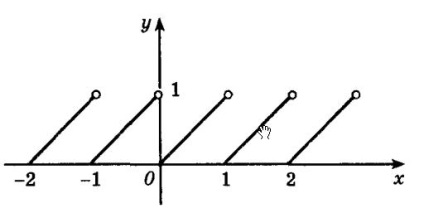
Este ușor de observat că proprietatea de bază a continuității unei funcții la un punct x0 egal cu orice număr întreg nu va fi satisfăcută. În același timp, funcția f (x) = este continuă în toate celelalte puncte pe care este definită, cu excepția punctelor unde x este un număr întreg. În grafic, aceste puncte sunt marcate cu cercuri perforate.
Funcțiile sunt continue, dar nu pot fi diferențiate la un anumit punct
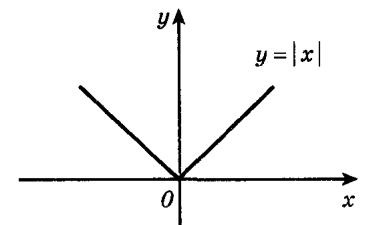
Există funcții care sunt continue în fiecare punct al domeniului lor de definiție. Dar nu vor avea derivate în anumite puncte. De exemplu, funcția y = | x | este continuă pe întreaga axă numerică, dar nu este diferențiată la punctul x = 0. Mai jos este un grafic al acestei funcții.