Metoda zonei Fresnel.
Calcule folosind formula
este, în general, o sarcină foarte dificilă. Cu toate acestea, așa cum se arată în fresnel cazuri de simetrie diferite, constatare care rezultă amplitudinea oscilației poate fi realizată printr-o însumare algebrică sau geometrice simple.
Să găsim într-un punct arbitrar M amplitudinea unei valuri sferice de lumină care se propagă într-un mediu omogen dintr-o sursă punctuală S.
Conform principiului Huygens-Fresnel, înlocuim acțiunea sursa acțiunii S surse imaginare situate la suprafață auxiliară F. care val suprafața frontală se extinde de la S (suprafața unei sfere cu centrul S). Fresnel a împărțit suprafața undelor A în zone inelare de o asemenea dimensiune încât distanțele de la marginile zonei la M diferă cu λ / 2,
O astfel de defalcare a frontului de undă în zone poate fi realizată prin realizarea cu centrul în punctul de divizare a frontierelor de valuri în zone care se pot executa prin desenarea cu centrul în punctul M a sferelor cu raze
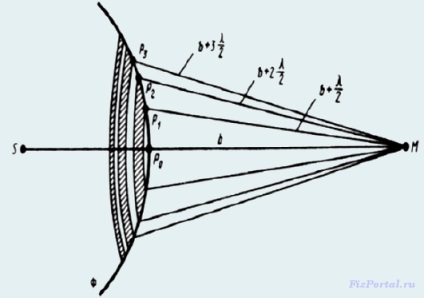
Deoarece oscilațiile din zonele învecinate trec la punctul M al distanței, cu o diferență de λ / 2. apoi ajung la punctul M în faza opusă, iar atunci când se impune aceste oscilații se vor slăbi unul pe celălalt. Prin urmare, amplitudinea vibrațiilor luminoase rezultate în punctul M:
unde A1. A2. ... Am sunt amplitudinile oscilațiilor excitate de i-a. Al 2-lea. ..., zonele m.
Pentru a estima amplitudinile de oscilație, găsim zonele din zonele Fresnel. Lăsați limita exterioară a zonei m alocă un segment sferic de înălțime hm pe suprafața undei (Fig.).
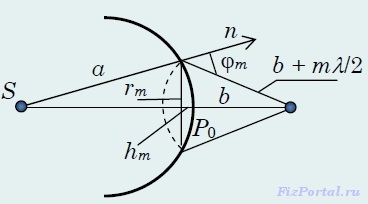
Indică raza acestui segment cu rm. constatăm că zona zonei Fresnel m:
aici σm-1 este aria segmentului sferic, care se distinge prin limita exterioară a zonei m. Din figura aceasta rezultă
După transformările elementare, luând în considerare faptul că λ <
Zona segmentului sferic și a zonei zonei m Fresnel:
unde δσm este aria zonei m Fresnel, care, după cum arată ultima expresie, nu depinde de m. Pentru m nu este prea mare, zonele din zonele Fresnel sunt aceleași.
Astfel, construcția zonelor Fresnel împarte suprafața undelor unui val sferic în benzi egale.
Să găsim razele zonelor Fresnel
de unde
Conform presupunerii lui Fresnel, efectul zonelor individuale în punctul M este mai mic, cu atât mai mare este unghiul φm între normal și suprafața zonei și direcția la M. acțiunea zonelor scade treptat de la central (aproximativ P0) la cele periferice. În plus, intensitatea radiației în direcția punctului M scade cu creșterea m și datorită creșterii distanței de la zonă la punctul M. Luând în considerare ambii acești factori, putem scrie:
Fazele oscilațiilor excitate de zonele învecinate diferă de π. Prin urmare, amplitudinea oscilației rezultate în punctul M este determinată de expresie
Ultima expresie este scrisă ca:
Datorită descrescătoare amplitudini ale zonelor monoton Fresnel, cu un număr de zonă crește, vibrațiile amplitudine sunt dintr-o zonă Fresnel m-lea este egal cu media aritmetică a amplitudinilor zonelor adiacente
atunci
Astfel, amplitudinea oscilațiilor rezultate într-un punct arbitrar M este determinată de acțiunea a numai jumătate din zona centrală Fresnel. În consecință, acțiunea întregii suprafețe de undă asupra punctului M este redusă la acțiunea regiunii sale mici, care este mai mică decât zona centrală.
Dacă un ecran opac este plasat pe traseul valului cu o deschidere care lasă doar prima zonă Fresnel deschisă, amplitudinea la punctul M este egală cu A1. iar intensitatea este de 4 ori mai mare decât în absența unei barieră între punctele S și M.
Propagarea luminii de la S la M are loc ca și cum fluxul de lumină se propagă într-un canal foarte îngust de-a lungul liniei drepte SM. și anume simplă. Astfel, principiul Huygens-Fresnel face posibilă explicarea propagării rectilinii a luminii într-un mediu omogen.
Validitatea divizării frontului de undă în zonele Fresnel a fost confirmată experimental. Dacă plasăm o plăcuță în calea undei luminoase care ar acoperi toate zonele parțiale sau parțiale Fresnel, atunci intensitatea luminii la punctul M crește brusc. Cu zonele închise chiar și Fresnel, amplitudinea punctului M va fi egală cu
În experiment, placa de zonă crește în mod intensiv intensitatea luminii în punctul M, acționând ca o lentilă de colectare.
Un efect și mai mare poate fi obținut fără suprapunerea zonelor Fresnel uniforme (sau impare) și prin schimbarea fazei oscilațiilor lor cu 180 °. O astfel de placă se numește placă de bandă de fază. În comparație cu placa de bandă de amplitudine, placa de fază oferă o creștere suplimentară a amplitudinii cu un factor de 2. și intensitatea luminii - de 4 ori.