Arabă Bulgară Chineză Croată Cehă Daneză Olandeză Engleză Estoniană Finlandeză Franceză Germană Greacă Hindi Indonezian Islandeză Italiană Japoneză Letonă Lituaniană malgașă Norvegiană Persană Poloneză Portugheză Română Rusă Sârbă Slovacă Slovenă Spaniolă Thai Turcă Vietnameză suedeză
Arabă Bulgară Chineză Croată Cehă Daneză Olandeză Engleză Estoniană Finlandeză Franceză Germană Greacă Hindi Indonezian Islandeză Italiană Japoneză Letonă Lituaniană malgașă Norvegiană Persană Poloneză Portugheză Română Rusă Sârbă Slovacă Slovenă Spaniolă Thai Turcă Vietnameză suedeză
definiție - Cerc
raportați o problemă
dicționar analogic

Cercul și centrul acestuia
Cercul este locusul geometric al punctelor planului. echidistant de la un punct dat, numit centru, de o distanță dată de zero. numit raza sa.
Alte definiții
Cercul de diametru AB este o cifră formată din punctele A, B și toate punctele planului din care segmentul AB este vizibil în unghi drept.
Un cerc este o cifră care constă din toate punctele dintr-un plan, pentru fiecare dintre acestea raportul distanțelor față de două puncte date este egal cu un număr dat diferit de unitate. (vezi Circumferința Apollonia)
De asemenea, o cifră constând din toate aceste puncte, pentru fiecare dintre acestea suma pătratelor de distanțe față de două puncte date este egală cu o valoare dată, mai mare decât jumătate din pătratul distanței dintre aceste puncte.
Definiții înrudite
- Raza nu este doar mărimea distanței, ci și lungimea. conectând centrul unui cerc cu unul din punctele sale.
- Un segment care unește două puncte dintr-un cerc se numește coarda acestuia. Coarda care trece prin centrul cercului se numește diametru.
- Un cerc este numit un cerc unic. dacă raza sa este egală cu una. Cercul unitar este unul dintre principalele obiecte ale trigonometriei.
- Orice două puncte care nu coincid într-un cerc îl împart în două părți. Fiecare dintre aceste părți este numită un arc de cerc. Arcul se numește semicerc. Dacă segmentul care leagă capetele este un diametru.
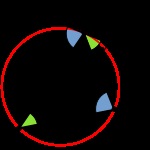
- Unghiul format dintr-un arc de cerc egal cu lungimea razei este considerat a fi un radian.
- Lungimea semicercului unității este notată cu.
- Poziția geometrică a punctelor pe un plan, distanța de la care până la un anumit punct nu este mai mare decât un anumit punct nenul, se numește cerc.
- O linie care are exact un punct comun cu un cerc se numește tangenta cercului, iar punctul lor comun este numit punctul de tangență al liniei și al cercului.
- O linie care trece prin două puncte diferite ale unui cerc se numește secant.
- Unghiul central este unghiul cu vârful din centrul cercului. Unghiul central este egal cu măsura gradului arcului pe care este susținut.
- Unghiul inscripționat este unghiul al cărui vârf se află pe cerc, iar laturile traversează acest cerc. Unghiul înscris este egal cu jumătate din măsura gradului arcului pe care se sprijină.
- Două cercuri având un centru comun sunt numite cercuri concentrice.
- Două cercuri care se intersectează în unghi drept. sunt numite ortogonale.
- Inegalitatea izoperimetrică. Din toate curbele închise la o anumită lungime, cercul limitează suprafața zonei maxime.
- O linie dreaptă poate să nu aibă puncte comune cu un cerc; au un punct comun (tangent) cu un cerc; să aibă cu ea două puncte comune (secant).
- Tangenta la un cerc este întotdeauna perpendiculară pe diametrul său, unul dintre ale cărui capete este punctul de tangență.
- Prin intermediul a trei puncte care nu se află pe o linie, puteți desena un cerc și mai mult decât unul.
- Punctul de tangență al celor două cercuri se află pe o linie care trece prin centrele lor.
- Lungimea arcului unui cerc de rază format din unghiul central măsurat în radiani. poate fi calculat din formula.
- Lungimea unui cerc cu o rază poate fi calculată din formula.
- Unghiul inscripționat este fie jumătate din unghiul central înclinat pe arcul său, fie completează jumătate din acest unghi la 180 °.
- Două unghiuri inscripționate, susținute de același arc, sunt egale.
- Unghiul inscripționat, susținut de un arc de jumătate din circumferință, este de 90 °.
- Unghiul dintre două secante trase dintr-un punct situat în afara cercului este egal cu jumătatea diferenței dintre măsurătorile arcilor situate între secante.
- Unghiul dintre acordurile intersectate este egal cu jumătate de sumă a măsurilor arcului care se află în unghi și arcul opus acestuia.
- Unghiul dintre tangent și coardă este egal cu jumătate din măsura gradului arcului contractat de coardă.
- Segmentele tangentelor la cercul tras dintr-un punct sunt egale și egale cu unghiurile de la linia care trece prin acest punct și centrul cercului.
- Atunci când se intersectează două coarde, produsul segmentelor în care unul este împărțit prin punctul de intersecție este egal cu produsul segmentelor celuilalt.
- Produsul lungimilor distanțele de la punctul selectat la două puncte de intersecție a unui secantă și circumferința care trece prin punctul selectat, nu depinde de secante și egale valorile absolute ale puterii unui punct.
- Pătratul lungimii segmentului tangent este egal cu produsul lungimilor secțiunilor secantului și este egal cu valoarea absolută a gradului punctului față de cerc.
- Un cerc este o curbă simplă plană a ordinii a doua.
- Un cerc este o secțiune conică și un caz special de elipsă.
Formulele de bază
Domeniul sectorului. delimitată de un unghi α. măsurată în grade, raza R:
Zona segmentului. delimitată de un arc de cerc cu un unghi α. coardă:

Un cerc cu raza r = 1, centrul (a. B) = (1,2, -0,5)
Ecuația generală a unui cerc este scrisă ca:
Un punct este centrul unui cerc, raza lui.
Ecuația unui cerc de rază cu centrul la origine:
Ecuația unui cerc care trece prin trei puncte (folosind determinantul) și
Un cerc poate fi de asemenea descris folosind o ecuație parametrică:
Într-un sistem de coordonate cartezian, cercul nu este un grafic de funcții. dar poate fi descris ca combinând graficele următoarelor două funcții:
Dacă centrul cercului coincide cu originea, funcțiile iau forma:
Raza cercului cu centrul în punctul:
Dacă coordonatele polare ale centrului cercului, atunci cercul care trece prin originea coordonatelor este descris de ecuația:
Dacă centrul este originea coordonatelor, atunci ecuația va avea forma:
Pe un plan complex, cercul este dat de formula:
sau în forma parametrică
Tangenți și normali
Ecuația tangentei la cerc la un punct este dată de
Ecuația normală din același punct poate fi scrisă ca
Cercuri concentrice și ortogonale
Două cercuri definite de ecuații:
sunt concentrice (adică, au un centru comun) dacă și numai dacă u
Două cercuri sunt ortogonale (adică se intersectează într-un unghi drept) dacă și numai dacă există condiție