Capitolul 4. Modele matematice de optimizare
1. O funcție f (x) se spune a fi convexă dacă se află în întregime cel mult un segment care unește două puncte arbitrare din ea. Se spune că o funcție este strict convexă dacă se află în întregime sub un segment care unește două puncte arbitrare, dar nu coincide.
2. Dacă funcția este puternic convexă, atunci este simultan strict convexă și convexă. Dacă funcția este strict convexă, atunci este simultan convexă.
3. Convexitatea unei funcții poate fi determinată din matricea hessiană:
· Dacă H (x) φ 0 "x Î R n. atunci funcția este convexă;
· Dacă H (x)> 0-x Î R n. atunci funcția este strict convexă;
· Dacă H (x) ≥ lE "x Î R n. unde E este matricea identității, atunci funcția este puternic convexă.
Observăm proprietatea importantă a unei funcții convexe. Dacă funcția f este convexă pe setul X, atunci pentru orice puncte x1. x2. xm ÎX și numerele arbitrare nonnegative l1 + l2 +. lm = 1 se află următoarea inegalitate: Ian Sen
Pentru m = 2 această inegalitate coincide cu inegalitatea (3.1) din definiția unei funcții convexe.
Prin ea însăși, afirmația problemei de optimizare este simplă și naturală: Având în vedere un set X și o funcție £ (x) definită pe x, este necesar să se găsească punctele minime sau maxime ale funcției £ pe x. Sarcina minimă este scrisă ca:
În acest caz, se va numi funcția obiectivă. x este un set admisibil, orice element x ÎX este un punct admisibil al problemei (4.1). Dacă x coincide cu întregul spațiu, problema 4.1 este numită problema minimizării necondiționate (fără restricții), altfel - problema minimizării condiționate (cu constrângeri).
a) liniară (I, II) și neliniară (III, IV) (figura 4.1);
b) deterministic (A.B.) și stasistatic (grupuri de curbe Cj) (Fig.4.2).
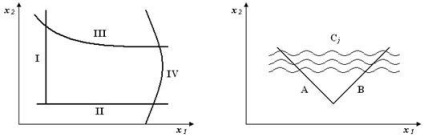
Fig. 4.3 O curbă arbitrară cu două minime locale.
Astfel, minimul global este cel mai mic dintre toate minimele locale. În Fig. 4.3 prezintă punctele minimelor locale și globale pentru o curbă arbitrară | (x).
Problema de optimizare, în care criteriul de optimitate | (x) are un minim local unic în domeniul X, se numește o problemă de optimizare un-extremă (unimodală). Cele mai simple dintre funcțiile unimodale sunt funcțiile convexe (figura 4.4.a).
Figura 4.4 prezintă exemple de funcții unimodale unimodale.
Problema de optimizare, în care criteriul de optimitate f (x) are mai multe minime locale, se numește problema optimizării multiextremale.
Metodele obișnuite pentru rezolvarea multor probleme extreme asigură găsirea unui singur punct singular în care derivatul parțial. Un astfel de punct, în funcție de circumstanțele aleatoare (alegerea aproximării inițiale) poate fi oricare dintre minima locală sau punctul de inflexiune. În legătură cu aceasta, este esențial să se cerceteze condițiile în care soluția asigură un minim global.
În cazul în care inegalitatea (4.2) sau (4.3) are ca strictă atunci când h¹h *, noi spunem că x * este un punct de minim strict (soluție riguroasă) pe un sens global sau local. Este clar că soluția globală este și locală; conversația nu este adevărată.
Pentru a reflecta faptul că punctul x *ÎX este un punct al minimului global al funcției £ pe X, vom folosi notația:
sau o înregistrare echivalentă
Se spune că punctul x * realizează o valoare, adică, valoarea minimă a funcției £ pe X. Setul tuturor punctelor din minimul global | pe X este notat cu
Astfel, Argmin | (x) este pur și simplu un punct arbitrar din set.
Dacă este necesar, problema de minimizare poate fi înlocuită de problema de maximizare sau invers. Acest lucru se datorează faptului că minimum de | egal cu funcția maximă - | luată cu semn opus, și a obținut ambele extreme la aceleași valori ale variabilelor (Figura 4.5). În punctul x * min | (x *) = -max (- | (x *)).
Fig.4.5 Pentru formularea problemei de optimizare.
Astfel, în cazul în care, de exemplu, problema minimizării funcției pentru orice restricții pe care doriți să le înlocuiți problema maximizare, este suficient pentru a pune împreună ca funcția țintă - pentru a găsi maximum de această funcție și înlocuiți-l cu semnul opus. Valoarea obținută va fi optimă a problemei inițiale. În analogia cu (4.1), scriem problema maximizării funcției £ pe setul X în forma:
Soluțiile de probleme (4.1) și (4.4), adică Punctele minime și maxime ale funcției £ pe X sunt de asemenea numite puncte extremum. iar problemele (4.1) și (4.4) sunt probleme extreme.