Un exemplu de rezolvare a unei probleme de transport folosind MS Excel
Problema transportului este sarcina clasică de a investiga operațiunile. Multe sarcini de alocare a resurselor sunt reduse la această sarcină.
Ferma dispune de cinci depozite de îngrășăminte minerale și patru puncte unde trebuie livrate. Nevoia de fiecare element în îngrășămintele minerale variază, iar stocurile din fiecare depozit sunt limitate. Este necesar să se determine de la care depozit până la ce punct să se livreze, câte îngrășăminte minerale să minimizeze cifra de afaceri de transport.
Sunt disponibile următoarele date inițiale.
Disponibilitatea îngrășămintelor minerale în depozite.
La intersecția coloanei punctului de livrare specific cu linia de depozit se găsesc informații despre distanțele dintre acest punct de livrare și depozit. De exemplu, distanța dintre punctul 3 și depozitul 3 este de 10 kilometri.
Pentru a rezolva problema, pregătim mesele necesare. (Figura 1)
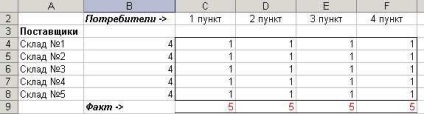
Fig.1 Celule modificabile.
Valorile celulelor din coloana B din rândul patru până la al optulea sunt determinate prin însumarea datelor celulelor rândurilor corespunzătoare din coloana C în coloana F.
De exemplu, valoarea celulei B4 = SUM (C4: F4)
Valorile celulelor din rândul 9 pe coloanele de la C la F se determină prin însumarea datelor de celule ale coloanelor corespunzătoare de la 4 la 8 linii.
De exemplu, valoarea celulei C9 = SUM (C4: C8)
Fiecare valoare în celula de la intersecția unei coloane dintr-un anumit element de stocare și livrare linie înseamnă numărul de tone livrate cu acest depozit la punctul de consum. Linia de jos (linia 9) a rezumat cantitatea totală de îngrășăminte minerale furnizate la un anumit punct de livrare, iar a doua coloană (coloana B) se însumează cu valoarea îngrășămintelor depozit de beton livrate.
Acum, folosind datele inițiale, vom introduce pe aceeași foaie volumele necesare de livrări și distanțele dintre depozite și punctele de livrare.
Fig.2 Informații de bază.
În linia 16 în coloanele C-F, definim cifra de afaceri pentru fiecare punct de livrare. De exemplu, pentru 1 punct (celula C16), aceasta se calculează folosind formula
С16 = С4 * С1 1 + С5 * С1 2 + С6 * С1 3 + С7 * С14 + С8 * С15
sau puteți utiliza funcția SUMPRODUCT
Celula C4 conține cantitatea de îngrășăminte minerale transportate din punctul de livrare nr. 1 la 1, iar celula C11 este distanța de la punctul de depozit nr. 1 la 1. În consecință, primul termen din formula reprezintă cifra de afaceri totală a mărfurilor pe această rută. Întreaga formulă calculează cifra de afaceri totală a transportului de îngrășăminte minerale în 1 punct de livrare.
În celula B16, utilizând formula = SUM (C16: F16), se calculează volumul total al traficului de încărcături al îngrășămintelor minerale.
Astfel, informațiile din foaia de lucru au următoarea formă (Figura 3)

Fig. 3. Foaia de lucru pregătită pentru rezolvarea sarcinii de transport
Pentru a rezolva problema de transport, folosim procedura Find Solution, care este localizată în meniul Tools (Instrumente).
După selectarea acestei comenzi, apare o casetă de dialog (Figura 4).
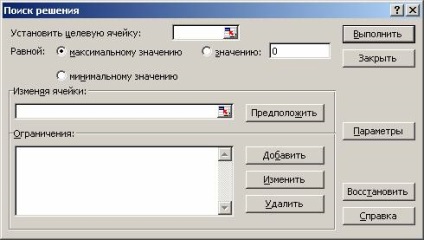
Fig. 4. Caseta de dialog Find Solution
Pentru ca, criteriul nostru de optimizare este ales pentru a minimiza cifra de afaceri în domeniu pentru a stabili o celulă țintă, introduceți referința celulei care conține formula de calcul a volumului cifrei de afaceri bschego îngrășăminte. In acest caz, celula $ B $ 1 6. Pentru a minimiza valoarea celulei finale prin schimbarea valorilor celulelor de influență (care afectează, în acest caz, și schimbarea sunt celule care sunt folosite pentru a stoca valori necesare necunoscute), comutatorul este setat la valoarea minimă;
În câmpul Modificați celule, introduceți referințele la celulele care trebuie modificate, separate prin virgule; sau dacă celulele sunt în apropiere, indicând prima și ultima celulă, separându-le cu un colon ($ C $ 4: $ F $ 8). Aceasta înseamnă că, pentru a atinge o cifră de afaceri minimă de transport, valorile din celulele C4 până la F8 se vor schimba. adică cantitatea de mărfuri transportată pe o anumită rută se va schimba.
Dacă începem acum procesul de selectare a parametrilor, vom găsi o variantă în care toate variabilele sunt zero. Și acest lucru este corect - dacă nu transportați nimic, atunci aceasta este cea mai ieftină opțiune. Dar trebuie să transportăm îngrășăminte minerale, așa că trebuie să impunem anumite limitări pentru a găsi o soluție.
În grupul Limite de câmpuri, faceți clic pe Adăugați. Se va afișa caseta de dialog Adăugare constrângere (Figura 5)
Fig. 5. Caseta de dialog Add Constraint
Trebuie să introduceți partea stângă a constrângerii în marginea din stânga, să selectați semnul condiției care este suprapusă peste valoare și să introduceți partea dreaptă a constrângerii. Ca și în alte cazuri, nu puteți introduce linkuri către celule, ci selectați aceste celule cu mouse-ul. După ce introduceți o restricție, faceți clic pe butonul Adăugați și introduceți următoarele. Când terminați introducerea tuturor restricțiilor, faceți clic pe OK. În dialog sunt introduse linii de restricții (Figura 6)
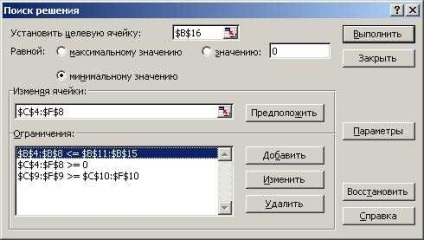
Fig. 6. Caseta de dialog Find Solution cu câmpuri completate
Pentru a modifica și elimina restricțiile din lista Limite din caseta de dialog Căutarea soluției, specificați restricția pe care doriți să o modificați sau să o ștergeți. Selectați Modificați și efectuați modificări sau faceți clic pe Eliminare.
Să analizăm în detaliu condițiile care ar trebui impuse valorilor din unele celule pentru rezolvarea corectă a problemei.
Prima condiție $ B $ 4: $ B $ 8 <=$B$11:$B$12. Оно означает, что значение в ячейке В4 должно быть меньше или равно значению в В11. в В5 меньше или равно, чем в В12. и так далее до В8 и В15.
În celulele B4-B8 de pe foaie sunt volumele de livrări din depozite specifice. În celulele B11 până la B15 - stocurile din aceleași depozite. Deoarece este imposibil să se retragă mai mult din depozit decât este, prima valoare nu ar trebui să fie mai mare decât a doua.
A doua condiție este $ C $ 4: $ F $ 8> = 0. Aceasta înseamnă că volumul traficului nu poate fi negativ, adică dacă în depozit nu există suficientă îngrășăminte minerale, ele nu sunt luate de la punctul de livrare la care au fost importate mai devreme aceste îngrășăminte minerale. Traficul de marfă are o singură direcție - de la depozite până la punctele de livrare a îngrășămintelor.
În cele din urmă, a treia și ultima condiție este $ C $ 9: $ F $ 9 = $ C $ 10: $ F $ 10. Aceasta înseamnă că valorile din celulele celei de a noua linii trebuie să fie mai mari sau egale cu valorile din celulele liniei a zecea. adică cererile de puncte de livrare pentru îngrășămintele minerale trebuie să fie implementate pe deplin. Suprafața volumului de livrări este admisibilă, iar subaplicarea nu este.
Condițiile introduse ar trebui să ne permită găsirea celei mai optime soluții a problemei. Faceți clic pe butonul Executare pentru a selecta soluția.
După găsirea soluției, apare dialogul Rezultatele soluției de soluție (Figura 7)
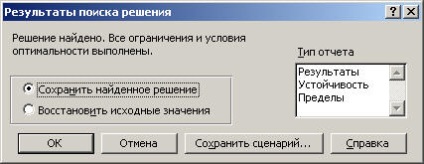
Fig. 7. Caseta de dialog Search Solution
Dacă faceți clic pe butonul OK, soluția va apărea în foaia de lucru (Figura 7).
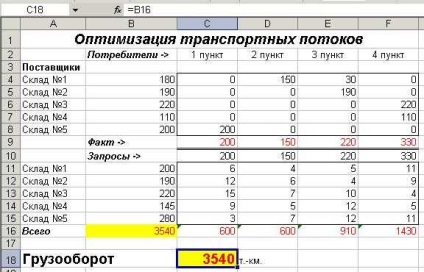
Fig. 7. Problema de transport rezolvată
Rotația minimă a transportului de mărfuri cu respectarea tuturor condițiilor este egală cu 3540 t.km.