
Uneori, oamenii care nu sunt legați de matematică sunt întrebați: care este cel mai mare număr? Pe de o parte, răspunsul este evident - infinit. Nerezurile specifică chiar "plus infinit" sau "+ ∞" în înregistrarea matematicienilor. Acesta este doar cel mai prudent răspuns nu va convinge, mai ales că nu este un număr natural, ci o abstractizare matematică. Dar dacă ați înțeles bine problema, ei pot deschide o problemă foarte interesantă.
Într-adevăr, limita de mărime în acest caz nu există, dar există o limită pentru imaginația umană. Pentru fiecare număr există un nume: zece, o sută, un miliard, un sextilliard și așa mai departe. Dar unde se termină fantezia oamenilor?
Nu trebuie confundat cu marca comercială a Google, deși are o origine comună. Acest număr este scris ca 10100, adică unul și în spatele lui este o valoare zero. Este dificil de prezentat, dar a fost folosit în mod activ în matematică.
Este amuzant ce a venit copilul său - nepotul matematicianului Edward Kazner -. În 1938, unchiul meu ia distrat pe rudele sale mai tinere cu argumente despre un număr foarte mare. Pentru indignarea copilului sa dovedit că un astfel de număr remarcabil nu are nume și el a dat versiunea sa. Mai târziu, unchiul la pus într-una din cărțile sale, iar termenul sa răzgândit.
Teoretic, googolul este un număr natural, deoarece poate fi folosit pentru numărare. Dar este puțin probabil ca cineva să aibă răbdarea să numere până la capăt. Prin urmare, doar teoretic.

În ceea ce privește numele Google, atunci eroarea obișnuită sa strecurat. Primul investitor si unul dintre co-fondatorii atunci când scrieți un cec, în grabă, și am ratat litera „O“, ci pentru a încasa compania sa a trebuit să-l înregistreze în astfel de grafii.
googolplex
Acest număr este un derivat al googolului, însă semnificativ mai mare decât acesta. Prefixul "plex" înseamnă ridicarea a zeci la puterea egală cu numărul de bază, astfel încât guloplexul este de 10 la puterea de 10 la puterea de 100 sau 101000.
Numărul rezultat - depășește numărul de particule din universul previzibil, care este estimat undeva la gradul 1080. Dar acest lucru nu a împiedicat oamenii de știință să crească numărul adăugând un prefix "plex": gugolplexplex, gugollexlexlex și așa mai departe. Iar pentru un matematicieni deosebit de pervers a inventat o variantă de creștere, fără prefix repetiție fără sfârșit „plex“ - în fața ei a pus doar numărul de tetra grecesc (patru), Penta (cinci), și așa mai departe, până la puntea (zece). Ultima variantă pare a fi un Gugol de Duplex și înseamnă o repetare cumulativă de zece ori a procedurii de ridicare a numărului 10 până la gradul de fundamentare a acesteia. Principalul lucru nu este să ne imaginăm rezultatul. Pentru a realiza totul nu funcționează, ci pentru a obține o traumă a psihicului - cu ușurință.
Numărul 48 din Mersen

Caractere principale: Cooper, computerul său și un nou număr
Mai recent, cu aproximativ un an în urmă, a fost posibil să se deschidă următorul număr, 48 de Mersen. În prezent este cel mai mare număr din lume. Reamintim că numerele prime sunt cele care se împart fără un rest doar de unul și de ele însele. Cele mai simple exemple sunt 3, 5, 7, 11, 13, 17 și așa mai departe. Problema este că mai departe în junglă, cu atât mai puține ori apar astfel de numere. Dar cu atât mai valoros este descoperirea fiecăruia dintre următoarele. De exemplu, un nou număr prime constă în 17 425 170 de caractere, dacă îl reprezentați sub forma unui sistem zecimal numeric obișnuit. În precedent au existat aproximativ 12 milioane de semne.
A fost descoperită de matematicianul american Curtis Cooper, care pentru a treia oară a bucurat comunitatea matematică cu un astfel de record. Doar pentru a verifica rezultatul și pentru a dovedi că acest număr este foarte simplu, au fost necesare 39 de zile de lucru ale calculatorului său personal.
Numărul Graham
Acesta este modul în care se înregistrează numărul lui Graham în notația de participare a lui Knuth. Este dificil să spunem cum să descifrăm acest lucru, fără a avea o educație superioară completă în matematica teoretică. De asemenea, este imposibil să o scrieți în forma zecimală obișnuită: universul observabil pur și simplu nu îl poate conține. Pentru a construi un grad într-o anumită măsură, ca și în cazul gugololelor, nu este de asemenea o opțiune.
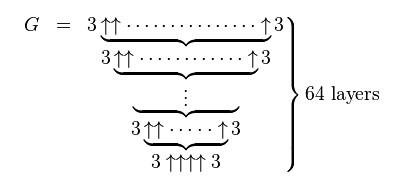
O formulă bună, doar de neînțeles
De ce avem nevoie de acest număr inutil la prima vedere? În primul rând, a fost plasat în Cartea Recordurilor Guinness pentru oameni curioși, iar acest lucru este deja destul de mult. În al doilea rând, a fost folosit pentru a rezolva problema care face parte din problema Ramsey, care este, de asemenea, neclare, dar pare a fi serioasă. În al treilea rând, acest număr este recunoscut ca cel mai mare, folosit vreodată în matematică, și nu în dovezi comice sau jocuri intelectuale, ci pentru a rezolva o problemă matematică foarte specifică.
Atenție vă rog! Următoarele informații sunt periculoase pentru sănătatea dvs. mintală! Citiți-o, vă asumați responsabilitatea pentru toate consecințele!
Pentru cei care doresc să-și testeze mintea și să mediteze asupra numărului Graham, putem încerca să-i explicăm (dar numai să încercăm).
Imaginați-vă 33. Este destul de ușor - se dovedește 3 * 3 * 3 = 27. Și dacă acum construiești un triplu în acest număr? Va fi de 3 3 până la 3 grade, sau 3 27. În zecimale acest lucru este 7 625 597 484 987. O mulțime, dar până acum se poate realiza.
În nota săgeții lui Knuth, acest număr poate fi afișat ceva mai simplu - 3 ↑↑ 3. Dar dacă adăugați o singură săgeată, se va dovedi a fi mai complicată: 3 ↑↑↑ 3, ceea ce înseamnă 3 ↑↑ 3 la puterea lui 3 ↑↑ 3 sau într-o înregistrare a puterii. Dacă extindeți la un punct zecimal, veți obține 7 625 597 484 987 7 625 597 484 987. Încă mai urmează să urmați acest gând?
Următoarea etapă: 3 ↑↑↑↑ 3 = 3 ↑↑↑↑ 3 3 ↑↑↑↑ 3. Aceasta înseamnă că trebuie să calculați acest număr sălbatic din acțiunea anterioară și să-l ridicați în aceeași măsură.
Și 3 ↑↑↑↑ 3 este doar primul dintre cei 64 de membri ai numărului Graham. Pentru a obține a doua, trebuie să calculați rezultatul acestei formule furioase și să înlocuiți numărul corespunzător de săgeți din schema 3 (↑ ... ↑) 3. Și așa mai departe, de 63 ori.
Interesant este că cineva, alături de el și o duzină de supermathematicieni, va ajunge cel puțin la mijlocul secvenței și nu va da jos cu asta?
Înțelegi ceva? Nu o facem. Dar ce fiori!