Una dintre secțiunile de matematică cu care studenții se confruntă cu cele mai mari dificultăți este trigonometria. Nu este surprinzător: să stăpânească în mod liber acest domeniu al cunoașterii, este nevoie de o gândire spațială, capacitatea de a găsi sinus, cosinus, tangenta, cotangentă de formule pentru a simplifica exprimarea, pentru a putea fi utilizate la calcularea valorii Pi. În plus, trebuie să puteți aplica trigonometria în dovada teoriei și aceasta necesită fie memorie matematică avansată, fie capacitatea de a deriva lanțuri logice complexe.
Originea trigonometriei
Familiarizarea cu această știință ar trebui să înceapă cu definirea sinusului, cosinusului și tangentei unghiului, dar mai întâi trebuie să înțelegem ce înseamnă trigonometria în general.

Etapa inițială
Inițial, oamenii au vorbit despre relația dintre unghiuri și laturi exclusiv pe exemplul de triunghiuri dreptunghiulare. Apoi s-au deschis formule speciale care au permis extinderea limitelor de utilizare în viața de zi cu zi a acestei secțiuni de matematică.
Studiul trigonometrie azi la școală începe cu un triunghiuri unghi drept, iar apoi utiliza cunoștințele dobândite de studenți în fizică și rezolvarea ecuațiilor trigonometrice abstracte, lucru care începe în liceu.
Trigonometria sferică
Mai târziu, când știința a ajuns la următorul nivel de dezvoltare, s-au folosit formule cu un sinus, cosinus, tangent, cotangent în geometrie sferică, unde funcționează și alte reguli, iar suma unghiurilor în triunghi este întotdeauna mai mare de 180 de grade. Această secțiune nu este studiată la școală, dar trebuie să știm despre existența ei cel puțin pentru că suprafața pământului și suprafața oricărei alte planete sunt convexe, ceea ce înseamnă că orice marcare a suprafeței va fi "în formă de arc" în spațiul tridimensional.
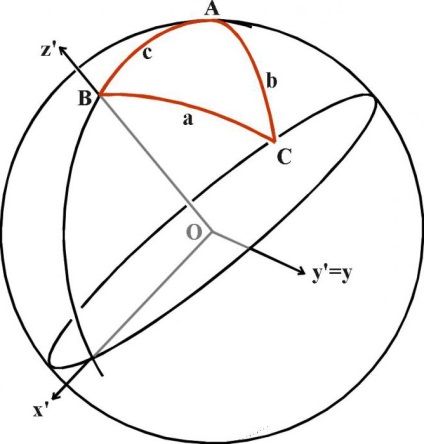
Dreptunghiular triunghi
Câteva metode de învățare despre aplicarea trigonometrie, vom reveni la trigonometria de bază pentru a înțelege mai bine ceea ce un sinus, cosinus, tangenta, unele calcule le pot folosi pentru a efectua și ce fel de formula în care se utilizează.
În primul rând, este necesar să înțelegem conceptele legate de un triunghi în unghi drept. În primul rând, hypotenuse este partea care se află opus unghiului de 90 de grade. Este cea mai lungă. Ne amintim că prin teorema lui Pitagora, valoarea sa numerică este egală cu rădăcina sumelor dintre pătratele celorlalte două părți.
De exemplu, dacă cele două laturi sunt de 3 și respectiv 4 centimetri, lungimea hipotenentei va fi de 5 centimetri. Apropo, vechii egipteni știau despre asta acum patru ani și jumătate de mie de ani.
Cele două laturi rămase, care formează un unghi drept, se numesc catetete. În plus, trebuie să ne amintim că suma unghiurilor din triunghi într-un sistem de coordonate dreptunghiular este de 180 de grade.
definiție
În cele din urmă, înțelegând cu fermitate baza geometrică, se poate ajunge la definiția sinusului, cosinusului și tangentei unghiului.
Un sinus al unui unghi este raportul piciorului opus (adică, partea opusă unghiului dorit) față de hypotenuse. Cosinusul unghiului este raportul piciorului adiacent la hypotenuse.

În cele din urmă, tangenta unghiului este raportul dintre partea opusă și partea adiacentă. Același rezultat va duce la împărțirea sinusului cu cosinusul. Uită-te: conform formulei, împărțim lungimea laterală de către hipotensiune, apoi împărțim după lungimea celei de-a doua părți și înmulțim cu hipotensiunea. Astfel, obținem aceeași relație ca și în definiția tangentei.
Cotangent, respectiv, este raportul dintre partea adiacentă colțului și partea opusă. Acelasi rezultat se obtine prin impartirea unitatii prin tangenta.
Deci, am luat în considerare definițiile a ceea ce este un sinus, cosinus, tangent și cotangent și putem face față formulelor.
Cele mai simple formule
În trigonometrie, nu puteți face fără formule - cum să găsiți un sinus, cosinus, tangent, cotangent fără ele? Dar aceasta este ceea ce este necesar pentru rezolvarea problemelor.
Prima formulă pe care trebuie să o cunoașteți atunci când începeți să învățați trigonometria este că suma pătratelor sinusului și cosinusului unghiului este una. Această formulă este o consecință directă a teoremei pitagoreene, dar economisește timp dacă doriți să cunoașteți magnitudinea unghiului, nu partea.
Mulți studenți nu se pot aminti a doua formulă este, de asemenea, foarte popular în rezolvarea problemelor școlare: cantitatea de unități și tangenta pătrat este egală cu una împărțită la pătratul cosinusul unghiului. Priviți mai atent: aceasta este aceeași declarație ca și în prima formulă, numai ambele părți ale identității au fost împărțite într-un pătrat al cosinusului. Se pare că o simplă operație matematică face ca formula trigonometrică să fie complet nerecunoscută. Amintiți-vă, știind ce sinus, cosinus, tangenta și cotangentă, regulile de transformare, și câteva formule de bază, puteți aduce întotdeauna ei înșiși nevoie de formule mai complicate pe o bucată de hârtie.
Formule cu două unghiuri și adăugarea de argumente
Două alte formule pe care doriți să le învățați sunt legate de valorile sinusoidale și cosinuse pentru suma și diferența unghiurilor. Acestea sunt prezentate în figura de mai jos. Rețineți că, în primul caz, sinusul și cosinusul se înmulțesc de două ori, iar în cel de-al doilea caz se adaugă un produs pereche de sinus și cosinus.
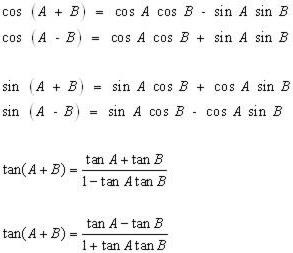
În cele din urmă, rețineți că formulele cu unghi dublu pot fi transformate astfel încât să scadă gradul de sinus, cosinus, tangent alfa.
Două teoreme de bază în trigonometria de bază sunt teorema sine și teorema cosinus. Cu ajutorul acestor teoreme, puteți înțelege cu ușurință cum să găsiți sinus, cosinus și tangent și, prin urmare, zona figurinei, dimensiunea fiecărei părți și așa mai departe.
Teorema sinusală afirmă că, ca urmare a împărțirii lungimii fiecărei laturi a triunghiului cu valoarea unghiului opus, obținem același număr. Mai mult decât atât, acest număr va fi egal cu două raze ale cercului circumscris, adică un cerc care conține toate punctele triunghiului dat.

Erori prin neatenție
Chiar dacă știm ce este sinus, cosinus și tangent, este ușor să faci o greșeală din cauza distragerii atenției sau a erorii în cele mai simple calcule. Pentru a evita astfel de greșeli, ne vom familiariza cu cele mai populare.
În al treilea rând, nu confundați valorile pentru unghiurile de 30 și 60 de grade pentru sines, cosines, tangente, cotangente. Amintiți-vă aceste valori, deoarece sinusul este de 30 de grade egal cu cosinusul de 60 și invers. Ele sunt ușor de confundat, astfel încât veți obține în mod inevitabil o eroare.
cerere
Mulți studenți nu se grăbesc să înceapă să studieze trigonometria, deoarece nu înțeleg sensul său aplicat. Ce este un sinus, cosinus, tangent pentru un inginer sau un astronom? Acestea sunt concepte prin care poți calcula distanța până la stele îndepărtate, prezice căderea unui meteorit, trimite o probă unei alte planete. Fără ele nu puteți construi o clădire, nu puteți proiecta o mașină, nu calculați sarcina pe suprafață sau traiectoria mișcării obiectului. Și acestea sunt doar exemplele cele mai evidente! La urma urmei, trigonometria într-o formă sau alta este folosită peste tot, de la muzică la medicină.
În concluzie
Deci, știi ce este sinus, cosinus, tangent. Le puteți folosi în calcule și rezolvați cu succes problemele școlare.
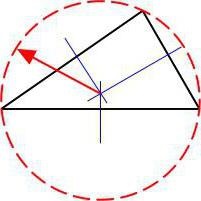
Cum să găsiți sinusul, cosinusul, tangentul de la lungimile cunoscute ale picioarelor sau hypotenuse, știți acum. Deoarece acești termeni nu se referă pur și simplu raportul, iar raportul - este o fracție, scopul principal al problemei trigonometric devine găsirea unei ecuații normale sau rădăcinile ecuații. Și aici veți fi ajutați de matematica școlară obișnuită.

