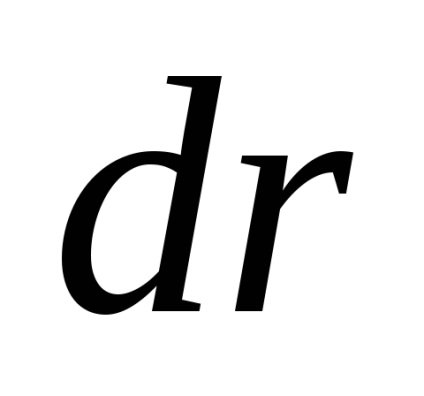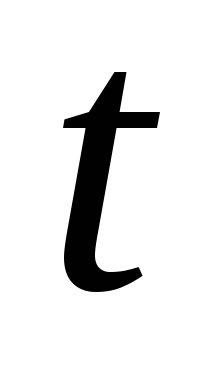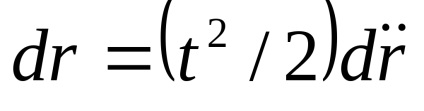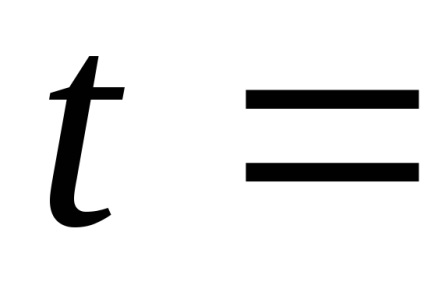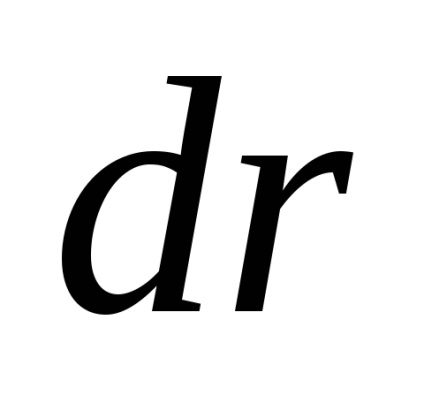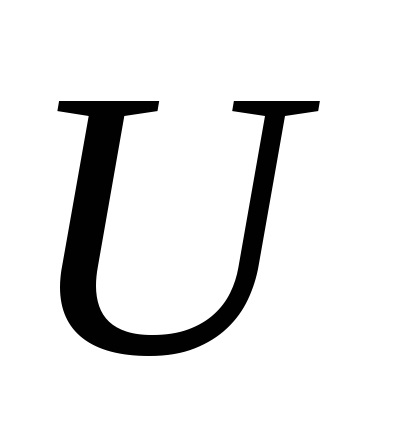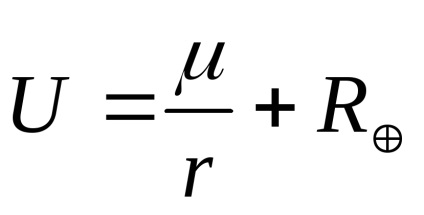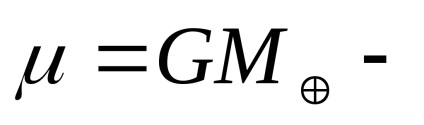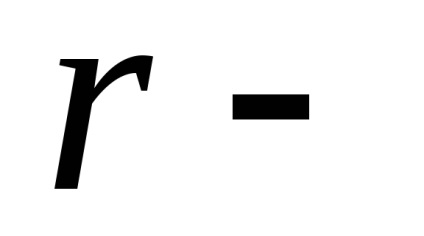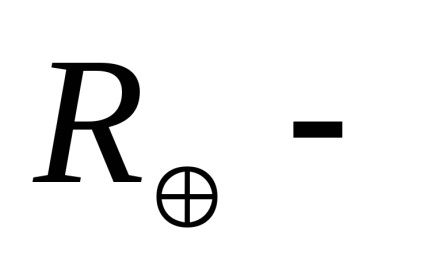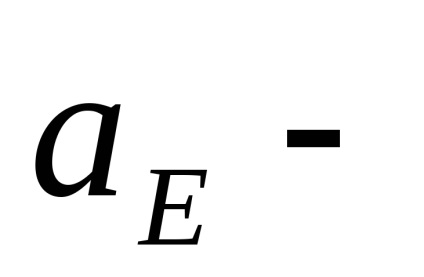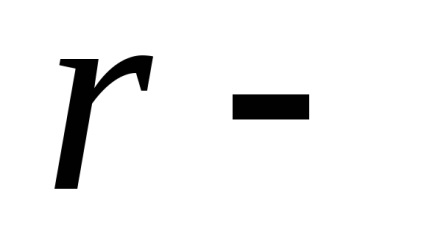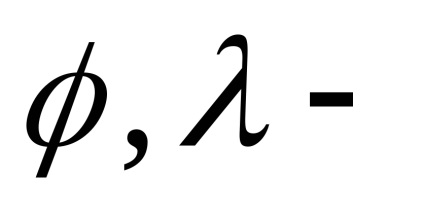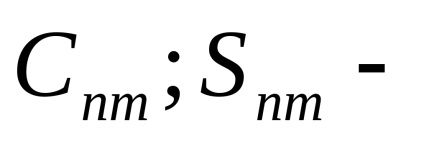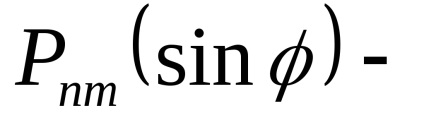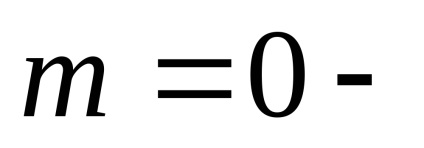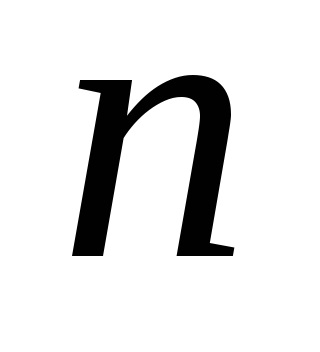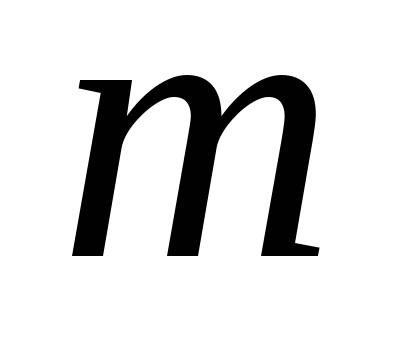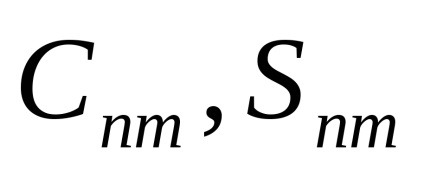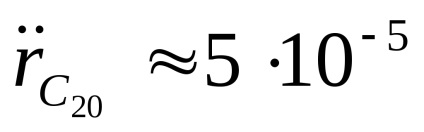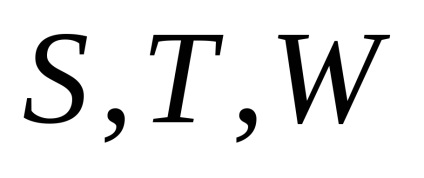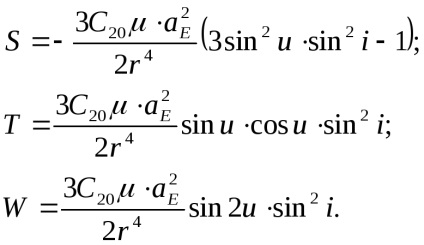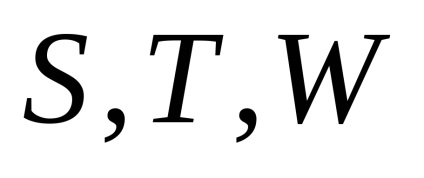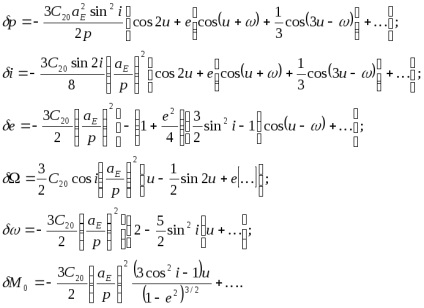Mai multe tipuri de perturbații de natură gravitațională și non-gravitațională acționează asupra sateliților sistemelor de radionavigație. Datorită faptului că sateliții se rotesc la o altitudine de aproximativ 20.000 km, influența radiației solare reflectate și rezistența la aer poate fi neglijată. De exemplu, forma neregulată și, în consecință, diferențele dintre secțiunile transversale ale sateliților complică modelarea presiunii radiației solare directe. Diferitele materiale utilizate pentru producerea de sateliți prezintă caracteristici diferite de absorbție a căldurii, ceea ce duce la dificultăți suplimentare atunci când se iau în considerare accelerațiile perturbatoare.
Influența accelerațiilor perturbe poate fi judecată prin următorul exemplu: permiteți-i să fie supus unei accelerații constante
posibilitatea. = 10-9 m / s 2. Deplasarea asociată cu eaîn poziția satelitului după dubla integrare în timpse obține caposibilitatea. . Înlocuirea cantității12 ore, obținem compensarea satelitului SRNS după o revoluție, care este egală cu≈ 1 m. Aceasta poate fi considerată o valoare tipică a deplasărilor.
Perturbarea potențialului gravitațional al Pământului.
Potențialul gravitațional al Pământului
pe un punct extern este posibil să se prezinte în forma:
,
unde
constanta gravitationala geocentrica;distanța geocentrică pentru punctul exterior;perturbând o parte a geopotențială. Primul termen din partea dreaptă determină mișcarea neperturbată (potențialul unei mingi sau punct), al doilea termen determină perturbații în mișcarea satelitului.
Potențialul de perturbare este dat de obicei sub forma unei extinderi într-o serie de funcții sferice:
,
unde
axa semimajor a Pământului;distanța geocentrică a satelitului;latitudinea și longitudinea. Valorilefără coeficienți fără dimensiuni care caracterizează câmpul gravitațional extern al Pământului. în cele din urmă,Legendre funcții (funcții sferice), care sunt împărțite în două tipuri:Legendre și funcțiile adiacente ale Legendre. numere întregișisunt gradul și ordinea extinderii.
Polinomii Legendre sunt definiți pe baza formulei Rodrigue:
,
pentru ei relația de recurență
.
Expresiile pentru primele două polinoame au forma:
Expresiile pentru funcțiile Legendre atașate sunt:
Funcții sferice sunt împărțite în zonale, sectoriale și tesseral (mozaic), în conformitate cu liniile de pe teren, care demarcate zona cu o varietate de caractere armonice.
Domenii de valori pozitive și negative:
a) în zonă; b) sectorial; c) pentru armonicile teșerale ale potențialului.
Coeficienții descompunerii armonice
sunt cunoscute din diferite modele potențiale. Cea mai mare influență asupra mișcării sateliților este legată de compresia ecuatorială a Pământului de către coeficientul celei de-a doua zone armonice. Valoarea maximă a accelerației perturbatoare datorată comprimării estecm ∙ s -2. Coeficienții rămași ai potențialelor armonici sunt de o mie de ori mai mici și, prin urmare, efectul pe care îl exercită este mai mic.
Funcția deranjantă a compresiei Pământului este scrisă ca:
Perturbații accelerații
sunt reprezentate de expresiile:
După înlocuire
o ecuație diferențială pentru elementele osculating orbitale și integrarea în prima apropiere, cu condiția ca r = 1, și toate elementele sunt constante, cu excepția în considerare, trei elemente obține perturbări asociate cu argumentul timp de latitudine sau:
În ultimele trei formule există perturbații legate în mod linear cu argumentul de latitudine
. Aceste perturbatii sunt numite seculare, și a spus trei elemente (longitudine, un argument de perigeul și înseamnă anomalie) în teoria perturbațiilor se numește elemente de colț. Perturbările cauzate de comprimarea pământului conduce la planul orbital de revoluție în jurul axei de rotație (orbita precesie) și care se rotesc în planul orbital. În elementele de poziționare, care includ inclinarea, excentricitatea și parametrul focal, există numai perturbații de compresie de scurtă perioadă.
În primii ani ai sistemelor de radionavigație prin satelit, un set de coeficienți până la cel de-al 8-lea ordin și grad a fost considerat suficient pentru sateliții pe arce la mai multe ture. În legătură cu cadrele de audit de referință pentru determinarea orbitele precise pentru modelele gravitația Pământului, folosind seturi de coeficienți cu numărul de ordine și puterea componentei multe zeci sau chiar sute.
Articole similare