TIPURI DE GRAFICĂ A COMPUTERULUI
Grafica grafică este o arie de informatică care studiază metodele și mijloacele de creare și prelucrare a imaginilor utilizând sisteme software și hardware de calcul. Grafica grafică este una dintre cele mai rapid dezvoltate ramuri ale științei informatice și, în multe cazuri, acționează ca o "locomotivă", tragând întreaga industrie a calculatoarelor în spatele ei.
Domenii de aplicare:
- medicina (tomografie computerizată);
- cercetarea științifică (vizualizarea structurii materiei, câmpurile vectoriale și alte date);
- modelarea țesăturilor și a hainelor;
- dezvoltarea dezvoltării etc.
În funcție de metoda de formare a imaginii, KG este împărțită în: bitmap, vector, fractal și 3D.
Pentru imaginile raster formate din puncte, conceptul de rezoluție, exprimând numărul de puncte pe unitate de lungime, este de o importanță deosebită. Ar trebui distins:
• rezoluția imaginii ecranului;
• Rezoluția imaginii imprimate.
Rezoluție originală. Rezoluția a punctelor originale pe inch (dotsper inch - dpi) și depinde de cerințele privind calitatea imaginii și dimensiunea fișierului, sau o metodă de metodă de creare ilustrația originală, formatul de fișier favorite și alți parametri digitizarea. În general, regula se aplică: cu cât cerințele de calitate sunt mai ridicate, cu atât este mai mare rezoluția originalului.
Rezoluția imaginii de pe ecran. Pentru copiile de pe ecran ale unei imagini, un punct elementar al unui raster este numit pixel. Dimensiunea pixelilor variază în funcție de rezoluția ecranului selectată (din intervalul standard), rezoluția originală și scala de afișare.
Monitoare pentru imagistica cu diagonala 20-21 (clase profesionale) furnizează de obicei un standard de 640x480 rezoluția ecranului, 800x600 pixeli, 1024x768, 1280x1024, 1600x1200, 1600x1280, 1920x1200, 1920x1600. Distanța dintre punctele învecinate ale fosforului într-un monitor de calitate este de 0,22-0,25 mm.
Rezoluția imaginii imprimate și conceptul de linie. Mărimea punctului de imagine bitmap pe ambele copii (hârtie, film etc.) și pe ecran depinde de metoda aplicată și de parametrii de rasterizare ai originalului. La rasterizare, originalul este suprapus cu o rețea de linii, ale căror celule formează un element raster. Frecventa grilei raster este masurata prin numarul de linii pe inch si se numeste linia.
Scalarea imaginilor raster. Unul dintre dezavantajele graficii raster este așa-numita pixelizare a imaginilor atunci când sunt mărite (dacă nu se iau măsuri speciale). Odată ce în original există un anumit număr de puncte, apoi la o scară mai mare, mărimea lor crește, elementele rasterului devin vizibile, ceea ce denaturează ilustrația însăși (figura 1). Pentru a contracara pixelizarea, este obișnuit să digitizați originalul în prealabil cu o rezoluție suficientă pentru o vizualizare de înaltă calitate, atunci când scalarea.
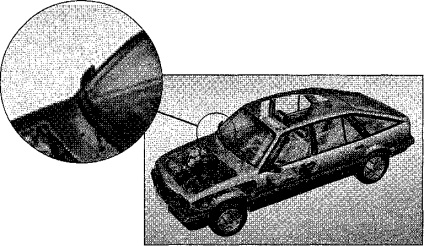
Fig. 1. Efectul de pixelizare la scalarea unei imagini bitmap
Dacă în graficul raster elementul de bază al imaginii este un punct, atunci în vectorul grafic există o linie. Linia este descrisă matematic ca un singur obiect și, prin urmare, cantitatea de date pentru a afișa obiectul utilizând grafică vectorială este semnificativ mai mică decât în grafica raster.
Linia este un obiect elementar al graficii vectoriale. Ca orice obiect, linia are proprietățile: forma (drept, curbă), grosimea, culoarea, inscripția (solidă, punctată). Liniile închise dobândesc proprietatea de umplere. Spațiul acoperit de acestea poate fi umplut cu alte obiecte sau cu o culoare selectată.
Cea mai simplă linie neînchisă este limitată de două puncte, numite noduri. Nodurile au, de asemenea, proprietăți ale căror parametri afectează forma capătului liniei și natura interfeței cu alte obiecte.
Toate celelalte obiecte de grafică vectorială sunt alcătuite din linii. De exemplu, un cub poate fi alcătuit din șase dreptunghiuri conectate, fiecare dintre ele fiind, la rândul său, formată din patru linii conectate. Este posibil să ne imaginăm un cub și ca douăsprezece linii conectate care formează coaste.
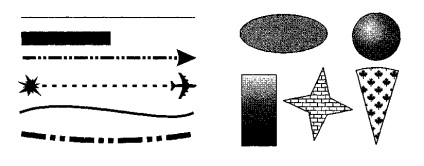
Fig. 2. Obiecte grafice vectoriale
Fundamente matematice ale graficii vectoriale
Să analizăm în detaliu metodele de reprezentare a diferitelor obiecte într-un grafic vectorial.
Punct. Acest obiect în plan este reprezentat de două numere (x, y) care indică poziția sa față de origine.
Linia dreaptă. Aceasta corespunde ecuației y = kx + b. Prin specificarea parametrilor k și b, puteți afișa întotdeauna o linie dreaptă infinită într-un sistem de coordonate cunoscut, adică doi parametri sunt suficienți pentru a specifica o linie.
Segmentul este drept. Aceasta diferă prin faptul că necesită încă doi parametri pentru a descrie - de exemplu, coordonatele xl și x2 ale începutului și sfârșitului segmentului.
Curba ordinii a doua. Această clasă de curbe include parabole, hiperbolași, elipse, cercuri, adică toate liniile ale căror ecuații conțin grade nu mai mari decât a doua. O curbă de ordinul doi nu are puncte de inflexiune. Liniile drepte sunt doar un caz special de curbe de ordinul doi. Formula curbei celei de-a doua ordini în formă generală poate arăta, de exemplu, după cum urmează:
Astfel, pentru a descrie o curbă infinită de ordinul doi, cinci parametri sunt suficienți. Dacă doriți să construiți un segment de curbă, aveți nevoie de doi parametri.
Curba este de ordinul trei. Diferența dintre aceste curbe și curbele de ordinul doi este prezența posibilă a unui punct de inflexiune. De exemplu, graficul funcției y = x? are un punct de inflexiune la origine (Figura 15.5). Această caracteristică face posibilă stabilirea curbelor de ordinul trei ca bază pentru cartografierea obiectelor naturale în grafica vectorială. De exemplu, liniile de încovoiere a corpului uman sunt foarte apropiate de cele ale ordinii a treia. Toate curbele de ordin secundar, cum ar fi cele directe, sunt cazuri particulare de curbe treilea ordin.
În cazul general, ecuația curbei treilea ordin poate fi scrisă ca:
Astfel, curba treilea ordin este descrisă de nouă parametri. Descrierea segmentului său va necesita încă doi parametri.
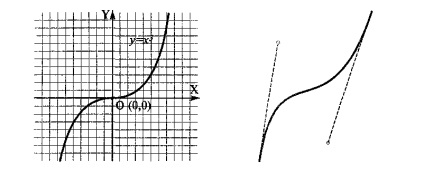
Fig. 3. Curba treia (în stânga) și curba Bezier (dreapta)
Bezier curbe. Acesta este un tip special, simplificat, de curbe treilea ordin. Metoda de construire a curbei Bezier se bazează pe utilizarea unei perechi de tangente atinse la segmentul de linie la capătul său. Segmentele curbelor Bezier sunt descrise de opt parametri, deci este mai convenabil să lucrați cu ei. Forma liniei este afectată de unghiul de înclinare al tangentei și de lungimea segmentului său. Astfel, tangentele joacă rolul de "pârghii" virtuale, prin care curba este controlată.