La soluția unei ecuații unidimensionale de undă neomogenă în formă finită
1 Universitatea Tehnică Ufa de Stat
În această lucrare propunem o metodă de integrare a unei ecuații unidimensionale a undelor neomogene pentru care soluția generală conține patru funcții arbitrare. Această idee se realizează atunci când se obține formula (7). Prezența a patru funcții arbitrare oferă oportunități ample de obținere a unei soluții atunci când există restricții asupra funcției dorite. Despre modul în care puteți dispune de aceste funcții este prezentat în exemplul unei probleme cu condiții limită inițiale și omogene. Solutia care cuprinde un număr finit de membri, numita soluție în formă închisă, spre deosebire de soluțiile convenționale de proces printr-o serie trigonometrică fără sfârșit. Ușor de soluții în formă finită se manifestă în calculele aproximative, în care nu este nevoie pentru a afla cum ar trebui să fie lăsat mulți membri ai seriei trigonometrice pentru a obține precizia necesară a soluției.
soluție în formă finită
1. Aramanovich I.G. și Levin VI Ecuații de fizică matematică. M. Nauka, 1964. - 288 p.
2. Korn G. Korn T. Manual de matematică pentru oamenii de știință și ingineri. M. Nauka, 1974. - 832 p.
3. NS Koshlyakov. Gliner E.B. Smirnov M.M. Ecuații în derivate parțiale ale fizicii matematice. M. Școala superioară, 1970. - 712 p.
4. Prudnikov A.P. Brychkov Yu.A. Marichev O.I. Integrale și serii. M. Nauka, 1981. - 800 p.
5. Tikhonov A.N. Samarskiy A.A. Ecuații de fizică matematică. M. Nauka, 1966. - 724 p.
În această lucrare se consideră o ecuație diferențială a formei
Descrie vibrațiile mici transversale, longitudinale și de torsiune ale unei tije omogene. Modul obișnuit de a rezolva o astfel de ecuație este de a găsi o soluție sub forma unei serii trigonometrice infinite [1, 3, 5]. În această lucrare propunem o metodă care oferă o soluție într-o formă finită.
1. În primul rând, găsim soluția generală a ecuației (1). Să trecem la noile variabile
Funcția va intra în funcție
,
și ecuația (1) conduce la formă
Integrarea ecuației (3) cu privire la o variabilă dă
unde sunt funcții arbitrare. Integrarea (5) obținem
unde sunt funcții arbitrare.
Să fie o funcție antiderivativă a lui În acest caz
și (6) pot fi scrise în formular
Înlocuind prin formule (2), obținem soluția generală a ecuației inițiale
2. Ca exemplu de aplicare a acestei metode, rezolvăm ecuația (1), în care luăm domeniul variației variabilelor
și condiții limită omogene
Completarea în (1) înlocuirea
obținem o ecuație cu forma (3):
a cărei soluție generală este dată de (7). Reprezentăm această ecuație în formă
Aceste egalități implică următoarele:
Prin urmare, din (8) obținem următoarea zonă de variație a variabilelor (figura):
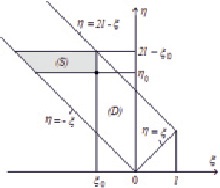
Banda nelimitată (D) este domeniul variației variabilelor ξ, μ (S) este regiunea adoptată ca regiune de integrare în integralele duble
În interior, luați un punct arbitrar și compilați graficul așa cum este arătat în figură. Această secțiune este dată de sistemul de inegalități
În conformitate cu (14), valoarea funcției în acest punct este
Domeniul de integrare este determinat de sistemul de inegalități
Prin arbitrarul de opțiuni, selectați-le, astfel încât sistemul de inegalități (17) coincide cu (16): Ecuația (14) ia forma
Realizăm condițiile (9) - (10) pentru a găsi funcțiile rămase u
Să scriem condițiile (9) - (10) în variabile folosind corespondența (15):
Jurnal științific ISSN 1812-7339 | ПИ №77-63397
Serviciul de asistență tehnică - [email protected]
Secretarul executiv al revistei Bizenkov M.N. - [email protected]
Materialele revistei sunt disponibile sub licența Creative Commons "Attribution" 4.0 World.