Articolul discută problema implementării componentelor definite în software în # xa0, o rețea deja existentă. Formularea problemei de optimizare a controlerului unei rețele definite de program și # xa0 este dată și o descriere matematică bazată pe un algoritm direct-dual.
Rețeaua definită de software # xa0; este ideologia clădirii rețelei, în # xa0; stratul de gestionare a rețelei și # xa0 sunt divizate și stratul de redirecționare a pachetelor. Metoda comună pentru toate abordările construirii de software definită este aceea că rețeaua definită de program constă din două componente principale:
- # xa0; Controlorul unei rețele definite de program (CS). CS este o funcție centralizată logic [1], [2]. Rețeaua este de obicei controlată de una sau mai multe CS-uri. CS determină calea de redirecționare pentru fiecare fir din rețeaua # xa0;
- # xa0; Element pentru transferul unei rețele definite de program (EP). EP-urile formează stratul de transmitere a datelor în rețeaua # xa0; Logica pentru transmiterea pachetelor este determinată de CS și # xa0; implementate în tabela de redirecționare # xa0;
Problema cu ingineria traficului este # xa0; că în scenariul probabil, componentele definite de program vor fi implementate treptat în # xa0; rețeaua deja existentă. În # xa0; o astfel de rețea nu este neapărat tot traficul este controlat de un CS. Pot exista mai multe CS-uri pentru diferite părți ale rețelei și, de asemenea, unele părți ale rețelei pot utiliza ruta existentă în rețeaua # xa0; Întrebarea cheie este # xa0; ce altceva se poate face eficient în gestionarea traficului # xa0, atunci când tot traficul din rețeaua # xa0; nu poate fi administrat centralizat de un CC.
Rețeaua în discuție conține un CS central care calculează tabelele de rutare pentru un număr de EP-uri. Se presupune că EP-urile sunt un subset de noduri din rețeaua # xa0; Nodurile rămase din rețelele # xa0; rulează un protocol standard de rutare hop-by-hop (de exemplu, OSPF). CS scanează rețeaua și # xa0; colectează informații despre starea linkului # xa0; Routingul pachetelor EP și # xa0; logica pentru calculul tabelului de rutare pe EP este în CS centralizat # xa0; În plus față de transmiterea de pachete # xa0, EP efectuează unele măsurători de trafic simple care sunt transmise către CS. CS utilizează aceste informații # xa0; traficul cu # xa0, informațiile difuzate în # xa0; rețea # xa0, folosind protocolul OSPF-TE pentru a modifica dinamic tabelele de rutare de pe EP cu # xa0, pentru a se adapta la # xa0; schimbare condițiile de trafic. Nodurile de rețea convenționale sunt routere standard utilizând un mecanism comun de rutare hop-by-hop [3]. Se presupune că nu vor fi aduse modificări la # xa0, nodurile ordinare și # xa0, ei nu pot să știu despre # xa0; existența în EP # xa0; rețea.
Un exemplu de rețea cu elemente de redirecționare # xa0; CS și # xa0; este prezentat în Fig. 1. Elementele de transmitere în # xa0; nodurile 2, 9, 14 sunt controlate de CC din exterior. Această rețea va fi utilizată pentru a ilustra conceptele prezentate în # xa0; această lucrare. Pentru simplitate, presupunem că toate conexiunile din rețele sunt bidirecționale și greutatea liniilor de comunicație este setată la # xa0; una. Acum descriem CS și EP mai detaliat.
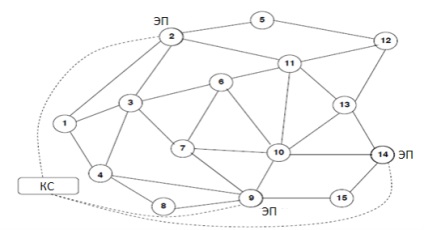
1.1 Elementul de transfer al unei rețele definite de program
EP îndeplinește următoarele funcții:
Transmitere: EP-urile funcționează în # xa0, în cea mai mare parte în # xa0; calitatea elementelor de rutare. Tabelul de rutare este calculat pe CS [4]. EP poate procesa următoarele tranziții pentru un anumit nod de destinație. Dacă există mai multe tranziții următoare la acest nod de destinație, EP poate împărți traficul în destinația # xa0; în ordinea # xa0; presetate în următoarele câteva noduri.
1.2 Controler de rețea programabil
CS efectuează toate logica de rutare și # xa0; coordonează rutarea la toate EP-urile pentru a obține cea mai bună performanță a rețelei. COP îndeplinește următoarele funcții:
Calculul rutei: CS este responsabil pentru calcularea tabelelor de rutare pentru toate ES în rețeaua # xa0; Calculul are loc cu # xa0, ținând seama de ruta efectuată în unități convenționale (pe baza greutăților liniilor de comunicație OSPF), traficul de pe liniile de comunicare (pe baza unui OSPF-TE) și # xa0; modelul de trafic curent (pe baza măsurătorilor la FL). Algoritmul de calcul al rutei pentru EP ar trebui să asigure că rutarea va avea loc pe căi fără bucle, reducând în același timp congestia rețelei.
2. Declarația privind misiunea COP
Să ilustrăm câteva dintre conceptele prezentate în # xa0; paragraful anterior, folosind Fig. 2. Presupunem că toate greutățile sunt egale cu una și # xa0; comunicare continua sunt drumul minim la # xa0; nodul 13. Reamintim că nodurile 2, 9, 14 sunt EP. Trebuie remarcat faptul că NH (6, 13) = 10, NH (1, 13) = 2 și # xa0; Linile punctate prezintă posibile căi alternative din EP. De exemplu, asamblarea 2 poate fi împărțit traficul la nodul 13 prin intermediul a două tranziții diferite, unul merge la nodul 5, și # xa0, pe un alt nod 11.
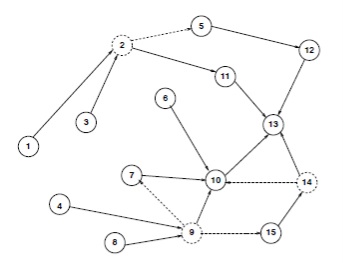
Fig. 2. Arborele celor mai scurte căi spre nodul 13
Definiția 1: C # xa0; luând în considerare setul din C # xa0; EP, calea s = u0, u1, u2. = n # xa0; din nodul sursă s # xa0; la nodul de destinație d # xa0; va fi numit executabil dacă pentru j = 1,2. k, (uj-1, uj) ∈ E # xa0;
Calea executabilă, unde u0, u1, u2. uk sunt diferite, numite mod admisibil. Denumim Psd ca set de căi admisibile între s # xa0 și d.
Din definiție rezultă că calea este posibilă dacă următoarea tranziție la # xa0; un nod de destinație dat pentru toate elementele de rețea obișnuite este dată de algoritmul pentru găsirea celei mai scurte căi. În plus, calea executabilă este validă numai în absența buclelor. Prin urmare, trebuie să vă asigurați că tot traficul dintre s # xa0; și d # xa0; trebuie să fie redirecționat către P ∈ Psd.
De exemplu, în Fig. 2, 3-2-5-12-13 este o cale validă de la 3 la 13. Rețineți că aceasta nu este calea cea mai scurtă care este 3-2-11-13. Calea 3-6-11-13 nu este permisă, deoarece următorul pas pentru nodul 3, care nu este un EP, ar trebui să fie următorul pas de-a lungul celei mai scurte căi care este nodul 2.
Definiția 2: Având în vedere cea mai scurtă cale de rutare pe un nod normal, traficul care trece de la sursă la # xa0; destinația fără tranzit prin EP va fi numită necontrolată. Dacă sursa pachetului este EP sau dacă trece prin cel puțin un EP înainte de a ajunge la destinație, atunci acest trafic va fi numit controlat.
Cu alte cuvinte, traficul controlat constă în pachete care trec prin cel puțin un EP. De exemplu, traficul de la 6 la 13 este direcționat către OSPF la 6-10-13 și # xa0, deoarece nici 6, nici 10 nu sunt EP-uri, traficul de la nodul 6 la nodul 13 nu este monitorizat. În cazul # xa0, spre deosebire de aceasta, traficul de la nodul 8 la 13 trece prin nodul 9, care este EP și, prin urmare, acest trafic este monitorizat.
Definiția 3: Spunem că un CE u∈C introduce un pachet dacă
- # xa0; Nodul u # xa0; se află în calea de rutare OSPF pentru pachet;
- # xa0; Pachetul trece prin u # xa0, înainte de a trece prin orice alt EP.
Traficul, care este introdus cu # xa0; folosind UE u ∈ C # xa0; pentru un nod de destinație, d ∈ N, numim Iud.
Prin urmare, pentru toate traficurile monitorizate, există un EP unic care introduce acest trafic. Să explicăm acest lucru în Fig. 3. În această figură, numărul de lângă # xa0; nod reprezintă rata de trafic de la nodul la # xa0; nodul 13. De exemplu, traficul de la nodul 1 la # xa0; nodul 13 (T1,13) este de 3 unități. Prin definiție, numărul de trafic de la 3 la 13 va fi introdus cu # xa0; utilizând EP-2. De exemplu, în figura 3, I2,13 = 9, I9,13 = 13 și # xa0; I14,13 = 5. Așa cum anterior menționat, valorile nu sunt cunoscute COP Tsd. Măsurătorile disponibile pe CS sunt valorile Wud, care reprezintă traficul pentru destinația d care trece prin nodul u ∈ C.
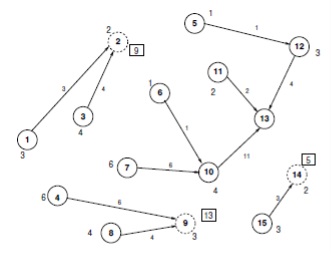
Fig. 3. Trafic independent către EP
3. Formularea problemei COP
Deoarece traficul care trece prin EP este controlat, este necesar să se țină seama de traficul introdus la PE. Iudul de trafic, introdus pe EP u ∈ C, trebuie să ajungă la destinația d. Acest lucru este posibil numai pentru una dintre căile admisibile P ∈ Pud. . Fie g (e) reprezintă fluxul neghidat pe linia e obiectivul este construirea COP monitorizat traseu de trafic astfel încât întârzierea și # xa0; pierderea de pachete pe linia sunt ținute la # xa0; minim. Unul dintre obiectivele naturale pentru COP este de a minimiza utilizarea maximă a conexiunilor în # xa0; Rețea (x (P) # xa0; - flux în # xa0; calea P):
- # xa0; Primul set de inegalități arată că debitul total al relației, care este suma fluxului necontrolat (reprezentat prin ascendent g (e)) și # xa0 controlată de flux (care este al doilea termen al sumei de pe partea dreapta) este mai mică decât produsul de utilizare maximă a liniilor de comunicație ( θ) asupra debitului legăturii de comunicație (c (e));
- # xa0; Al doilea set de inegalități indică faptul că traficul de intrare total este direcționat către # xa0;
- # xa0; Al treilea set de inegalități asigură faptul că fluxul pe orice cale nu este negativ.
Valoarea optimă a lui θ este utilizarea maximă a oricărei conexiuni. Dacă valoarea optimă a θ <1, то ни одна из связей не будет использоваться чрезмерно. После того, как КС решает эту задачу оптимизации, то легко вычислить следующие переходы и соответствующие веса во всех ЭП для каждого пункта назначения.
În declarația de mai sus, sa presupus că sunt cunoscute valorile lui Iud și ale lui (e). De fapt, ambele valori ale IUD și # xa0 și g (f) trebuie calculată cu # xa0, prin COP pe baza măsurătorilor efectuate de EPO și # xa0; de asemenea, mesajul de protocol OSPF-TE, obținut prin COP.
3.1 Calculul dinamic Iud și # xa0; g (e)
Valorile măsurate disponibile pentru CS sunt
- # xa0; Sarcina de legătură f (e) pentru toate referințele e ∈ E, care poate fi obținută de la OSPF-TE.
- # xa0; Valoarea lui Wud pentru toate u ∈ C # xa0; pentru toate d ∈ N. Aceasta este măsurată prin EP și # xa0; transmisă la # xa0; CS.
Folosind aceste două valori, CS trebuie să calculeze valorile g (e) pentru toate e ∈ E # xa0 și Iud pentru toate u ∈ C # xa0; pentru toate d ∈ N. Mai întâi, Iud trebuie calculat. Luați în considerare un nod țintă fix d. CS cunoaște ruta curentă la # xa0; acest nod de destinație d. El cunoaște toate tranzițiile următoare pentru toate nodurile d # xa0 și pentru toate EE-urile, dar nu cunoaște toate tranzițiile următoare la destinația și distribuția traficului # xa0; dacă există mai multe opțiuni de rută.
Definiție 4: Având în vedere un nod destinație d # xa0, iar curentul de rutare # xa0; Procedura de rutare rețea uzlovv # xa0 C în raport cu această d # xa0 este definit ca ordonarea nodurilor din # xa0; C \ D # xa0, astfel încât, dacă u ∈ C # xa0; apare înainte de v ∈ C # xa0; în această listă, nu există alt fir al cărui destinație d este de la v # xa0; Notăm ordinea de rutare către nodul destinație d # xa0, ca R (d) și # xa0; faptul că u # xa0; apare înainte de a v # xa0; în R (d) modul în care u ≺d v.
Această ordine de rutare este definită corect pentru orice nod țintă d, deoarece nu pot exista bucle în # xa0; o rută de trafic care trece prin destinația d. Să presupunem că rutarea curentă către nodul # xa0 are loc așa cum se arată în Fig. 4. Se reflectă numai partea din ruta care se referă la # xa0; EP. În acest caz, trebuie să fiti atenți că traficul de la nodul 9 trece prin nodul 14. Prin urmare, 9 ≺13 14. O ordine de rutare (2, 9, 14). Sunt posibile și alte ordonări, dar apoi nodul 14 ar trebui să apară după nodul 9.
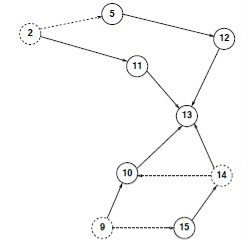
Algoritmul pentru calculul valorii Iud
Pentru fiecare nod de destinație, d ∈ N
- # xa0; Calculați ordinea de rutare R (d);
- # xa0; Pentru primul nod u # xa0; în R (d), setați Iud = Wud;
- # xa0; Construiți prima cale de curgere de la u # xa0; la d # xa0 și setați βv (u, d) ca parte a fluxului care ajunge la nodul v ∈ C;
- # xa0; Pentru fiecare nod ulterior w # xa0; în R (d). Setați Construiți prima rută de flux de la w # xa0; la d # xa0 și setați βv (w, d) pentru toate v ∈ C.
După valorile IUD sunt cunoscute pentru toate u ∈ C # xa0; pentru orice d ∈ N, este necesară calcularea valorilor g (e), care este necontrolată de trecere a traficului de-a lungul liniei de e ∈ E. Aceasta se face după cum urmează: curentul este introdus în unitatea # xa0; nod u ∈ C # xa0; pentru scopul d ∈ N # xa0 ;. și αe (u, d) se calculează, care face parte dintr-un singur flux, care este transmis la linia e Deoarece IUD cunoscut pentru u ∈ C, poate fi calcula
CS-ul cunoaște acum valorile lui Iud pentru toate nodurile u ∈ C # xa0; pentru toate d ∈ N și # xa0; de asemenea, valorile lui g (e) pentru toate e ∈ E.
3.2 Formularea problemei rutei dinamice
Este necesar să se traseze traficul CS pentru a minimiza utilizarea maximă a legăturilor din rețeaua # xa0; O problemă echivalentă, care este mai ușor de rezolvat, este să setați lățimea de bandă a unei linii fixe, dar să modificați traficul de intrare astfel încât acesta să fie încă localizat în rețeaua # xa0; Această problemă apare în # xa0; următoarele:
Dacă optimal λ> 1, atunci traficul curent poate fi trimis către EP, asigurându-se în același timp că toate comunicațiile sunt mai puțin de o singură cale de utilizare. În ciuda faptului că problema are un număr exponențial de variabile, este posibilă rezolvarea problemei la orice nivel de precizie dorit, folosind un algoritm direct-dual.
Pentru a scrie un program liniar (decizie) pentru problema dinamică de rutare prezentat mai sus, este necesar să se lege variabilele duale l (e) o # xa0; canal de comunicare și de lățime de bandă # xa0; ZUD pentru a limita cererea. Un algoritm direct-dual poate fi acum scris în # xa0;
Presupun (e) este setat ca o legătură de greutate e ∈ E. Lud notat ca cea mai scurtă cale de la u # xa0; la d # xa0 ;. Cu conexiuni greutăți l (e) link e-dreapta dublu algoritm poate fi acum rescrisă în formularul # xa0;
Cu alte cuvinte, ținând seama de orice set de greutăți de legătură l (e), care nu este negativ, este limita superioară din # xa0; problema de rutare dinamică.
În această lucrare am examinat problema implementării componentelor definite în software în # xa0; o rețea existentă. Problema administratorului unei rețele definite de program a fost formulată și # xa0; noțiunile unei căi controlate fezabile, executabile și # xa0; introducerea traficului în # xa0; rețea și # xa0; De asemenea, este prezentată formularea problemei de rutare dinamică pe controlerul unei rețele definite de program și # xa0, descrierea ei matematică pe baza unui algoritm direct-dual.
Termeni de bază (generați automat). nodul destinație, CE în rețeaua de rutare VC, destinație d, tabele de rutare, ordinea de rutare, existența EPO în rețea, un număr de VC, tabela de rutare, o multitudine de EPO prin EPO, EPO cu scop, PE și alte noduri EPO ar trebui un EP unic, o tabelă standard de rutare, o tabelă de rutare, un nod de destinație, rutarea traficului către CS, mai multe CS-uri.