În combinatorie, o combinație de elemente distincte N în M este o colecție de elemente M selectate din setul de elemente N. Aceste seturi diferă numai în ceea ce privește apariția elementelor specifice M în ele, ordinea elementelor dintr-un astfel de set nu este importantă. Seturile care diferă numai în ordinea elementelor (dar nu și în compoziție) sunt considerate a fi identice, iar aceste combinații sunt diferite de destinațiile de plasare.
Combinații fără repetări
Sarcina. Găsiți toate combinațiile posibile fără repetiții din setul de elemente cu 2.
Există următoarele combinații:
Numărul de combinații posibile fără repetiția elementelor N peste M poate fi determinat prin formula (N≥M):
că în M! ori mai puțin decât numărul corespunzător de plasări fără repetări (deoarece combinațiile fără repetiții nu depind de ordinea elementelor).
Considerăm problema obținerii tuturor combinațiilor pentru numerele 1. N față de M.
Implementarea în C ++
#include
folosind namespace std;
bool NextSet (int * a, int n, int m)
int k = m;
pentru (int i = k - 1; i> = 0; - i)
dacă (a [i]
pentru (int j = i + 1;
return true;
>
return false;
>
void Print (int * a, int n)
static int num = 1;
cout.width (3);
cout <
int main ()
int n, m, * a;
cout <<"N = " ;
cin >> n;
cout <<"M = " ;
cin >> m;
a = nou int [n];
pentru (int i = 0; i
Imprimare (a, m);
dacă (n> = m)
în timp ce (NextSet (a, n, m))
Imprimare (a, m);
>
cin.get (); cin.get ();
retur 0;
>
Combinații cu repetări
Combinațiile cu repetări sunt numite seturi de elemente M în care fiecare element al setului N poate participa de mai multe ori. În același timp, nu se impun restricții asupra raportului dintre valorile lui M și N, iar numărul total de combinații cu repetări este
Un exemplu al unei astfel de probleme este alegerea cărților poștale M din N în toate modurile posibile.
Pentru a genera combinații cu repetiții, hai să folosim soluția pentru generarea de destinații de plasare cu repetări, luate în considerare în acest articol.
Implementarea în C ++
#include
folosind namespace std;
bool NextSet (int * a, int n, int m)
int j = m-1;
în timp ce (a [j] == n j> = 0) j-;
dacă (j <0) return false;
dacă (a [j]> = n)
j--;
a [j] ++;
dacă (j == m - 1) returnează adevărat;
pentru (int k = j + 1; k
return true;
>
void Print (int * a, int n)
static int num = 1;
cout.width (3);
cout <
int main ()
int n, m, * a;
cout <<"N = " ;
cin >> n;
cout <<"M = " ;
cin >> m;
int h = n> m. n. m; // mărimea matricei a este aleasă ca max (n, m)
a = int int [h];
pentru (int i = 0; i
Imprimare (a, m);
în timp ce (NextSet (a, n, m))
Imprimare (a, m);
cin.get (); cin.get ();
retur 0;
>
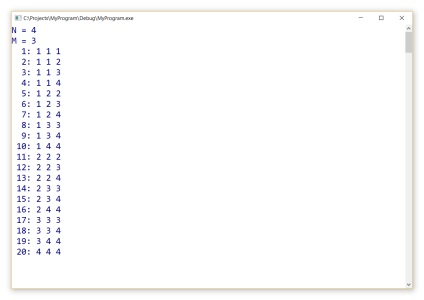
Rezultatul algoritmului de mai sus: