Informații istorice despre polyhedra obișnuită ............... .. ... .9
Poliedra dreapta din jurul nostru ..................................... 14
Tema "Polyhedra" este una dintre cele mai importante din cursul tradițional al geometriei școlare. Acestea constituie, se poate spune, subiectul central al stereometriei. Studiul liniilor și planuri ale unghiurilor diedre paralele și perpendiculare, iar cealaltă, precum și introducerea vectorilor și coordonate - toate acestea sunt doar începutul geometriei solide, instrumente de pregătire pentru studiul obiectelor sale mai semnificative - mai ales solide și suprafețe.
Rolul central al polyhedra este determinat în primul rând de faptul că multe rezultate legate de alte organisme sunt obținute din rezultatele corespunzătoare pentru polyhedra; Este suficient să reamintim definirea volumului de corpuri și suprafețe de suprafețe trecând la limită din polyhedra.
În plus, polyhedra ei înșiși reprezintă un subiect extrem de informativ de cercetare, prezentând printre toate corpurile cu multe proprietăți interesante, legate în mod special de teoremele și problemele acestora. Se poate revedea, de exemplu, teorema lui Euler privind numărul de fețe, muchii și vârfuri, simetria polihedra obișnuită, chestiunea umplerii spațiului cu polihedra,
Poliedre trebuie administrat într-un curs de școală mai multă atenție, de asemenea, deoarece acestea oferă un material deosebit de bogat pentru dezvoltarea de concepte spațiale pentru dezvoltarea imaginației spațiale a legăturii de viață cu logica strictă, care este esența geometriei. Deja faptele cele mai de bază despre poliedre necesită o astfel de conexiune, care se dovedește a fi nu foarte ușor. Chiar și un astfel de fapt simplu, ca intersecție a diagonalelor cutiei la un moment dat, necesită un efort de imaginație pentru a vedea în mod clar, și necesită dovezi stricte.
Mai mult decât atât, utilizarea polyhedra de la începutul studiului de stereometrie servește diferite scopuri didactice. Pe polyhedra este convenabil să se demonstreze aranjamentul reciproc al liniilor drepte și a planurilor în spațiu, pentru a arăta aplicarea de semne de paralelism și perpendicularitate a liniilor drepte și a planurilor în spațiu. Ilustrarea primelor teoreme ale stereometriei asupra modelelor specifice ridică interesul studenților față de subiect.
De asemenea, una dintre principalele sarcini ale predării matematicii este dezvoltarea gândirii abstracte în studenți. Acest obiectiv este facilitat în mare măsură de folosirea mijloacelor vizuale, nu numai în clasele junior, ci și în seniori. Tema "Polyhedra", în special, producția independentă de ajutoare vizuale de către studenți, oferă oportunități ample pentru realizarea acestui scop. În procesul de fabricare a modelelor de polyhedra, pe lângă cunoștințele și abilitățile teoretice, elevii consolidează noile concepte create cu ajutorul unui desen și al soluționării efective a problemelor de construcție. Când creați modele, imaginea este creată în părți, astfel încât să puteți efectua diferite manipulări cu ele. În același timp, toate proprietățile și caracteristicile lor sunt ușor de recunoscut și fixate ferm în memoria elevilor.
Un polyhedron este un corp geometric, delimitat pe toate laturile de poligoane plane, numite fețe.
Latura fețelor sunt marginile polyhedronului, iar capetele muchiilor sunt vârfurile polyhedronului. Numarul de fete se distinge prin tetraedra, pentahedra etc.
Un polytope este considerat a fi convex dacă este situat tot pe o parte a planului. fiecare dintre fețele sale.
Un poliedru convex se numește regulat dacă toate fețele sale - poligoane regulate același converge același număr de muchii și fețele adiacente formează unghiuri egale la fiecare nod.
Figura prezintă un tetraedru, hexaedru, octaedron, dodecaedru și icosaedron. Forma lor este un exemplu de perfecțiune! Și de ce este dată poliedra potrivită un astfel de nume? Ce caracteristici au? Cum sa faci un model de polyhedron obisnuit? Unde puteți întâlni aceste corpuri uimitoare?
Răspundeți la aceste întrebări și la alte întrebări: scopul acestei lucrări.
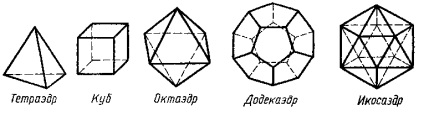
Toate polyhedra obișnuite au un număr diferit de fețe și numele sunt obținute din acest număr.
Tetraedrul (din tetra, patru și hedrale grecești, este o față) este alcătuit din 4 triunghiuri regulate, la fiecare vârf 3 margini se întâlnesc.
Hexahedron (din greacă "hexa" - șase și "hedra" - fațetă) are 6 fețe pătrate, la fiecare vârf 3 margini se întâlnesc.
Hexaedrul este mai bine cunoscut ca un cub (din latina "cubus", din greaca "kubos".
Octaedronul (din octul grec - opt și hedra - față) are 8 fețe (triunghiulare), la fiecare vertex 4 marginile converg.
Dodecaedrul (din dodeka grecească - doisprezece și hedra-fațet) are 12 fețe (pentagonale), la fiecare vârf 3 margini se întâlnesc.
Icoședronul (din eikosi grecești - douăzeci și hedra - față) are 20 de fețe (triunghiulare), la fiecare vârf 5 marginile converg. (5, p. 267-269)
Se pare că există exact cinci polihedra obișnuite - nu mai mult și nici mai puțin. La urma urmei, pentru a obține un polyhedron obișnuit, în fiecare vârf, conform definiției sale, același număr de fețe trebuie să se converge, fiecare dintre ele fiind un poligon obișnuit.
Suma unghiurilor plane ale unghiului poliederic trebuie să fie mai mică de 360 °. altfel nici o suprafață poliedrică nu va funcționa. Luarea soluțiilor integrale posibile ale inegalităților: 60k
Poliedra corectă în jurul nostru.
În carte, începutul biolog german al acestui secol, Haeckel „Kunstformen der Natur“, puteți citi următoarele linii: „Natura ei, le în sânul ei un număr inepuizabil de creaturi minunate, care frumusețea și varietatea depășesc cu mult toate formele de arta umane create“ Deci, de exemplu, organisme unicelulare phaeodarians au forma unui icosahedron.
Un alt fapt interesant este că acesta este un icosaedru a devenit centrul atenției de biologi în disputele lor cu privire la forma de viruși. Virusul nu poate fi complet rotund, așa cum sa crezut anterior. Pentru a instala forma, lua o varietate de poliedre, lumina îndreptate asupra lor la aceleași unghiuri ca fluxul de atomi la virus. Sa dovedit că doar un singur polyhedron dă exact aceeași umbra - un icosaedru. Proprietățile sale geometrice, menționate mai sus, permit salvarea informațiilor genetice. Poliedrele potrivite sunt cifrele cele mai profitabile. Iar natura o folosește pe scară largă. Cristalele unor substanțe care ne sunt cunoscute au formă de polihedra obișnuită. Astfel, forma de cristal cubic transmite sare NaCl, monocristal alaun de potasiu din aluminiu are forma unui octaedru, pirita sulf FeS cristal are forma unui dodecaedru, sulfat de sodiu surmenisty - tetraedrul, bor - icosahedron.
Dacă puneți pe glob centrele celor mai mari și mai remarcabile culturi și civilizații ale lumii antice, puteți vedea regularitatea în locația lor față de polii geografici și ecuatorul planetei. Multe depozite de minerale se întind de-a lungul grila icosahedron-dodecahedron. Mai multe lucruri uimitoare se întâmplă la intersecția acestor coaste: aici sunt centrele culturilor și civilizațiilor străvechi: Peru, Mongolia de Nord, Haiti, cultura Ob și altele. În aceste puncte, se observă maxime și minime ale presiunii atmosferice, vânturile uriașe ale Oceanului Mondial, aici Loch Ness scoțian, Triunghiul Bermudelor. Studiile ulterioare ale Pământului, probabil, vor determina atitudinea față de această frumoasă ipoteză științifică, în care aparent, poliedra corectă ocupă un loc important. (2, p.2)
Lucrarea de cercetare a fost interesantă și variată și a făcut clar faptul că lumea din jurul nostru este supusă legilor geometriei.
Ca parte a lucrării asupra rezumatului, a fost studiată literatura de specialitate, s-au descoperit trăsăturile polyhedra obișnuite, desenele, machetele, modelele de polyhedra obișnuite.
Poliedrului în spațiul tridimensional, setul de un număr finit de poligoane plane, astfel încât fiecare parte a fiecăruia dintre poligoane este în același timp, cealaltă parte (dar numai unul), numit adiacent primului (pe această parte); din oricare dintre poligoanele care alcătuiesc polyedronul. Puteți merge la oricare dintre ele, merge la adiacente acesteia, și de la aceasta, la rândul său, - .. la adiacente, etc. Aceste poligoane sunt numite fețe, laturile lor - muchii și vârfuri lor - vârfurile poliedru.
Lumea noastră este plină de simetrie. Din cele mai vechi timpuri, ea se referă la înțelegerea noastră a frumuseții. Poate că acest lucru explică interesul continuu al omului pentru polihedra corectă - simboluri uimitoare ale simetriei care au atras atenția multor gânditori remarcabili, de la Platon și Euclid la Euler și Cauchy.
Forma elementului principal al Pământului - cubul, aer - octaedru, Foc - tetraedrul, Apa - icosaedru, și creatorul lumii a dat forma un dodecaedru pentagonala. Pitagoreenii au învățat că Pământul are forma unei sfere. Potrivit lui Pitagoras, există 5 figuri corporale: divinitatea superioară a construit universul pe baza formei geometrice a dodecaedrului. Pământul este ca Universul, iar Pământul lui Platon este și un dodecaedru.
Matematica greacă, în care a apărut pentru prima dată teoria polyhedra, sa dezvoltat sub marea influență a celebrului gânditor Platon.
Platon (427-347 î.Hr.) - marele filozof grec, fondator al Academiei și fondatorul tradiției platonismului. Una dintre trăsăturile esențiale ale învățăturii sale este luarea în considerare a obiectelor ideale - abstractizări. Matematica, după ce a adoptat ideile lui Platon, din vremea Euclidului studiază exact obiectele abstracte și ideale. Cu toate acestea, el însuși Platon, și multe dintre matematicii antice investite în termen ideală nu este numai un sens abstract, dar sensul cel mai bun. În conformitate cu tradiția merge înapoi la matematicieni antice, printre cele mai bune din toate poliedre sunt cei care au fețele lor poligoane regulate.
Teoria polyhedra este una dintre secțiunile fascinante și izbitoare ale matematicii. În abstractul prezentat, doar o parte din această teorie a fost luată în considerare. Din poliedre regulate - solidele platonice - se poate obține așa-numitele poliedre semi-regulat, sau solidele Arhimede, ale căror fețe sunt, de asemenea, corecte, dar poligoanele și stea corpul opuse de dreapta.
1. Dorofeev G.V. Peterson L.G. Matematica. Gradul 6. Partea 3 - M: Balass, 1988.