Momentele axiale și centrifuge de inerție în raport cu axele care trec prin centrul de greutate al secțiunii transversale a tijei sunt uneori numite momente de inerție adecvate.
Prin ce formula se calculează momentele de inerție ale figurii față de axa paralelă cu cea centrală? Ce momente de inerție sunt numite portabile?
Fie ca două axe reciproce perpendiculare x și y să treacă prin centrul de greutate C al secțiunii transversale a tijei. Desenați celelalte axe de coordonate
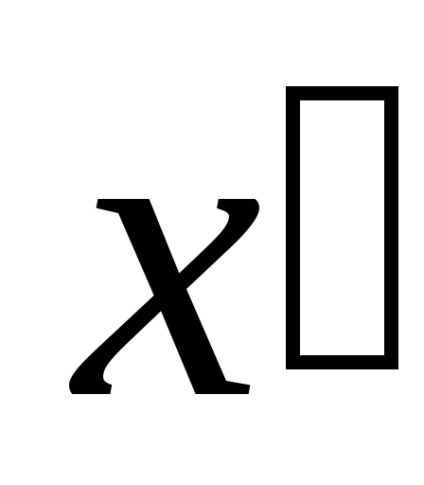

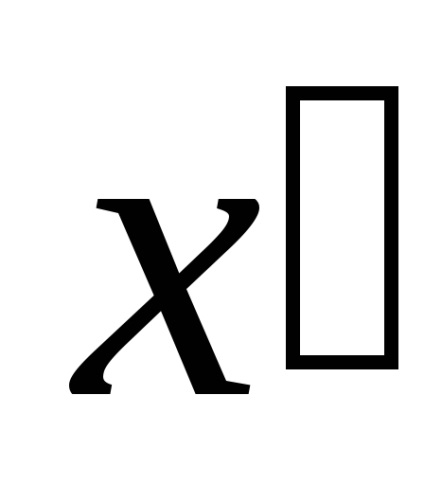

T
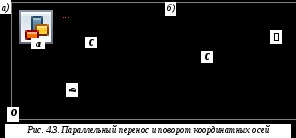
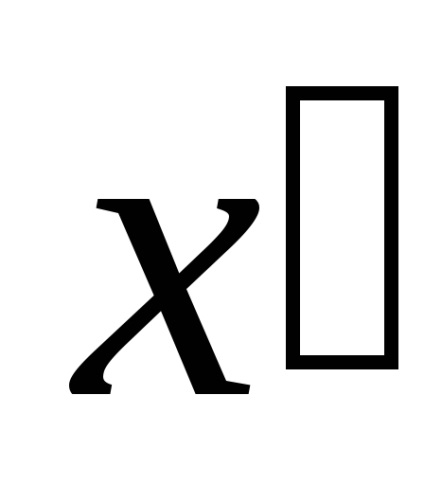

Primii termeni din aceste formule au fost numiți anterior de către noi momentele de inerție adecvate. Al doilea termen (subliniat) din formula (4.6) se numește momentele de transport ale inerției.
Rețineți că coordonatele a și b trebuie înlocuite cu formulele (4.6) cu semnele lor luate în considerare. care este extrem de important pentru a treia dintre aceste formule.
Cum schimbă momentele inerțiale corecte atunci când axele coordonatelor sunt rotite?
Spuneți-ne propriile momente de inerție
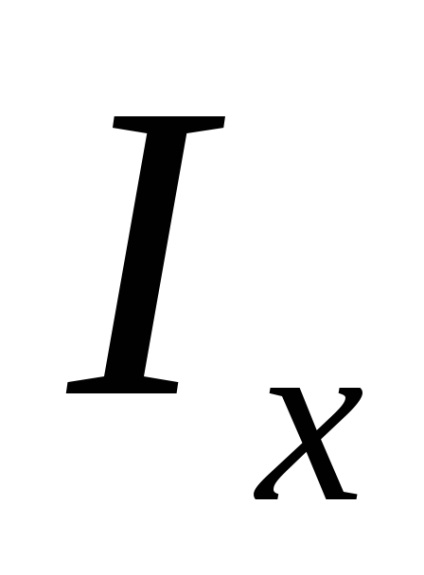
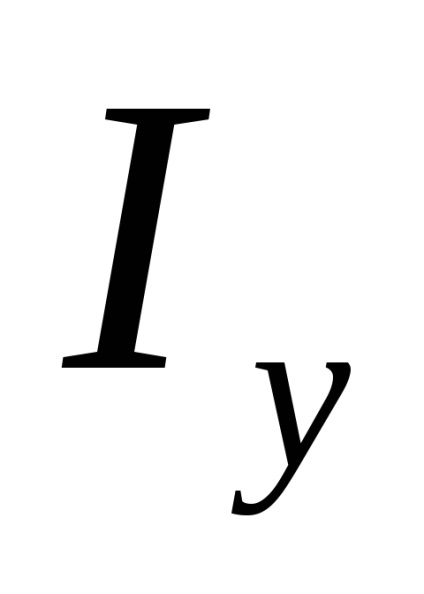
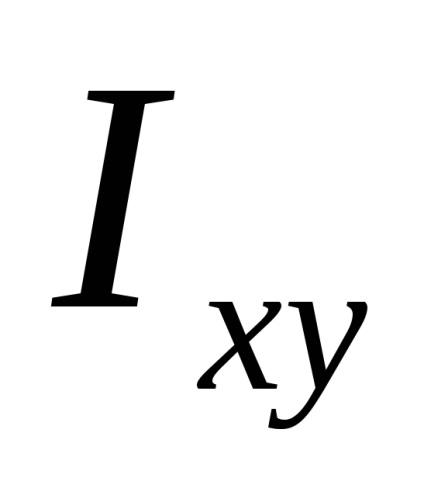
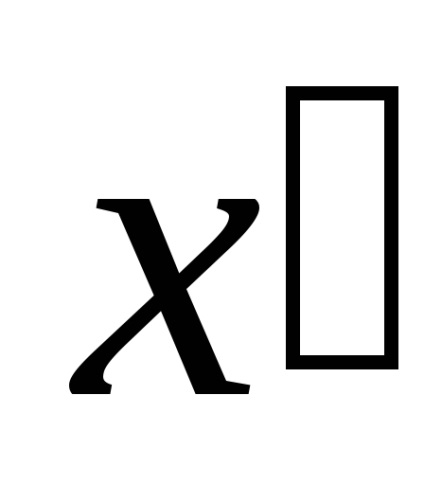


Apoi momentele de inerție a secțiunii transversale în ceea ce privește noile direcții sunt determinate de formule:
;
.
Se vede din (4.7) că
,
adică suma propriilor momente axiale de inerție este o valoare constantă (nu se modifică atunci când axele coordonatelor sunt rotite).
După cum sa menționat mai sus, cele două axe perpendiculare între ele care trece prin centrul de greutate al figurii, cu privire la care momentul de inerție centrifugal este zero, numit axele centrale principale de inerție. Apoi, cu
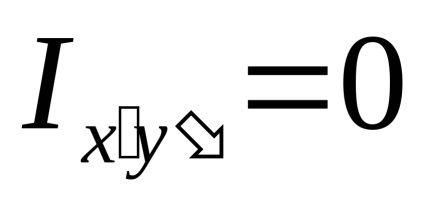
Din expresia rezultantă (4.8) găsim două valori ale unghiului
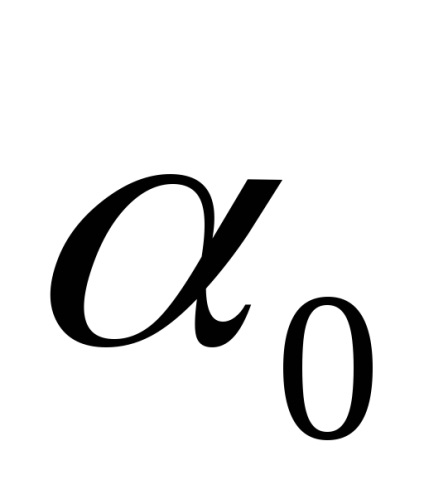

Ce momente axiale de inerție sunt numite principalele momente de inerție?
Cu rotația axelor centrale și apropierea lor de axele centrale principale, cea mai mare dintre propriile momente axiale de inerție devine și mai mare, ținând cont de valoarea maximă
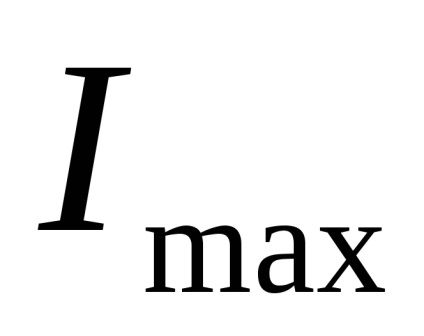
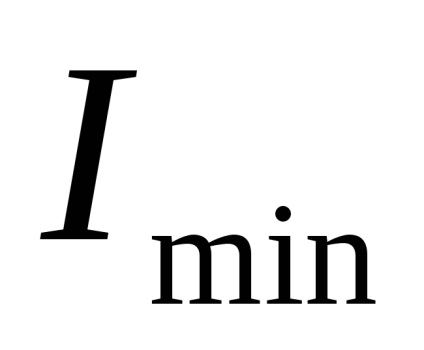
Momente de inerție a figurii față de axele centrale principale
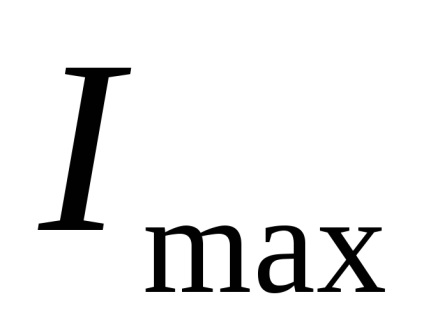
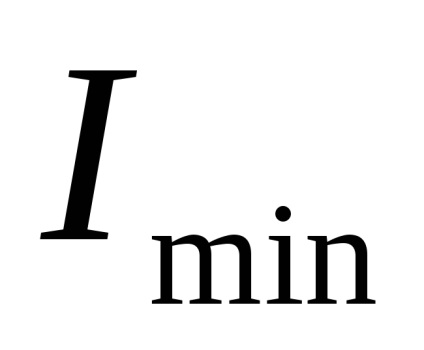
Observăm o proprietate importantă care rezultă din aceste formule. Dacă în cazul special
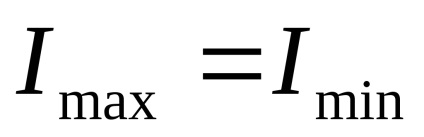
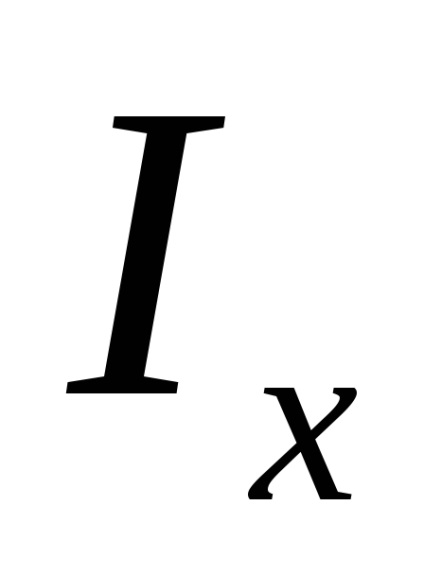
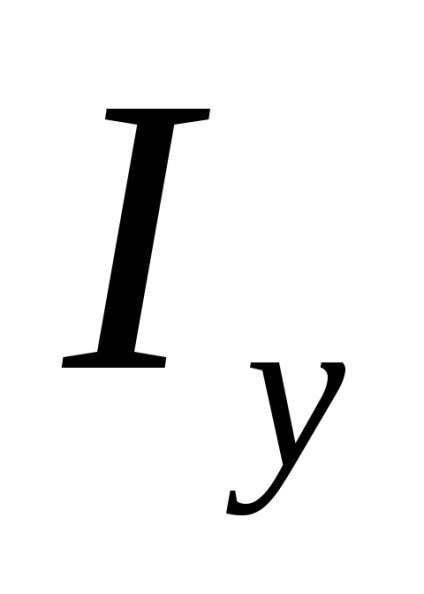
În ceea ce privește o figură complexă, determinați care dintre axele centrale principale este axa max, adică axa în raport cu care momentul de inerție își asumă cea mai mare valoare?
Prin definiție, momentul axial al inerției este egal cu integralitatea produselor din zonele elementare de către pătratul distanțelor lor față de axa corespunzătoare. Prin urmare, cu cât mai multe locații sunt îndepărtate de pe axă și cu cât mai multe astfel de situri, cu atât este mai mare momentul de inerție axial.