Aici și - deformarea și unghiul de rotație la începutul sistemului de coordonate, originea este întotdeauna situat la partea extrema stângă a fasciculului;
Z - distanța de la origine la secțiunea în care se determină deformarea și unghiul de rotație;
a, c, c, d este distanța de la origine la punctul de aplicare a forțelor externe corespunzătoare m, p, q.
METODA DE MOOR - VERESHCHAGINA
Pentru acest construct moment încovoietor unei sarcini exterioare predeterminată (vezi Figura 43, precum și.) Printr-o forță de unitate (figura 43b). Pentru determinarea deflexie și unitatea momentului - (. Figura 43B) Pentru calcularea unghiului de rotație, și este produs „multiplicare“ diagrame corespunzătoare , și anume dintr-o diagramă luăm zona ei. iar pe de altă parte - ordonata. dispusă sub centrul de greutate al zonei luate.
Reguli de bază pentru multiplicarea diagramelor:
- rezultatul este pozitiv dacă diagramele sunt situate pe o parte a axei fasciculului, dacă pe părți opuse - rezultatul este negativ;
- rezultatul pozitiv al multiplicării diagramelor indică faptul că direcția de deplasare (liniară și unghiulară) coincide cu direcția forțelor unitare, cu un rezultat negativ - opus direcției forțelor unitare;
- dacă ambele diagrame (și) sunt lineare, atunci nu contează din care diagrame să desenezi zona. cu care ordonați;
- dacă una dintre curbe este curbilinară (aceasta), atunci zona trebuie luată din ea;
- dacă este dificil să se calculeze suprafața diagramei, se determină coordonatele centrului de greutate al acesteia și ordonată. atunci când se înmulțesc diagramele și se folosește metoda Simson (formula 28) (Figura 44).
A, B, C - ordonate din diagrama de transport de marfă
a, b, c - și dintr-o singură diagramă
- partea din spate a secțiunii i a fasciculului
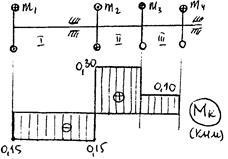
1. Determinați valoarea momentelor externe de răsucire, înainte de fiecare rolă (prin puterea și viteza arborelui)
unde N - putere, kW; n este numărul de rotații pe minut.
2. Construim complotul de cuplu, spărgând arborele în secțiunile I, II, III, aplicând metoda secțiunii și adopind următoarea regulă de semne pentru cuplul
dacă se uită la partea din stânga a arborelui din partea secțiunii, atunci
Diagrama arată că în secțiunile unde se aplică momente externe, se obțin salturi egale în mărime cu aceste momente. Valoarea maximă
3. Se determină diametrul arborelui termenilor de rezistență și rigiditate, aplicând formula (20) predetermina forfecare admisibilă
aici tradus în
Din valorile obținute, luăm diametrul axului d = 35 mm, asigurând astfel cerințele și rigiditatea și rezistența.
PROBLEMA № 33. Pentru un suport pas dat încărcate okruchivaet momente externe m1 = 10, m2 = kNm și 30 kNm și prinsă la ambele capete, este necesar pentru a construi un cuplu epure Mk și atunci când este permis de forfecare [] = 80. Definirea diametrele părțile solide și inelare (Figura 46). Partea inelară D = 2d, d0 = 0,8d, r. F. C = = 0,4
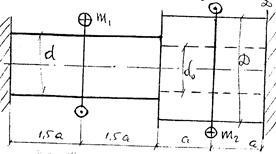
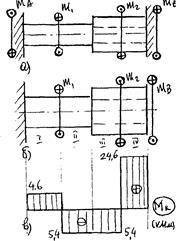
Noi îl transformăm într-unul determinat static, renunțând de exemplu la suportul "B", înlocuind acțiunea sa cu momentul de referință "m". Aruncând suportul "B", am făcut posibilă întoarcerea secțiunii transversale B sub influența tuturor momentelor externe, dar de fapt, într-un sistem dat, secțiunea B este fixată rigid, nu are o întoarcere. Vom reflecta acest fapt, după ce am făcut ecuația deplasărilor:
Folosind legea lui Hooke pentru torsiune, scriem
După ce am redus "a" și rigiditatea "", ajungem
Aici u sunt momentele polare ale inerției părților solide și inelare ale suportului. Raportul lor este
Rezolvând ecuația (31), obținem valoarea momentului de referință
Apoi, din ecuația de echilibru, determinăm valoarea momentului de referință
Valorile pozitive obținute ale momentelor de sprijin și indică faptul că direcția lor a fost aleasă corect.
2. Împărțim sistemul dat în secțiunile I, II, III, IV (figura 47b). Limitele secțiunilor sunt secțiuni în care se aplică momente externe și se modifică secțiunea transversală. Construim diagramele momentului cuplului (figura 47c) folosind metoda secțiunii
3. Din starea rezistenței la torsiune și definesc diametrelor părți ale suportului inelar continuu sunt predeterminate ca o funcție mai mare forfecare
Astfel, cele mai mari tensiuni tangențiale acționează în valorile celor două secțiuni și sunt comparate cu cele admise
Prin urmare, diametrul părții solide d este
Apoi dimensiunile părții inelare a brațului vor fi.
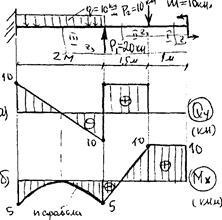
1. Introducem construcția diagramelor și M de-a lungul secțiunilor spre dreapta, din partea capătului liber (fig.48a și b)
Se determină coordonatele secțiunii transversale, unde forța transversală trece prin zero, în această secțiune momentul de încovoiere are o valoare extremă
2. Din condiția rezistenței pe o curbă dreaptă, determinăm dimensiunile (numărul canalului) secțiunii fasciculului.
Conform sortimentului pe canalul GOST 8240 - 82 [1] și considerând că secțiunea constă din canale, luăm canalul nr. 10, care.
Cere grinzi simplu rezemate construi diagrame de forțe transversale și momente de încovoiere și definesc cu o marjă de siguranță va funcționa (fig. 49), în cazul în care b = 60 mm, h = 140 mm, a = 35 mm.
1. În primul rând, determinăm reacțiile de suport din starea de echilibru a fasciculului
Prin urmare, reacțiile sunt determinate corect.
2. Rupem fasciculul în secțiunile I, II, III, IV, limitele secțiunilor sunt secțiuni în care se aplică forțe externe. Folosind metoda secțiunii, vom compila diagramele și (figurile 49a și b)
a treia secțiune (ia în considerare partea dreaptă);
3. Din diagrama vedem că cel mai mare moment de încovoiere este de 20 kNm.
4. Calculați valoarea tensiunilor maxime normale care acționează în fasciculul cu ajutorul formulei (22), care a determinat în prealabil momentul axial al rezistenței unei secțiuni transversale date prin intermediul momentului axial al inerției
5. Rezistența fasciculului este determinată de condițiile de rezistență
; . care este suficient.
Pentru un anumit fascicul I (Figura 50), diagrame și. ridica secțiune la = 160 MPa și verifica rezistența forfecare, precum și pentru a determina deformarea în punctul „C“, secțiune transversală, iar unghiul de rotație „K“ prin două metode: o metodă de parametrii inițiali și de Ocean - Vereshchagin.
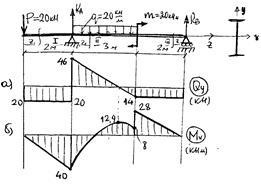
2. Construiți diagramele și. prin secțiuni (figurile 50a și b)
coordonarea secțiunii, unde
3. Selectăm secțiunea fasciculului I al fasciculului din starea de rezistență în funcție de solicitările normale. de aici.
Conform sortimentului GOST 8239 - 89, acceptăm fasciculul nr. 22a, care. . .
4. Aplicăm secțiunea aleasă la efortul de forfecare folosind tensiunile tangențiale. Zhukovsky.
Stresul de forfecare admisibil este de obicei egal cu
În consecință, rezistența tensiunilor tangențiale este pe deplin asigurată, deoarece
5. Definiți deflecția "" în, t "C" și unghiul de rotație al secțiunii "K" (în exemplul nostru coincid) prin metoda parametrilor inițiali. Pentru a face acest lucru, plasăm originea în secțiunea extremă din stânga și scrieți
În această ecuație, ambii parametri inițiali sunt necunoscuți. Pentru a le determina, vom forma ecuațiile de deformări pentru secțiunile de deasupra suporturilor A și B, unde este clar că ele sunt egale cu 0.
Înlocuind valorile coordonatelor și forțelor externe, obținem două ecuații
Rezolvându-le, ajungem
Apoi deflecția secțiunii "C" va fi egală cu
Unghi de rotație a aceleiași secțiuni
6. Se determină secțiunea deflexie „C“, secțiunea transversală și unghiul de rotație „K“ de Mohr - Vereshchagin, pentru acest plus față de diagrama momentelor de încovoiere ale unei sarcină (. Figura 51a) și să construiască diagrame singură concentrație (51 și) și produc multiplicare diagramele corespunzătoare. Rezultatul (vezi alin. 28 de exprimare) deflexie
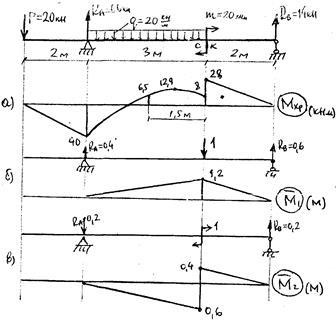
adică, au obținut practic aceeași valoare de deviere cu metoda parametrilor inițiale.
de asemenea, practic a coincis cu valoarea obținută prin metoda parametrilor inițiali.
O valoare are ca rezultat pozitiv multiplicatoare diagramele arată că deplasările unghiulare ale secțiunilor liniare și „C“ și „K“ coincide cu direcția rezistenței unității (îndoire în jos și răsucire în sens orar).
VARIANTELE SARCINILOR PRIME
Tema de casă № 3 intră în sarcinile de decizie 2 și o sarcină de torsiune directe de îndoire. Număr sarcini de circuit de calcul și de date de intrare, în conformitate cu propriile sale unul luat din tabelele № 3 (prima problemă), № 4 (a doua problemă) și № 5 (3 - lea sarcină).
Când faci temele este obligatorie!
- a construi un complot al cuplului;
- determină diametrele unei secțiuni circulară solidă sau inelară a condițiilor de rezistență și rigiditate sau a stresului maxim de forfecare și a factorului de siguranță "K";
În a doua sarcină:
- pentru a dezvălui indeterminarea statică a sistemului dat, pentru a compila numărul necesar de ecuații de deplasare;
- a construi un complot al cuplului;
- din condițiile de rezistență determină diametrele necesare pentru o anumită secțiune a tijei.
- pentru a construi diagramele forțelor transversale și momentelor de îndoire M pentru fascicul;
- să aleagă din condițiile de rezistență dimensiunile secțiunii transversale a formei date;
- determină deformarea în secțiunea „C“, secțiune transversală, iar unghiul de rotație „K“ de parametrii inițiali ai metodei și Mohr - Vereshchagin.