Prezentare pe tema: "Cycloid 1 Curba descrisă de un punct fixat pe un cerc de rulare de-a lungul unei linii drepte se numește cicloid. - Transcriere:
1 Cicloid 1 Curba descrisă de un punct fixat pe un cerc care se rotește de-a lungul unei linii drepte se numește cicloid. Pentru imaginea cicloidă, complotăm pe linie un segment AB egal cu circumferința, adică AB = 2πR. Împărțim acest segment în 8 părți egale cu punctele A 1. A 8 = B. Aflați unde va fi punctul A marcat atunci când cercul de rulare de-a lungul unei linii drepte ajunge la punctul B?

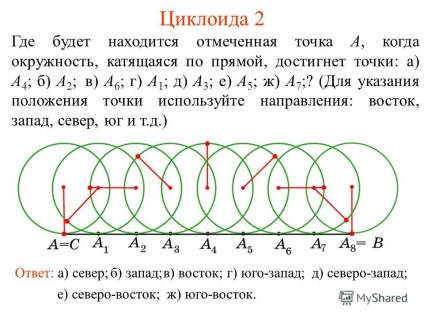
2 Cicloid 2 În cazul în care punctul marcat A va fi situat, atunci când un cerc de rulare de-a lungul unei linii drepte ajunge la punctul: a) A 4; b) A2; c) A6; d) A1; e) A3; (e) A5; g) A7; (Pentru a indica locul punctului, folosiți direcțiile: est, vest, nord, sud etc.) Răspuns: a) nord, b) vest, c) est, d) sud-vest; (e) Nord-Est, (g) Sud-Est.
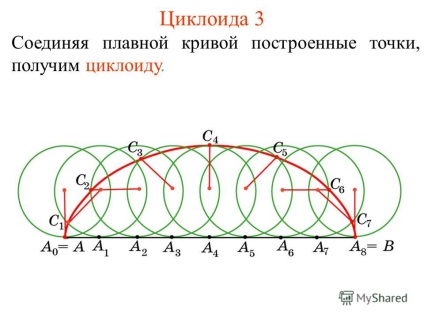
3 Cicloid 3 Conectând curba netedă a punctelor construite, obținem un cicloid.
4 Cycloid în mișcare Primul care a studiat cicloidul a fost Galileo Galilei (1564 - 1642). De asemenea, el a venit cu numele său.

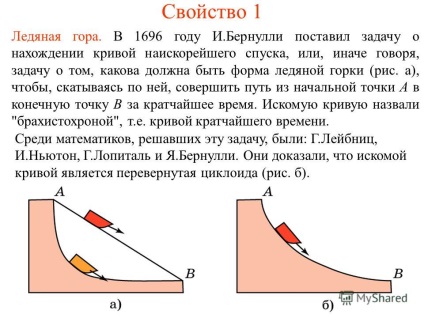
5 Proprietate 1 Ice Mountain. În 1696, J. Bernoulli a pus problema de a găsi cea mai abruptă curba de coborâre, sau cu alte cuvinte, problema a ceea ce ar trebui să fie sub formă de slide-uri de gheață (fig. A), astfel încât alunecarea pe el, pentru a face o cale din punct de plecare A la punctul final În cel mai scurt timp. Curba cerută a fost numită "brahistochrom", adică curba celui mai scurt timp. Printre matematicienii care au rezolvat această problemă au fost: G. Leibniz, I. Newton, G. Lopital și J. Bernoulli. Ei au demonstrat că curba dorită este un cicloid inversat (figura b).
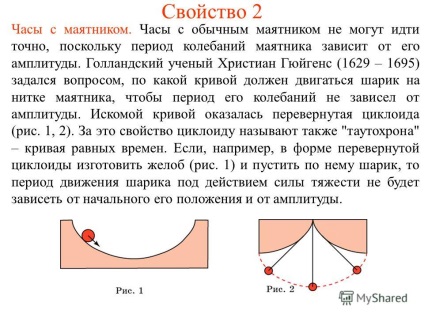
6 Proprietate 2 Un ceas cu un pendul. Un ceas cu pendul ordinar nu poate merge exact, deoarece perioada de oscilație a pendulului depinde de amplitudinea lui. om de știință olandez Christiaan Huygens (1629 - 1695) se întreba la ce curba trebuie să se miște mingea pe un șir de pendulului la perioada de oscilație este independentă de amplitudinea. Curba dorită a fost un cicloid inversat (Figura 1, 2). Pentru această proprietate cicloidul este numit și "tautochrona" - o curbă de timp egal. Dacă, de exemplu, sub forma unui Realizați jgheab cicloida inversat (fig. 1) și pune-l pe minge, perioada de mișcare mingea sub influența gravitației nu va depinde de poziția inițială și de amplitudinea sa.
7 Exercițiul 1 Cercul de rază 1 se rotește de-a lungul unei linii drepte. La ce distanță de această linie vor exista puncte C 1, ..., C 7. Răspuns. 1. 2. 1.

8 Exercițiul 2 Cicloidul are: a) axele de simetrie; b) centrul simetriei? Răspuns: a) Da, b) nu.
9 curba cicloida Elongated, care descrie punctul fixat la extinderea razei cercului de rulare de-a lungul unei linii numite cicloida extinse.
11 curba cicloidă redusă, care descrie punctul fixat pe raza interioară a cercului de rulare de-a lungul unei linii drepte, numite scurtat cicloidă.
13 Exercițiul 1 Trageți traiectoria vârfului triunghiului drept, rulând în linie dreaptă.
14 Exercițiul 2 Trageți o traiectorie a vârfului unui pătrat de rulare în linie dreaptă.
15 Exercițiul 3 Desenați o traiectorie a vârfului unei rulete hexagonale regulate în linie dreaptă.
16 Cardioidul 1 Traiectoria mișcării unui punct fixat pe un cerc care se rotește în afara unui alt cerc de aceeași rază se numește un cardioid. Răspunsul este: a) vest; b) est; c) est, d) sud, e) nord; (e) Sud, (g) Nord. Pentru imaginea unui cardioid, împărțiți cercul în 8 părți egale cu punctele A 1. A 8 = B. Aflați unde va fi punctul A marcat atunci când cercul de rulare de-a lungul unei linii drepte ajunge la punctul: a) A 4; b) A2; c) A6; d) A1; e) A3; (e) A5; g) A 7.
17 Cardioid 2 Conectând curba netedă a punctelor construite, obținem un cardioid.
18 Cardioid în mișcare
19 Exercițiul 1 Cardioidul are: a) axele de simetrie; b) centrul simetriei? Răspuns: a) Da, b) nu.
20 Exercițiul 2 Trageți traiectoria vârfului triunghiului drept rulant pe un alt triunghi regulat.
21 Exercițiul 3 Trageți o traiectorie a vârfului unui pătrat care se rostogolește în afara unui alt pătrat.
22 Exercițiul 4 Desenați o traiectorie a mișcării vârfurilor unui hexagon obișnuit care se rotește în afara celuilalt hexagon obișnuit.
23 Cardioid extins Traiectoria mișcării unui punct fixat pe extensia razei unui cerc care se rotește de-a lungul unui alt cerc cu aceeași rază se numește un cardioid alungit. Desenați această curbă.
25 Cardioidul scurtat Traiectoria mișcării unui punct fixat pe o rază în interiorul unui cerc care se rotește de-a lungul unui alt cerc de aceeași rază se numește un cardioid scurtat. Desenați această curbă.
27 Astrode Traiectoria mișcării unui punct fixat pe un cerc care se rotește în alt cerc de 4 ori raza se numește astroid. Desenați această curbă.
29 Exercițiul 1 Are astroidul: a) axele de simetrie; b) centrul simetriei? Răspuns: a) Da, b) da.
30 Exercițiul 2 Trageți o traiectorie a părții superioare a pătratului cu partea 1 rulând pe interiorul unui alt pătrat cu fața 4.
31 Astroidul alungit Traiectoria mișcării unui punct fixat pe prelungirea razei unui cerc de rulare în alt cerc de 4 ori raza se numește astroid alungit. Desenați această curbă.
33 Steiner Curve Traiectoria mișcării unui punct fixat pe un cerc care se rotește într-un cerc diferit de 3 ori raza se numește o curbă Steiner. Desenați această curbă.
35 Steiner curbă alungită traiectoria unui punct fix pe raza extensie a răsucirii cerc în interiorul altui cerc cu raza de 3 ori mai mare se numește o curbă alungită Steiner. Desenați această curbă.
36 Curba alungită Steiner
37 Epicicloid Curba descrisă de un punct fixat pe un cerc care se rotește în afara unui alt cerc se numește epicicloid. Raportul dintre raze poate fi diferit. Desenați un epicicloid în cazul în care raportul dintre raze este 2: 3.
39 Epicicloidul alungit Curba descrisă de un punct fixat la continuarea razei unui cerc care se rotește în afara celeilalte circumferințe este numit epicycloid alungit. Raportul dintre raze poate fi diferit. Desenați un epicicloid alungit în cazul în care raportul dintre raze este 2: 3.
41 Epicicloidul scurtat Curba descrisă de un punct fixat pe raza unui cerc care se rotește în afara celuilalt cerc este numit epicycloid scurtat. Raportul dintre raze poate fi diferit. Desenați un epicycloid scurtat în cazul în care raportul dintre raze este 2: 3.
43 Hipocicloidă O curbă care este descrisă de un punct fixat pe un cerc care se rotește în interiorul unui alt cerc se numește hipocicloid. Raportul dintre raze poate fi diferit. Desenați un hipocicloid atunci când raportul dintre raze este 2: 5.
45 Exercițiul 1 Desenați o cale de mișcare a unui punct fixat pe un cerc care se rotește afară pe celălalt cerc dacă raportul dintre raze este 1: 2.
46 Exercițiul 2 Desenați o cale de mișcare a unui punct fixat pe un cerc care se rotește în afara celuilalt cerc dacă raportul dintre raze este 2: 1.
47 Exercitarea 3 Desenați o cale a unui punct fixat pe un cerc care se rotește din exteriorul celuilalt cerc, dacă raportul dintre raze este 2: 5.
48 Exercitarea 4 Desenați o cale a unui punct fixat pe un cerc care se rotește de două ori mai mare în celălalt cerc. Curba în mișcare Răspuns: Diametrul cercului.
49 Exercitarea 5 Dovada că diametrul căii unui punct fixat pe un cerc care se rostogolește într-un alt cerc de două ori raza este o traiectorie. Soluție: Să se deplaseze cercul de rulare de la punctul B la punctul D, iar P să fie centrul său. Indicați prin C punctul de intersecție al diametrului AB cu acest cerc. Apoi, unghiul CPD este de două ori mai mare decât unghiul BOD. Prin urmare, arcele BD și CD-ul sunt egale, adică C este punctul fixat pe cercul de rulare.