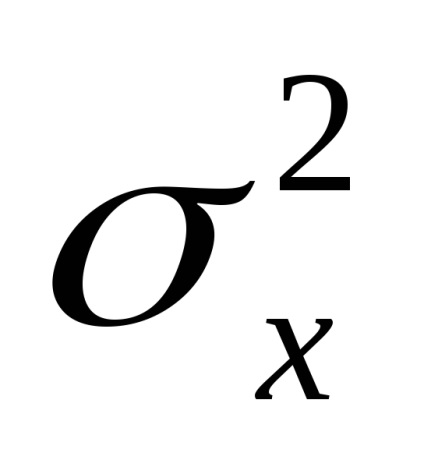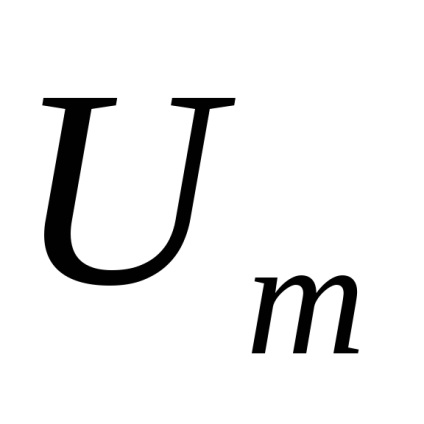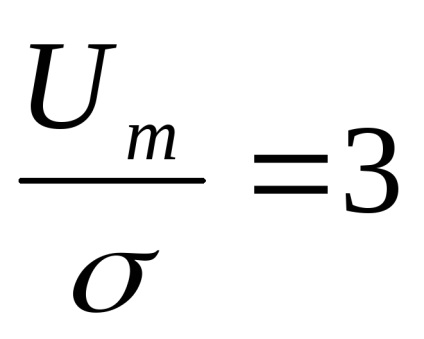un proces randomizat staționar, cu o constantă spectrală a densității de putere la toate frecvențele, se numește zgomot alb.
Prin teorema Wiener-Khinchin, funcția de corelare a zgomotului alb:
este egal cu zero peste tot, cu excepția punctului
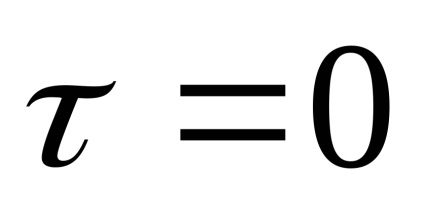
Zgomotul alb este un proces corelat cu delta. Necorespunzarea valorilor instantanee ale unui astfel de semnal aleator înseamnă o rată infinit de mare de schimbare în timp, indiferent cât de mic este intervalul

Zgomotul alb este un model matematic abstract și procesul fizic care îi corespunde cu siguranță nu există în natură. Cu toate acestea, acest lucru nu interferează cu înlocuirea aproximativ reale procese de zgomot alb aleatoare suficient de bandă largă în cazurile când circuitul de transmisie de bandă, care afectează semnalul aleator este lățimea efectivă substanțial mai îngustă a spectrului de zgomot.
B) Distribuția Gaussiană (normală).
În teoria semnalelor aleatoare, densitatea de probabilitate Gaussian este de importanță fundamentală.
conținând doi parametri numerici m și
Schimbare variabilă
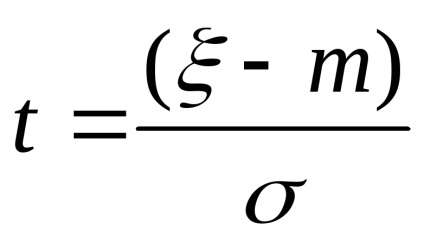
Aici $ este probabilitatea integrală
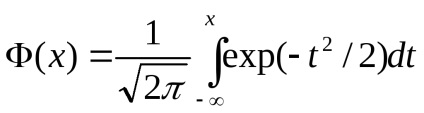
Graficul grafic al funcției F (x) are forma unei curbe monotonice variind de la 0 la 1.
16 .. Procesul de bandă îngustă aleatorie. Distribuție Rayleigh. Legea Rayleigh-Rice.
Să investigăm proprietățile semnalelor aleatorii în bandă îngustă, în care densitatea spectrală a puterii are un maxim pronunțat aproape de o anumită frecvență
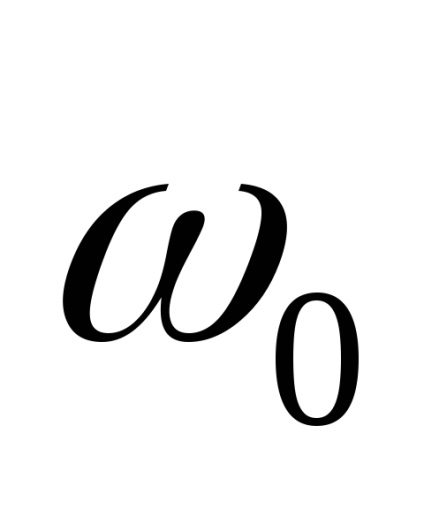
Să considerăm un proces aleatoriu staționar x (t), spectrul de putere unilaterală al acestuia
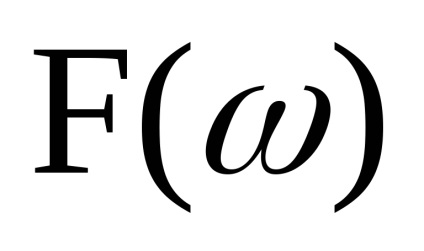
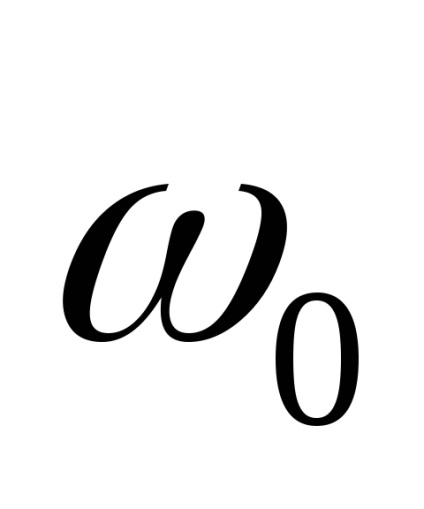
trecem spectrul procesului din vecinătatea frecvenței
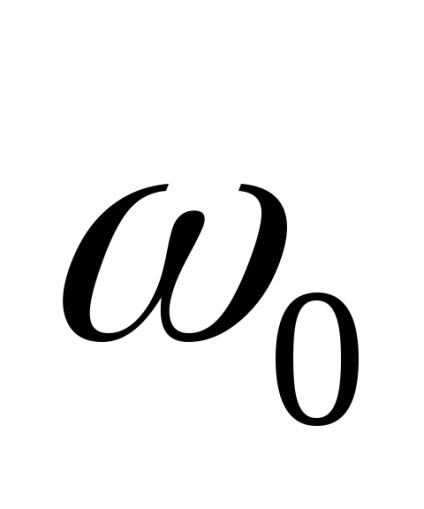
Prin medierea cu densitatea de probabilitate (7.22), găsim valoarea medie a plicului și varianța lui:
Cu plicului densitate de probabilitate de o-dimensionale, puteți rezolva o serie de probleme în teoria proceselor aleatoare de bandă îngustă, în special, găsiți probabilitatea de a depăși un anumit nivel al plicului.
Variabile aleatoare distribuite conform legii Rayleigh.
Cea mai simplă sarcină este de a găsi densitatea unidimensională de probabilitate a anvelopei de înveliș a oscilației totale. Presupunând că semnalul util, în timp ce zgomotul, scrie expresia pentru realizarea procesului total X (t). Acest proces aleatoriu este îngust, deci implementarea sa poate fi exprimată prin schimbarea lentă a învelișului U (t) și a fazei inițiale
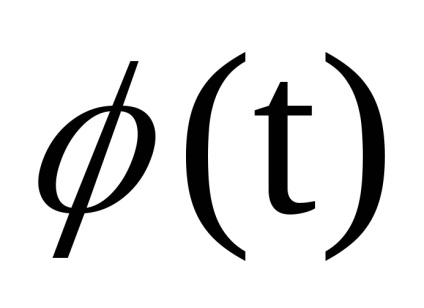
În noile variabile pe care le avem.
Acum, pentru a obține un plic cu densitate unidimensional probabilitate trebuie să se integreze în partea dreaptă a formulei (7.26) la unghiular de coordonate prin care am găsit:
Această formulă exprimă legea, care a fost numită legea Rice. Observăm când
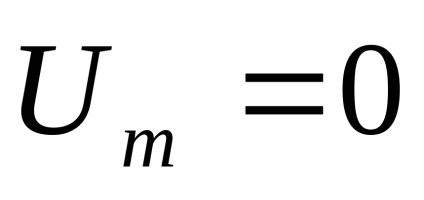
Înlocuind această expresie în (7.27), avem
Ie Plicul semnalului rezultat este apoi distribuit aproximativ în mod normal cu varianța