Această pagină este propusă a fi fuzionată cu Farmhouse Point.
Punctele Torricelli sunt două puncte din care toate laturile triunghiului sunt vizibile fie sub un unghi de 60 °, fie sub un unghi de 120 °. Aceste puncte din triunghi sunt "asociate". Uneori aceste puncte se numesc puncte Fermat sau puncte Fermat-Torricelli.
- Două puncte Torricelli sunt puncte de intersecție:
- cu vârfurile libere corespunzătoare ale triunghiurilor echilaterale. construit pe laturile triunghiului (spre exterior) - primul punct al lui Torricelli
- cu vârfurile libere corespunzătoare ale triunghiurilor regulate construite în interiorul triunghiului - al doilea punct Torricelli.
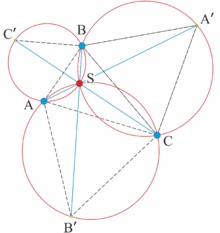
Construcția punctului Torricelli pentru triunghiuri cu unghiuri care nu depășesc 120 °.
Citat din Fermat: "Datis Tribus punctis, quartum reperire, a quo si ducantur tres rectæ de anunțuri de date puncta, Summa Trium Harum rectarum stau quantitas minimelor". P. de Fermat, «oeuvres de Fermat», 1679, Livre I, Paris. (Lat. „Pentru cele trei puncte având în vedere pentru a găsi a patra, astfel încât în cazul în care acesta să dețină o linie dreaptă la punctele de date, suma distanțelor este cea mai mică“ Fermat. ).
- Primul punct Torricelli are cea mai mică sumă de distanțe față de vârfurile triunghiului.
- Primul punct al lui Torricelli este punctul unui triunghi. din care toate laturile sunt vizibile la un unghi de 120 °. Există numai în triunghiuri cu unghiuri mai mici de 120 °, mai mult decât atât, este unic și, prin urmare, coincide cu punctul Fermat.
- Primul punct Torricelli este un caz particular al punctului Fermat. existente în orice triunghi.
- Două puncte Torricelli și punctul lemoian se află pe o linie.
- Punctele Torricelli sunt conjugate în mod izogonal cu punctele din Apollonia
- Construim două linii, fiecare dintre care trece prin punctul Apollonius și punctul Torricelli, diferit de conjugatul isogonal la acesta. Astfel de linii se intersectează la punctul de intersecție al medianilor (în centroidul triunghiului).
- Teorema Leicester [1]. În oricare două puncte ale triunghiului versatil centrul Torricelli de nouă puncte, iar centrul cercului circumscris minciuna pe un cerc (circumferința Leicester).
Hyperbole Kiperta - a descris hiperbolă, trecând prin centroid și orthocenter. Când laturile triunghiului pentru a construi triunghiuri isoscele similare (spre exterior sau spre interior) și apoi se combină nodurile lor cu vârfuri opuse ale triunghiului inițial, trei astfel de linii se intersectează într-un punct care se află pe hiperbola Kipert. În special, în acest moment al hiperbola se află Torricelli și punctul Napoleon (intersecția punctul chevian conectarea vertexul cu centre construite pe laturile opuse ale triunghiuri drepte) [2].
Apropo, în prima cifră spre dreapta, centrele a trei triunghiuri echilaterale sunt ele însele vârful unui triunghi echilateral nou (Teorema lui Napoleon). În plus, AA '= BB' = CC '.