Procesele oscilatorii cu care trebuie să se întâlnească sunt subdivizate în periodice și neperiodice, în funcție de natura schimbării cu timpul măsurării cantităților fizice care caracterizează starea sistemului. Datorită originii sale, fluctuațiile sunt împărțite în liber și forțate.
Oscilațiile libere (corecte) sunt oscilațiile care apar în sistem ca urmare a unei singure deducții inițiale din starea de echilibru stabil. Cu oscilații libere, forțele (în cazul general al cauzei) acționează întotdeauna în sistem, încercând să readucă sistemul la o poziție de echilibru. (În cazul unei sarcini oscilante pe arc, forța de elasticitate a arcului este forța de întoarcere.)
Dacă sistemul nu dispune de forțe de frecare și de alte motive care împiedică vibrațiile libere, atunci nu există nici o pierdere a energiei mecanice, iar oscilațiile pot avea loc atâta timp cât se dorește cu o amplitudine constantă. Asemenea oscilații libere sunt numite neîntrerupte. Oscilațiile oscilante reprezintă un caz idealizat de oscilații. Oscilațiile libere ale sistemelor reale sunt întotdeauna atenuate. Amortizarea oscilațiilor se datorează în principal acțiunii forțelor de frecare din sistem. Anumite oscilații în sistemul real pot fi excitate de acțiunea unei forțe externe variabile asupra acestuia. În acest caz, oscilațiile sunt numite forțate.
Periodic numite oscilații, în care valorile tuturor cantităților fizice care se schimbă în timpul oscilației sunt repetate la intervale regulate. Cel mai mic interval de timp, după expirarea căruia valorile tuturor cantităților care caracterizează mișcarea vibrațională se repetă, se numește perioada oscilațiilor. În acest timp, spun ei, există o fluctuație.
Frecvența oscilațiilor periodice este numărul de oscilații per unitate de timp. Dacă în timp sistemul produce oscilații, atunci frecvența de oscilație este egală cu: Având în vedere că pentru o perioadă egală cu o perioadă are loc o oscilație, ajungem la o conexiune de frecvență cu o perioadă:
Frecvența este măsurată în Hertz (Hz). Pentru 1 Hz luați frecvența unui astfel de proces oscilator, în care o oscilație completă este efectuată într-o secundă (Hz = 1 / s).
Un caz special de oscilații periodice sunt oscilațiile armonice în care cantitatea fizică oscilantă (de exemplu, coordonatul sarcinii asupra arcului) variază în funcție de timp, conform legii cosinusului (sau sinusului):
unde valoarea egală cu cea mai mare valoare absolută a cantității oscilante se numește amplitudinea oscilațiilor. Expresia determină valoarea în orice moment și se numește faza de oscilație. La momentul inițial, faza este egală cu faza inițială.
Valoarea se numește frecvența ciclică a oscilației armonice.
Perioada funcției (1), așa cum este cunoscută din matematică, este
- aceasta va fi perioada fluctuațiilor. Pentru frecvența unei oscilații armonice, avem:
Observăm că funcția (1) este o soluție a ecuației diferențiale:
unde este a doua oară derivată a funcției.
;
și după înlocuirea în ecuația (2), se transformă în egalitatea corectă, după cum este necesar.
În matematică se demonstrează că funcția (1) este singura soluție a ecuației diferențiale (2). Astfel, dacă oscilația pentru o cantitate fizică oscilantă în orice moment ia relația (2). atunci oscilațiile sunt armonice și apar cu o perioadă
Valorile constantelor u sunt determinate, de regulă, de condițiile inițiale.
În lucrarea de laborator 2, veți investiga experimental oscilațiile libere ale pendulului de primăvară și matematică.
Pendulul de primăvară. METODA EXPERIMENTALĂ
Un pendul de primăvară este un corp suspendat de un arc. Lăsați greutatea greutății arcului să fie suspendată de un arc (figura 1)
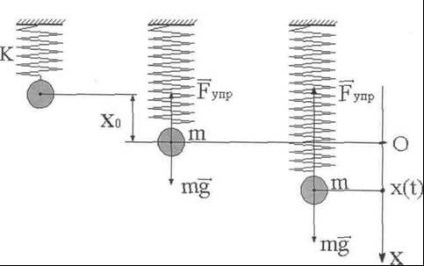
Luați în considerare mișcarea verticală a sarcinii, care va avea loc după o mică împingere sub forța elasticității arcului și forța gravitației. Primăvara este considerată a fi ușoară și masa sa neglijată. De asemenea, neglijăm forța rezistenței la aer, considerându-l ca fiind mic.
Cantitatea fizică oscilantă în acest exemplu este coordonatele sarcinii. Am plasat originea referinței de-a lungul axei până la punctul corespunzător poziției de echilibru a sarcinii (figura 1). În această poziție, arcul este deja întins cu o cantitate determinată din starea de echilibru
Atunci când sarcina este deplasată din poziția de echilibru, spre exemplu în jos, la o distanță, alta decât gravitația
Forța elastică acționează conform legii lui Hooke, așa cum se arată în figura 1.
Vom scrie ecuația celei de-a doua legi a lui Newton pentru sarcina în proiecție pe axă:
Luând în considerare relația (3), ecuația celei de-a doua legi a lui Newton este redusă la forma
unde proiecția accelerației pe axă nu este nimic asemănător cu al doilea derivat al coordonatelor de marfă, adică . Astfel, constatăm că într-o moment arbitrar de timp, când sarcina oscilează, coordonatele ei iau următoarea relație
În consecință, oscilațiile considerate sunt armonice și apar la o frecvență ciclică
În timpul experimentului, trebuie să vă asigurați că perioada nu depinde de amplitudinea vibrațiilor încărcăturii și de perioada de oscilație măsurată și de valoarea cunoscută a masei de sarcină, calculați rigiditatea arcului în conformitate cu relația (5)
Determinați rigiditatea arcului poate fi o altă metodă. Pentru aceasta, este necesar să se măsoare deformarea arcului în poziția de echilibru a ecuației de încărcare și de utilizare (3), conform căreia
După estimarea erorilor, valorile obținute trebuie comparate între ele și explică, dacă este necesar, motivele posibilei inconsecvențe.