Scopul lucrării. Să se familiarizeze cu principalele caracteristici ale vibrațiilor mecanice libere și neconfirmate.
Sarcina. Determinați perioada oscilațiilor naturale ale pendulului de primăvară; verificați liniaritatea pătratului perioadei față de masă; determină rigiditatea arcului; determină perioada de oscilații amortizate și scăderea logaritmică a amortizării pendulului de primăvară.
Aparate și accesorii. Un trepied cu o scară, un izvor, un set de încărcături de diferite mase, un vas cu apă, un cronometru.
1. Oscilații libere ale unui pendul de primăvară. Informații generale
Oscilațiile sunt procese în care una sau mai multe cantități fizice care descriu aceste procese se schimbă periodic. Oscilațiile pot fi descrise prin diferite funcții periodice ale timpului. Cele mai simple variații sunt oscilații armonice - aceste oscilații, în care fluctuante valoare (de exemplu, sarcina de compensare pe resortul) variază în funcție de timp, conform unui sinus sau cosinus. Oscilațiile care apar după acțiunea asupra sistemului unei forțe externe pe termen scurt sunt numite libere.
Luați în considerare unul dintre cele mai simple sisteme oscilatorii - un pendul de primăvară, care este o masă de masă m. suspendat pe un arc absolut elastic cu un coeficient de rigiditate k
(Figura 1). Fie l 0 lungimea arcului fără încărcare suspendată. Când suspendarea încărcăturii de arc gravitațional este întinsă la x 1, astfel încât pendulul va fi în echilibru datorită egalității mg module de gravitație și forța elastică F Ex: mg = kx 1, care tind să se întoarcă sarcina la poziția de echilibru (presupunând că deformarea arcului perfect elastice și să respecte legea lui Hooke).
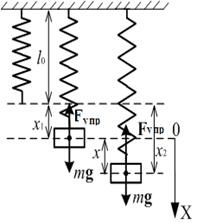
Dacă sarcina este retrasă din poziția de echilibru, prin deflectarea x. atunci forța de elasticitate crește: F упрпр = - kx 2 = -k (x 1 + x). După atingerea poziției de echilibru, sarcina va avea o viteză nenuloasă, iar poziția de echilibru va trece prin inerție. Pe măsură ce mișcarea continuă, abaterea de la poziția de echilibru va crește, ceea ce va duce la o creștere a forței elastice, iar procesul va fi repetat în direcția opusă. Astfel, mișcarea oscilantă a sistemului se datorează două motive: 1) dorința corpului de a reveni la poziția de echilibru și 2) inerția care nu permite corpului să se oprească imediat la poziția de echilibru. În absența forțelor de frecare, oscilațiile vor continua pe termen nelimitat. Prezența unei forțe de frecare conduce la faptul că o parte din energia vibrațiilor trece în energia internă, iar oscilațiile se descompun treptat. Astfel de oscilații sunt numite amortizate.
Oscilații libere oscilante
În primul rând, să luăm în considerare oscilațiile unui pendul de primăvară, pe care forțele de fricțiune nu acționează - oscilațiile libere neîntrerupte. Conform celei de-a doua legi a lui Newton, luând în considerare semnele proiecțiilor pe axa X.
Din starea de echilibru, deplasarea cauzată de gravitate :. Înlocuindu-ne în ecuația (1), obținem :. Împărțind laturile din dreapta și din stânga ale acestei ecuații cu m și presupunând că a = d2x / dt2. obținem ecuația diferențială
Această ecuație se numește ecuația diferențială a oscilațiilor armonice ale unui pendul de primăvară. Din această ecuație rezultă că după încetarea acțiunii externe care conduce la abaterea inițială a sistemului din poziția de echilibru, mișcarea sarcinii se datorează numai acțiunii forței elastice (gravitatea determină o deplasare constantă).
Soluția generală a unei ecuații diferențiale omogene de ordinul doi (2) are forma
Această ecuație se numește ecuația de oscilație armonică. Cea mai mare abatere a sarcinii din poziția de echilibru A 0 se numește amplitudinea oscilațiilor. Cantitatea din argumentul cosinusului se numește faza oscilației. constant 0 reprezintă valoarea fazei la momentul momentului inițial (t = 0) și se numește faza inițială a oscilațiilor. valoare
există o frecvență circulară sau ciclică a oscilațiilor naturale. legat de perioada de oscilație T de relație. Se determină perioada de oscilație
Să considerăm oscilațiile libere ale unui pendul de primăvară în prezența unei forțe de frecare (oscilații amortizate). În cazul cel mai simplu și cel mai frecvent întâlnit, forța de frecare este proporțională cu viteza # 965; circulație:
unde r este o constantă, numită coeficientul de rezistență. Semnul minus arată că forța și viteza de frecare au direcții opuse. Ecuația celei de-a doua legi a lui Newton în proiecția pe axa X cu prezența forței elastice și a forței de frecare
Această ecuație diferențială cu alocația pentru # 965; = dx / dt poate fi scris
unde este coeficientul de atenuare; Este frecvența ciclică a oscilațiilor libere neambalate ale unui sistem oscilator dat, adică în absența pierderilor de energie (# 946; = 0). Ecuația (8) este numită ecuația diferențială a oscilațiilor amortizate.
Pentru a obține dependența deplasării x pe timpul t. este necesară rezolvarea ecuației diferențiale (8). În cazul amortizării mici (), soluția ecuației poate fi scrisă după cum urmează:
unde A 0 și - amplitudinea inițială și faza inițială a oscilațiilor;
- frecvența ciclică a oscilațiilor amortizate la # 969; >> # 969; ≈ # 969;
Mișcarea încărcăturii în acest caz poate fi considerată o oscilare armonică cu frecvență # 969; și amplitudine variabilă, variind în conformitate cu legea:
Pe graficul funcției (9), Fig. 2, liniile punctate arată modificarea amplitudinii (10) a oscilațiilor amortizate.
Fig. 2. Dependența deplasării x a sarcinii la timpul t în prezența unei forțe de frecare
Pentru caracterizarea cantitativ gradul de amortizare a trepidațiilor cantității relative introduse amplitudini egale care diferă în perioada și numitul factor de amortizare:
Logaritmul natural al acestei cantități este adesea folosit. Un astfel de parametru se numește decrementarea logaritmică a amortizării:
Dacă amplitudinea scade cu un factor de n în timpul t ', atunci rezultă din ecuația (10) că
Prin urmare, pentru decrementul logaritmic obținem expresia
Dacă amplitudinea scade cu un factor e în timp t '(e = 2,71 este baza logaritmului natural), atunci sistemul va avea timp să facă numărul de oscilații
În consecință, logaritmică decrementare - inversul numărului de oscilații efectuate pentru intervalul de timp în care amplitudinea este redusă cu un factor e. Mai mult # 952; cu cât oscilația se descompune mai rapid.
2. Procedura experimentală și configurarea experimentală
Fig. 3. Diagrama de instalare
Instalația constă dintr-un trepied 1 cu o scară de măsurare 2. La trepiedul de pe arcul 3 se încarcă încărcături de 4 mase diferite. Când se studiază oscilațiile amortizate în sarcina 2, pentru a spori amortizarea, se utilizează inelul 5, care este plasat într-un vas transparent 6 cu apă.
În sarcina 1 (efectuată fără un vas cu apă și un inel), în prima aproximare, atenuarea oscilațiilor poate fi neglijată și considerată armonică. După cum rezultă din formula (5) pentru oscilațiile armonice, dependența T 2 = f (m) este liniară, din care este posibil să se determine coeficientul de rigiditate al arcului k prin formula
unde este panta liniei drepte T 2 de la m.
Sarcina 1. Determinarea dependenței perioadei de oscilații naturale a pendulului de primăvară de masa încărcăturii.
1. Pentru a determina perioada de oscilație a arcului pendulului la diferite valori ale masa m sarcină. Pentru a face acest lucru cu un cronometru pentru fiecare valoare de m timp t măsurată de trei ori complet n oscilație (n ≥10) și perioada de timp valoarea medie calculată. Rezultatele sunt prezentate în Tabelul. 1.
2. Din rezultatele măsurătorii, competați un grafic al pătrații perioadei T2 pe masa m. Din coeficientul unghiular al graficului, determinați rigiditatea arcului k prin formula (16).
Rezultatele măsurătorilor pentru determinarea perioadei de oscilații naturale
3. Sarcina suplimentară. Estimați aleatoriu, complet și relativ # Erorile de măsurare a timpului pentru valoarea m = 400 g.
Sarcina 2. Determinarea decrementării decrementării logaritmice a unui pendul de primăvară.
1. Primăvara atârnă o sarcină de 400 g m = un inel și plasat într-un recipient de apă, astfel încât inelul este în întregime în apă. Se determină perioada de oscilație amortizată pentru o valoare dată m prin metoda descrisă în Sec. Un loc de muncă 1. Măsurători repetate de trei ori și rezultatele înregistrate în partea stângă a tabelului. 2.
2. Trageți pendulul din poziția de echilibru și, marcând amplitudinea sa inițială de-a lungul riglei, măsurați timpul t '. în care amplitudinea oscilațiilor scade cu un factor de 2. Măsurați de trei ori. Rezultatele sunt introduse în partea dreaptă a tabelului. 2.
3. Calculați prin formula (14) scăderea logaritmică a atenuării # 952; luând în considerare faptul că ln2 = 0,693.
pentru a determina scăderea logaritmică a atenuării
Măsurarea perioadei de oscilație
amplitudinea scade cu 2 ori
4. Testați întrebările și sarcinile
1. Ce oscilații se numesc armonici? Oferiți o definiție a caracteristicilor lor principale.
2. Ce oscilații se numesc decolorări? Oferiți o definiție a caracteristicilor lor principale.
3. Explicați semnificația fizică a reducerii logaritmice a decrementului și a coeficientului de atenuare.
4. Derulați dependența de timpul de viteză și de accelerația sarcinii pe un arc care efectuează oscilații armonice. Aduceți diagramele și analizați-le.
5. Determinați dependențele de timpul de energie cinetică, potențială și totală a sarcinii, oscilând pe arc. Aduceți diagramele și analizați-le.
6. Obțineți o ecuație diferențială de oscilații libere și soluția sa.
7. Construiți grafice ale oscilațiilor armonice cu fazele inițiale π / 2 și π / 3.
8. În ce măsură se poate schimba diminuarea logaritmică a amortizării?
9. Dați ecuația diferențială a oscilațiilor amortizate ale unui pendul de primăvară și ale soluției sale.
10. Prin ce lege se modifică amplitudinea oscilațiilor amortizate? Sunt periodic oscilațiile amortizate?
11. Ce mișcare se numește aperiodică? În ce condiții este observat?
12. Care este frecvența de oscilație naturală? Cum depinde de masa corpului oscilant pentru un pendul de primăvară?
13. De ce frecvența oscilațiilor amortizate este mai mică decât frecvența oscilațiilor naturale ale sistemului?
14. Suspendat la un resort, o bilă de cupru face vibrații verticale. Cum se va schimba perioada de oscilație dacă o suspensie de aluminiu este plasată în aceeași rază în locul unei mingi de cupru?
15. La ce valoare a decrementării decrementării logaritmice, oscilațiile se diminuează mai rapid: când # 952; 1 = 0,25 sau # 952; 2 = 0,5; Dați grafice ale acestor oscilații amortizate.
Laboratorul Un curs practic în fizică.
- M. Engleză. săpt. 1980. - 359 p.