Conversia unui întreg la un șir folosind o stivă (lst_recstack)
De fiecare data cand toStr. pe teanc este plasat un simbol. Revenind la exemplul anterior, putem vedea că după al patrulea apel laStr stiva va arăta ca în figura 5. Rețineți: acum putem pur și simplu să împingem simbolurile din stivă și să le îmbinăm în rezultatul final "1010".
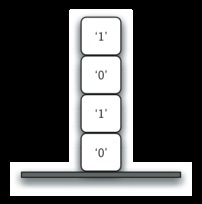
Figura 5: Șiruri plasate pe teanc în timpul conversiei.
Exemplul precedent ne dă o idee despre modul în care Python a implementat apeluri recursive. Când apelați o funcție pentru a controla variabilele sale locale, cadrul stivei este evidențiat. Valoarea returnată la sfârșitul funcției va fi în partea de sus a stivei, accesibilă părții de apel a programului. Figura 6 ilustrează stiva după declarația de returnare din rândul 4.
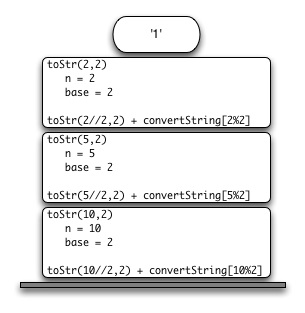
Figura 6: Stivă apeluri generate laStr (10, 2).
Rețineți că apelul cătreStr (2 // 2, 2) părăsește valoarea de returnare a stivei "1". Apoi se înlocuiește funcția toStr (1, 2) în expresia "1" + convertString [2% 2]. care iese din partea de sus a stivei "10". Astfel, stiva de apeluri Python funcționează la fel ca stiva, pe care am folosit-o explicit în Lista 4. În exemplul nostru de însumare, vă puteți gândi la valoarea de întoarcere a stivei ca o variabilă acumulatoare.
De asemenea, cadrul stivei oferă un domeniu pentru variabilele utilizate de funcție. În ciuda faptului că numim în mod repetat aceeași funcție, fiecare apel creează un domeniu de aplicare pentru variabilele sale locale.
Dacă înțelegeți bine ideea stiva, atunci va fi mult mai ușor să scrieți funcțiile recursive corespunzătoare.