1. Scopul muncii
Determinarea lățimii benzii interzise a unui semiconductor de-a lungul marginii absorbției intrinseci și din spectrul de electroluminescență.
2. Bazele teoretice ale muncii.
Interacțiunile dintre electroni și miezul de ioni din cristal nu pot distruge complet structura nivelurilor de electroni ale atomului. Aceste interacțiuni provoacă perturbații notabile ale nivelurilor de energie ale cojilor exteriori (valenți) ai atomilor liberi. Cea mai importantă consecință a acestor perturbații este împărțirea nivelelor discrete de energie a electronilor de valență în benzile cvasi-continue de bandă-energie.
Un calcul riguros al spectrului energetic al electronilor dintr-un solid sugerează soluția ecuației Schrödinger pentru o latură cristalină. Dacă luăm în considerare faptul că într-un centimetru cub de corp solid există aproximativ 10-23 de atomi, devine evident că o soluție riguroasă a unei astfel de probleme este imposibilă, chiar și cu ajutorul celor mai sofisticate computere.
Pentru o descriere calitativă a împărțirii nivelurilor de energie, să luăm în considerare un exemplu clasic - două pendulumuri de primăvară (interacționează) (Figura 55.1). Dacă nu există nici o interacțiune (nu există niciun resort intermediar), atunci frecvența de oscilație naturală a fiecărui pendul este ω0 = (x / m) 1/2. unde x este rigiditatea jetului și m este masa mingii. Când bilele interacționează prin arcul mijlociu, forța elastică care acționează asupra bilei depinde de deformările celor două arcuri. Ecuația diferențială pentru fiecare minge va include un termen suplimentar care caracterizează poziția celeilalte minge. Din soluția acestor ecuații rezultă că orice oscilații ale așa-numitului sistem "cuplat" sunt rezultatul adăugării a două oscilații armonice cu frecvențele naturale ωa și ωc cu ωa> ωο> ωc. Aici ωa este frecvența antifazei și ωσ este frecvența oscilațiilor în fază. Deci, două sisteme identice cu aceleași frecvențe eigen. Diferența ωa - ωc este cea mai mare, cu atât interacțiunea este mai puternică.
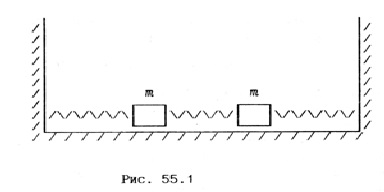
Dacă folosim formula lui Planck pentru cuantumul energiei, atunci din argumentele de mai sus rezultă că a avut loc împărțirea în două niveluri de energie (amintim că energia cuantică este e = ħω). O astfel de divizare a nivelurilor de energie apare în cristale. Luați în considerare schema unui "cristal liniar" format dintr-un lanț de noduri de cristal (Figura 55.2). Ca cel mai simplu metal, alegem litiu (Z = 3). Litiul are trei electroni, dintre care doi (conform principiului Pauli) sunt în starea 1s, iar al treilea este în starea 2s. În Fig. 55.2 axa x este reprezentată grafic de-a lungul absciselor; Poziția nodurilor rețelei cristaline este determinată de constanta cristalină a. Ordonata arata energia potentiala a electronilor din cristal. Liniile solide arată energia potențială a electronilor într-un cristal - rezultatul însumării energiei câmpului potențial al fiecărui nod de cristal. Energia potențială a unui electron în câmpul unui atom izolat este prezentată în acest grafic într-o linie întreruptă. Din fig. 55.2 că interacțiunea are loc între electroni (în special electroni periferici, valenți). Acești electroni se pot deplasa în jurul cristalului, nu mai au același nod. Ei spun că electronii sunt colectivizați.
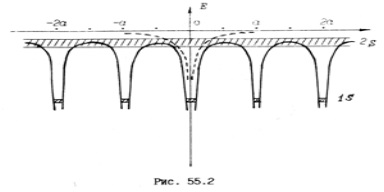
Ca urmare a interacțiunii, nivelurile de energie ale electronilor sunt împărțite. Aceasta poate fi interpretată ca o consecință a principiului Pauli: într-un sistem cuantic, nici doi electroni nu pot avea aceleași valori ale tuturor celor patru numere cuantice. Amploarea divizării (ca în cazul bilelor) nu depinde de numărul de atomi din cristal, ci numai de gradul de interacțiune dintre ele. În Fig. 55.3 prezintă schematic divizarea nivelelor 1s și 2s cu abordarea treptată a "lanțului" de șase atomi de litiu. Distanța R0 corespunde distanței dintre siturile zăbrele într-un cristal real. Fiecare nivel de energie se împarte în N = 6 sublevels, lățimea de despicare crește cu scăderea R. De obicei, lățimea benzii permise pentru electronii periferici este de 1,3 eV.
Notă. În continuare, noțiunile de "lățime a zonei", "distanță între zone" și altele asemenea. sunt intelese in sensul ca acestea sunt diferentele energetice pe axa E (energia este in mod traditional indicata prin litera E din sectiunea fizica a fizicii Solid State).
Pentru litiu, lățimea așa-numitei zone rezolvate 2s este 1. 3 eV, lățimea benzii 1s pentru litiu este
0,01 eV. 1 cm3 conține N
10-23 de atomi, astfel încât distanța dintre subsoluri în zona energiilor permise este de ordinul 10-22 eV. Reamintim că energia medie a mișcării termice la T = 300 K este de ordinul kT. Aici k este constanta Boltzmann, iar T este temperatura pe scara Kelvin. Astfel, valoarea energiei medii a mișcării termice kT-10 -21 eV este mult mai mare decât distanța dintre subsolurile din zona permisă.
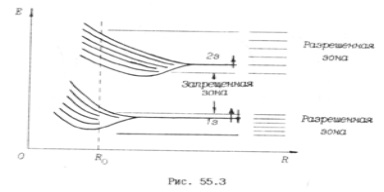
Din cele de mai sus rezultă că banda de energie permise poate fi privită ca fiind cvasi-continuă. Cu toate acestea, numărul de stări și, în consecință, numărul de electroni din zonă este finit: pentru zona 2s, pentru care numerele cuantice n, I și m sunt fixe (n = 2, I = 0, m = 0) nodurile rețelei cristaline. Coeficientul 2 reflectă două orientări posibile ale rotației electronilor.
Pentru a ilustra dependența lățimii benzii permise de gradul de interacțiune din Fig. Figura 55.2 prezintă zone schematice permise 1s și 2s pentru un cristal de litiu. Interacțiunea dintre electroni în starea 2s este mult mai mare decât între electronii în starea 1s, astfel încât lățimea benzii 2s este mult mai mare.
Zonele permise sunt separate prin intervale care nu conțin niveluri de energie permise. Aceste intervale sunt numite zone interzise. Existența benzilor interzise este o consecință a proprietăților undelor electronilor.
Trebuie subliniat faptul că formarea zonelor din nivele atomice are loc în toate tipurile de cristale. Diferența dintre corpurile solide (prin conductivitate electrică, conductivitate termică și alte proprietăți fizice) este o consecință a aranjamentului reciproc al zonelor și a umplerii acestora.
De exemplu, să luăm din nou în considerare cel mai simplu metal-litiu. Există trei electroni în atomul de litiu: doi dintre ei sunt în starea 1s, unul este în starea 2s. În Fig. 55.3 săgețile arată direcțiile rotirilor electronilor. Zona 1s, care are posturi vacante 2N, este complet umplută, zona 2s este pe jumătate goală. Există nivele de energie neocupate în ea. Este suficient să se informeze electronul unei astfel de zone de energie de ordinul 10-22 eV, astfel încât să se transfere la un nivel adiacent, adică își schimbă impulsul și energia. La temperatura camerei într-un câmp electric cu intensitate
10 5 V / m pentru o traiectorie medie liberă egală cu distanța dintre locurile de zăbrele a
10-10 m într-o zonă ne-umplută, electronii pot trece de la un nivel de energie la altul, adică accelerați de un câmp electric. Rezultă că conductorul de litiu. Zona parțial umplută a conductorului se numește banda de conducție.
Să luăm în considerare cazurile prezentate în Fig. 55,4. În stânga și în dreapta axei energetice sunt reprezentate zonele de energie sub formă de dreptunghiuri. Între dreptunghiuri - zonele cu energie interzisă. În jumătatea stângă a Fig. 55.4 două zone inferioare permise sunt umbrite. Aceasta înseamnă că sunt complet umplute. Electronii din aceste zone (la niveluri de energie adecvate) nu pot lua parte la conductivitatea electrică. Următoarea zonă este umbrită la jumătate. Aceasta înseamnă că este parțial umplut. Chiar și un câmp electric foarte slab poate transfera electroni în această zonă de la un subsol la altul. În acest caz, electronii care se deplasează împotriva câmpului sunt accelerați, electronii care se mișcă în direcția câmpului vor încetini. Un curent electric apare în cristal. Această zonă este banda de conducție, cristalul conductorului corespunzător.
Din jumătatea dreaptă a Fig. Figura 55.4 prezintă un cristal în care cele trei zone inferioare sunt complet umplute cu electroni (acestea sunt umbrite). Banda superioară umplută corespunde stărilor electronilor de valență. Se numește banda de valență. Nu există electroni în zona necompletată superioară (se numește banda de conducere). Electronii din banda de valență nu pot participa la conductivitatea electrică (principiul Pauli nu permite ca electronul să treacă la un nivel de energie deja ocupat, dar nu există nivele neocupate în zonă). Un astfel de cristal este fie un izolator, fie un semiconductor.
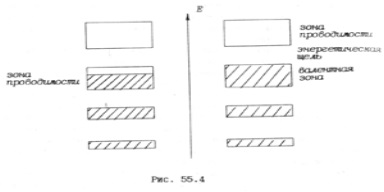
Între banda de valență și banda de conducere există o bandă interzisă - regiunea energetică dintre nivelul superior al benzii de valență și nivelul inferior al benzii de conducere. Cristalul nu poate conține electroni cu energii care corespund acestui interval de energie. Prin urmare, o zonă interzisă este denumită uneori un gol energetic. De obicei, intervalul său este notat cu simbolul Eg (din cuvântul "gap gap").
Dacă există o bandă interzisă, tranzițiile de electroni între banda de valență și banda de conducție sunt posibile numai în prezența unei surse de energie externe capabile să furnizeze suficientă energie pentru electron. Lățimea intervalului de bandă este un criteriu care ne permite să clasificăm un cristal ca o clasă de semiconductori sau o clasă de dielectrici (izolatori). Cristale în care lățimea intervalului de bandă Eg> 2 eV se numește dielectric, iar cristalele pentru care Eg<2 эВ - полупроводниками. Так, алмаз (Еg=1эВ ) - хороший изолятор, а кремний (Eg= 1,09 эВ) и гер-маний (Eg= 0,72 эВ) - полупроводники.