2. Expunerea conceptuală a problemei
2.1. Elemente geometrice ale rampelor de lansare
sare mica 20-45 m
jumătatea medie 50-70 m
traversă normală 75-90 m
platforme mari de 105-120 m
traversă pentru zborurile 145-185 m
Competițiile în Rusia se desfășoară, de regulă, pe salturi mari și competiții internaționale - pe trambuline pentru zboruri. Pentru a se asigura că schiorul care se duce la înregistrare nu se rupe, zburând pe panta debarcării sau cu puțin timp înainte, există formule și norme speciale pentru calcularea parametrilor geometrici ai săriturilor.
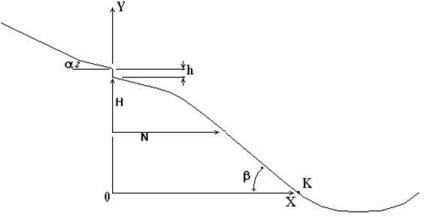
Fig. 1. Elemente geometrice de bază ale traverselor
Trapa este alcătuită dintr-un spațiu pentru dispersare și așa-numita masă de detașare, de unde schiorii părăsesc zborul liber. Masa de rupere este înclinată la orizontală la un unghi negru ușor, de obicei între -6 ° și -12 °. Aici se termină rampa de tracțiune reală și tot ceea ce urmează este numit un munte de adâncime sau un munte de trambulină. Înălțimea mesei de detașare de deasupra dealului de aterizare este de obicei indicată și variază de la 2% la 4% din intervalul maxim indicat. Rampă de montare este format din trei secțiuni: lungimea pantei parcela netratată și o lățime, porțiunea de aterizare - panta porțiunii drepte care constituie un unghi negativ față de orizontală este egală în conformitate cu standardele acceptate de la -25O la 40o, iar porțiunea de frânare. Zona de frânare are, de regulă, un profil, rotunjită fără probleme. Distanța orizontală de la marginea detașării - punctul final al mesei de detașare - este indicată până la punctul de distanță maximă. Această literă indică, de asemenea, punctul critic - sfârșitul zonei de aterizare.
2.2. De fapt, setarea conceptuală
Pe scurt, scopul acestei lucrări este: "cum să săriți pentru a zbura și a nu rupe?" Schimbând poziția sa în timpul detașării, poziția relativă a picioarelor, a brațelor și a corpului, atletul poate controla traiectoria zborului său în aer, controlând unghiul de atac. Sarcina este formulată după cum urmează: cum ar trebui să conducă schiorul corpul său să aterizeze pe cât posibil, în timp ce încă mai are o viteză acceptabilă de aterizare.
Dacă începutul și zborul sunt normale, este aproape imposibil să aterizați înainte de începerea pantei de aterizare. Dar există un alt pericol. Schiorul încheie zborul cu o viteză mare, care trebuie să fie stinsă. Pentru aceasta, există o porțiune ușor rotunjită a frânării. Dar dacă jumper-ul zboară punct critic, acesta este un risc grav, atunci rotunjit panta, iar unghiul de calea potrivită pentru panta, nu va mai fi 5-10O, și multe altele. Prin urmare, aterizarea mai mult decât sau mai târziu decât cea special creată pentru acest loc de aterizare în primul caz este imposibilă, iar în al doilea - este inacceptabilă. Partea paralelă a vitezei este stinsă, cu deplasarea în continuare a schiorului pe o pantă rotunjită. Cel mai mare pericol în aterizare este o componentă de viteză perpendicular pe pantă, deoarece la prea mare viteză normală în adiție sarcinile de impact de mare, există riscul, de asemenea, se încadrează - în acel moment, în viteza de aterizare a schiorului are câteva zeci de km / h. Prin urmare, componenta normală a vitezei de aterizare nu trebuie să depășească 7 m / s și de preferință să fie de 3-5 m / s.
3. Formularea matematică a problemei
Axa abscisă este îndreptată spre zborul schiorilor paralel cu orizontul, axa y se ridică prin marginea mesei de separare, numită marginea detașării. Originea este localizată astfel încât abscisa punctului de plecare și ordonata punctului critic - sfârșitul locului de aterizare - sunt zero. Dacă nu există vânt lateral și alte perturbații, centrul de masă al schiorului descrie curba în plan vertical, adică problema de zbor poate fi considerată ca fiind una bidimensională.
Evident, un jumper poate schimba parametrii aerodinamici, care sunt influențați de următorii factori:
momentul cinetic al sistemului de schiuri în raport cu axa perpendiculară pe planul figurinei și care trece prin centrul de masă al sistemului, în momentul detașării și în zbor;
Modificați momentul inerției sistemului în raport cu aceeași axă în timpul zborului;
diferite efecte active și reactive asociate cu rotația diferitelor părți ale corpului datorită muncii mușchilor.
Rezultatele multor studii ale telegramelor [1, 5] demonstrează poziția statică relativă a fiecărui jumper în timpul zborului. Aceasta simplifică descrierea modelului de deplasări și viteze ale sistemului de schi-schi și permite utilizarea caracteristicilor experimentale individuale obținute în tunelul aerodinamic. Din acest motiv, se presupune că invariabilitatea posturii de zbor a zborului a fost făcută.
Întregul salt poate fi împărțit în patru faze: decolare, grupare, zbor efectiv și pregătire pentru aterizare. Prima fază durează aproximativ 0,3 s, cea de-a doua - 0,8-0,9 s, a treia - 0,3-0,6 s. Toată restul poziției schiorului practic nu se schimbă - vezi figura 2 [1].
Fig. 2. Modificarea unghiului de atac al unui jumper în timpul unui salt
(pe axa abscisa, raportul dintre intervalul curent si intregul interval al saltului este reprezentat grafic, de-a lungul axei ordonate este unghiul de atac al trunchiului in grade conform rezultatelor saltului mediu).
Astfel, în faza principală, zborul jumperului este aproape de mișcarea de translație, ceea ce face ca naturale să înlocuiască luarea în considerare a jumper-ului prin luarea în considerare a mișcării centrului său de masă.
Informații despre lucrarea "Modelarea matematică a zborului unui schior în timpul unui salt de la o rampă de lansare"
Sectiunea: Matematica
Numărul de caractere cu spații: 31890
Număr de mese: 0
Număr imagini: 18