Capitolul V. Metoda coordonatelor în spațiu. § 1. Coordonatele punctului și coordonatele vectorului. → numărul 406
Să luăm în considerare cazul general. Luați în considerare doi vectori non-coplanari AB și DC. Transferăm vectorul DC în paralel astfel încât punctul D1 al originii să coincidă cu punctul B al capătului primului vector. Obținem vectorul D1C1 sau, care este același, vectorul BC1 este co-direcțional cu vectorul DC și egal cu el pe lungime. Conform regulii de adăugare a vectorilor:
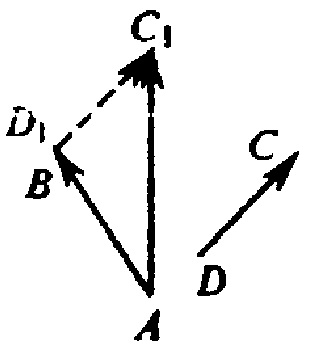
Pentru dovada exprimăm coordonatele acestor vectori în ceea ce privește coordonatele
Începutul și sfârșitul lor.
Din denumirile coordonatelor vectorului AB ca x1, y1 și z1 și vectorul BC1 ca x2, y2, z2, obținem
Sumele coordonatelor x1 + x2, y1 + y2, z1 + z2 sunt coordonatele vectorului AC1 egale cu suma vectorilor originali AB și DC. După cum este necesar pentru a dovedi.
← 407. Având în vedere vectorii a, b, c și d<— 2,7; 3,1; 0,5>. Găsiți coordonatele vectorilor: a) a + b; b) a + c; c) b + c; d) d + b; e) d + a; e) a + b + c; g) b + a + d; h) a + b + c + d