
O nouă carte despre genealogia ADN arată imaginea mutațiilor din cromozomul Y al strămoșilor străvechi umani de sute de mii de ani și arată conexiunea acestei imagini a mutațiilor cu istoria omenirii. Se arată cum aceste imagini ale mutațiilor pot fi transformate în indicatori cronologici și până în prezent evenimente istorice antice și relativ recente în anii, secolele, mileniile. În acest caz, cronometrul care permite dating nu este "extern", ci este integrat în ADN-ul nostru. Prin urmare, calculele din genealogia ADN sunt protejate fundamental de manipulările "din afară", cum ar fi, de exemplu, perioadele de semi-transformări ale elementelor radioactive în fizică și chimie sunt protejate. Indiferent ce trebuie făcut, și decăderea radioactivă "se bate" în timp, așa cum se presupune prin legile fizice. Același lucru în genealogia ADN - mutații "bifați" în conformitate cu aceleași legi, principiile de principiu sunt aceleași. Aceste legi reprezintă baza metodologică a genealogiei ADN-ului, iar această fundație ne permite să construim istoria dezvoltării omenirii pe toate continentele.
Deci, cartea arată genealogiei ADN în haplogrupuri de la A la T. Cu alte cuvinte, descrie un ADN-Genealogie fiecare cititor-bărbați, fără excepție, care aproape literal, unul - de la înălțimea de „zbor de pasăre“, și că a fost literală - trebuie doar să faceți un test pentru haplogroups-sublocuiri și haplotipuri. Pentru cine această carte? Pentru cei care doresc să înțeleagă istoria propriei lor și strămoșii lor, și modul în care istoria personală este încorporat în istoria grupului lor etnic, țară, toată omenirea.
Cartea: Genealogia ADN-ului de la A la T
Cum se calculează erorile din genealogia ADN?
Cum se calculează erorile din genealogia ADN?
RELATIVE EROARE TOTAL - o valoare importantă ce indică intervalul de încredere, sau pentru a determina distanța până la fiabilitatea duratei de viață a strămoșul comun al populației în cauză. În conformitate cu regulile statisticii matematice, calcul de eroare este de obicei făcută pentru „sigma“ sau „două sigma“, ceea ce corespunde la 68% și, respectiv, intervalul de încredere de 95%. Pentru sigma ia inversul rădăcinii pătrate a numărului total de mutații în seria haplotipuri, este pătrat, adăugat la acesta 0,01 (un pătrat valoarea medie eroare a ratei de mutație constantă atunci când a primit o eroare de ± 10%, adică 0,1), și din care rezultă rădăcina pătrată este extrasă.
De exemplu, cu 100 de mutații (de la haplotipul de bază) într-o serie de haplotipuri, obținem:
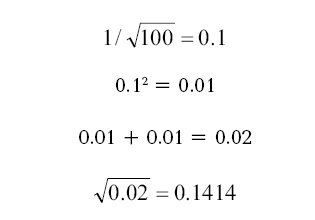
Astfel, eroarea de calcul pentru 100 de mutații din serie este de ± 14,14% sau, rotund, de 14%. Aceasta este pentru intervalul de încredere de 68% (un sigma).
Pentru intervalul de încredere de 95% (două sigma), valoarea obținută este dublată, adică eroarea de calcul este de ± 28%. Dar experiența arată că pentru calculul genealogiilor reale, documentate, intervalul de încredere al unui sigma este realist. Ideea este că cerința de precizie de 95% este nerealistă pentru serii limitate de haplotipuri. Mai mult decât atât, luând în considerare mai multe sute de pârtii experimentale haplotipuri a arătat că pune eroare pentru constantele de viteză mutații ± 10% este prea mare, în practică, nu depășește ± 2,5%. Prin urmare, cu 100 de mutații într-o serie de haplotipuri, eroarea la un sigma nu este ± 14,14%, dar ± 10,31%.
Erori sunt calculate prin aceleași reguli pentru numărul de mutații și pentru ratele de mutație în markerii individuali și în haplotipuri care conțin orice număr de markeri. De exemplu, în markerul DYS391, se observă 59 de mutații pentru o serie de 275 haplogroups de haplopete N1c1. Conform regulilor statistice pentru un sigma, aceste 59 de mutații corespund efectiv la 59 ± 8 mutații, astfel încât incertitudinea sau eroarea începe deja aici. Eroarea este obținută ca reciprocitate a rădăcinii pătrate, convertită la o valoare de 13,02%. Dacă traduce acest număr de mutații în numărul mediu de mutații pe un marker, vom obține 59/275 = 0.2145, dar este recomandabil să se înregistreze eroarea la sfârșitul calculelor, în scopul de a simplifica calculul. Cu corecție pentru mutația recurente (vezi. Sidebar) că numărul mediu de mutații pe jeton este egal cu 0.2402, iar din moment ce valoarea constantelor de viteză de mutație pentru jeton DYS391 este egal cu 0,0022, vom vedea că „vârsta“ pentru marcatorul DYS391 pentru această serie de haplotipuri este 0.2402 / 0.0022 = 96 generații convenționale, sau 2400 de ani. Eroarea aici este deja mai mare decât cea de mai sus ± 13,02% deoarece adaugă o eroare în determinarea constantei ratei de mutație, care în acest caz nu este mai mică de ± 30%. Ca rezultat, reciproca rădăcina pătrată din 59 cvadratura (randament 0.01695) se adaugă 0,09 (erori la pătrat în determinarea constanta ratei de mutație), se extrage rădăcina pătrată din această sumă și constată că eroarea (care este, de asemenea, numită deviație standard) este egală cu acest caz este de ± 32,7%. Vedem că atunci când am introdus constantitatea ratei de mutație în calcule, eroarea a fost mai mult decât dublă. Obținem că indicatorul DYS391 din această serie indică faptul că "vârsta" eșantionului este de 2400 ± 800 ani.
Dar, în cazul în care calculul este efectuat pe toți marcatorii dintr-o dată, mai degrabă decât valorile individuale, numărul de alele și mutații în ele în mii, și care rezultă de eroare „vârsta“ este drastic redusă, dar niciodată nu devine mai mică decât eroarea în determinarea ratei de mutație constantă. Acesta din urmă este de obicei luat ca ± 10%, deși este cu siguranță mai mic decât această valoare, așa cum sa explicat mai sus.