Privind prin forum, am dat peste mesajul meu mai mult de 8 ani în urmă. În mesaj, am adresat publicului o întrebare care, în general, a fărâmat problema diferențierii matricei în raport cu un vector. La momentul redactării acestei note, nu am primit niciodată un răspuns. În același timp, acum nu văd nici o dificultate fundamentală în această sarcină.
Problema este frecventă pentru universitățile tehnice: în primul an vi se vorbește despre fenomene fizice, pentru descrierea cărora trebuie să înțelegeți rotorul. gradientului. divergență. și ce fel de operatori și cum să le folosească - se vor spune în al doilea an.
La prima vedere, nimic nu este clar: operatorul de diferențiere este aplicat matricelor, dintre care unele sunt de asemenea transpuse, diferențierea are loc pe un vector etc. Dar nu intră în panică: există reguli pentru calcularea derivatelor atât a urmei matricei, cât și a determinantului produsului matricelor sau a logaritmului determinant al matricei - în cazul nostru (forum) totul este destul de simplu.
În primul rând, descriem regulile generale de diferențiere atunci când lucrăm cu obiecte similare.
Derivatul unui vector în raport cu un scalar este un vector de aceeași dimensiune, constând din derivații elementelor corespondente
Derivatul funcției scalare f din argumentul vectorial x este un vector cu aceeași dimensiune ca x. egal
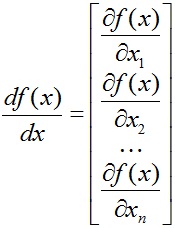
(Adică, un vector compus din derivate parțiale ale lui f de-a lungul elementelor vectorului x).
Derivatul unei funcții vectoriale g a dimensiunii m în raport cu un argument vector x al dimensiunii n este o matrice cu dimensiunea m x n. în care prima linie constă din derivații parțiali ai elementului g1 de către elementele vectorului x, etc.:
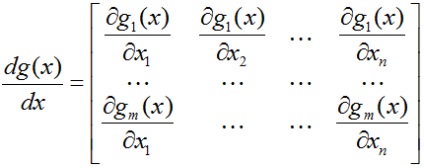
Următoarele două rezultate din algebra liniară pot fi obținute prin efectuarea cu atenție a diferențierii conform regulilor considerate anterior. Aceste formule sunt adesea folosite, așa că le vom scrie:
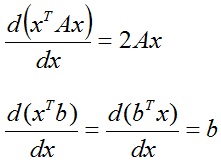
De fapt, revenirea la problema inițială (o întrebare pe forum):
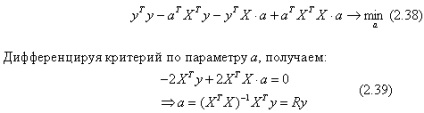
Cum putem diferenția (2.38) și obținem (2.39)?
Luați în considerare derivații sumelor din (2.38).
Pentru prima dată, totul este evident din înțelesul derivatului:
Al doilea termen (aici folosim una din formulele gata descrise mai devreme):
Al treilea termen (folosim aceeași formulă finită, dar în prealabil ușor "finalizează" expresia):
Dacă nu înțelegeți "transformarea" de mai sus - încă o dată:
Aici am folosit proprietățile de transpunere ale matricelor:
Transpunerea matricei este egală cu produsul matricelor transpuse, luate în ordine inversă.
[. ]
Matricea A transmisă de două ori este egală cu matricea originală A.
Cu ajutorul acestor proprietăți am realizat transformări care reduc expresia la o formă convenabilă pentru aplicarea formulării finite.
Al patrulea termen (folosim cealaltă formulă terminată):
Vom strânge împreună și vom grupa termenii:
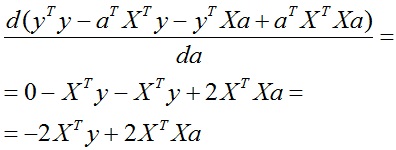
Acesta este rezultatul obținut în (2.39).