93. Papagalul a trăit mai puțin de 100 de ani și este capabil să răspundă doar la întrebările "da" și "nu". Câte întrebări ar trebui să le solicite pentru a-și cunoaște vârsta?
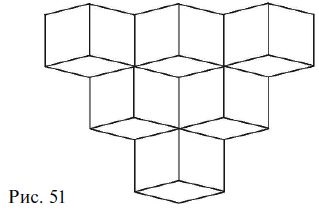
94. Câte cuburi sunt prezentate în Fig. 51?
95. Trei viței - câte picioare?
96. O persoană prinsă în captivitate, a declarat următoarele: „închisoarea mea a fost localizat în partea de sus a castelului Dupa zile de efort am fost în stare să rupă jos unul dintre barurile din fereastra îngustă în gaura ar putea obține prin intermediul, dar distanța până la sol a fost prea mare pentru a .. sari în jos. Într-un colț al închisorii am găsit o frânghie pe cineva uitat. cu toate acestea, ea a fost prea scurt pentru a putea merge în jos pe ea. apoi mi-am amintit, ca un intelept lungit prea scurt pentru el o pătură, taie o parte din ea din partea de jos și coase-l pe partea de sus . Așa că am grăbit să reducă la jumătate coarda și apoi lega cele două părți formate. Apoi, ea a devenit destul de lungă, și din fericire m-am dus de-a lungul-l în jos. " Cum a reușit naratorul să facă acest lucru?
97. Interlocutorul vă cere să concepeți orice număr de trei cifre și apoi vă propune să notați numerele sale în ordine inversă pentru a obține un alt număr de trei cifre. De exemplu, 528-825, 439-934, etc. Mai mult, el cere mai mult să ia mai puțin de la el și să-i dea ultima cifră a diferenței. Apoi el numește diferența. Cum o face el?
98. Șapte au ieșit - s-au găsit șapte ruble. Dacă nu erau pentru cei șapte, dar pentru cei trei, ar fi găsit multe?
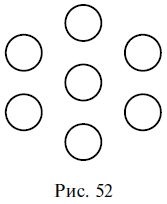
99. Împărțiți modelul, format din șapte cercuri, în trei linii drepte în șapte părți astfel încât să existe un cerc în fiecare parte (Figura 52).
100. Globul a fost tras de un cerc de-a lungul ecuatorului. Apoi, lungimea cojii a fost mărită cu 10 metri. În același timp, sa format un mic spațiu între suprafața globului și cerc. Poate un om să se târască în acest gol? Lungimea ecuatorului pământului este de aproximativ 40.000 kilometri.
1. De la primul sac nevoie pentru a scoate o monedă dintr-o a doua - doua, a treia - trei, etc. (a zecea a pungii - toate cele 10 monede) ... Apoi, ar trebui să cântăriți toate aceste monede o dată. Dacă printre ei nu a existat nici monede false, t. E., ar fi toate o greutate de 10 grame, greutatea totală de până la 550 de grame. Dar, printre monedele cântărite, se găsesc cele false (11 grame fiecare), greutatea lor totală fiind mai mare de 550 de grame. Și, dacă el este de 551 de grame, monedele contrafăcute sunt în primul sac, din cauza asta, am luat o monedă, care a dat un gram in plus. Dacă greutatea totală este de 552 grame, atunci monedele contrafăcute sunt în cea de-a doua pungă, pentru că am luat două monede din ea. În cazul în care greutatea totală este de 553 de grame, atunci, monedele false sunt în al treilea sac, și așa mai departe. D. Astfel, printr-o singură ponderare poate fi stabilită cu precizie, monede false sunt prezente în sac.
2. Este necesar să se ia cookie-urile din borcan cu semnul „cookie-uri fulgi de ovăz“ (poate fi de la orice alta). Din moment ce banca este inscripționată incorect, va fi pisică sau ciocolată. Să spunem că ai un pisat. După aceasta avem nevoie pentru a schimba etichetei „cookie-uri“ și fulgi de ovăz „shortbread“. Și din cauza stării tuturor etichetelor sunt amestecate, este acum în oala cu inscripția „Cookie-uri cu ciocolată“ este fulgi de ovăz, dar banca spune „cookie“ este ciocolata Fulgi de ovaz, atunci trebuie să facă schimb de aceste două etichete.
3. Din cabinet aveți nevoie doar de trei șosete. În acest caz, sunt posibile doar 4 variante: toate cele trei șosete sunt albe; toate cele trei șosete negre; două șosete albe, unul negru; două ciorapi negri, un alb. În fiecare dintre aceste combinații există o pereche de potrivire - albă sau neagră.
4. Ceasul lovește 12 ore în 66 de secunde. Când ceasul este lovit de 6 ore, de la prima grevă până la ultima există 5 intervale. Intervalul este de 6 secunde (1/5 din 30). Când ceasul lovește 12 ore, de la prima grevă până la ultima trece 11 intervale. Din moment ce lungimea intervalului este de 6 secunde, pentru a pumniza 12 ore, ceasul necesită 66 de secunde: 11,6 = 66.
5. Iazul va fi acoperit cu frunze de crin jumătate în ziua a 99-a. Prin condiția numărului de frunze în fiecare zi este dublat, iar în cazul în care în ziua a 99-a unui iaz acoperit de frunze în jumătate, apoi a doua zi, iar cealalta jumatate va fi acoperit de iaz frunze de crin, t. E. complet acoperit cu un iaz de 100 de zile.
6. Modul în care a trecut pe liftul pasagerului etajul al cincilea (4 interval), de două ori pe traseul parcurs de la etajul al treilea (2 zbor) marfa. Pe măsură ce ascensorul pasagerului merge de 2 ori mai repede decât ascensorul de marfă, acesta va trece simultan căile.
7. Pentru a rezolva această problemă este necesară formarea unei ecuații. Numărul de gâște din pachet este de x. "Acum, dacă am avea atât de mulți ca acum (adică x)", a spus gâștele, "atât de mulți (și anume x) și chiar jumătate (adică 1/2), da un alt sfert - atât de mult (adică 1 / 4x), și chiar de tine (de exemplu, 1 gâscă), atunci am avea 100 de gâște ". Se obține următoarea ecuație:
Adăugăm în partea stângă a ecuației:
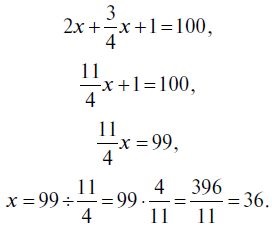
Deci, în ambalaj erau 36 de gâște.
8. Eroarea constă în construirea fiecărei părți a egalității -2 = 2 pătrat. Se creează impresia că a efectuat aceeași operațiune (cuadratura), pe fiecare parte a egalității de fapt asupra fiecărei părți a ecuației pentru a efectua diverse operații, deoarece partea stângă înmulțim cu 2, iar dreapta se înmulțește cu 2.
9. Afirmația că nucleul atomului este mai mică de 2 ori, desigur, nu este adevărat: de fapt, 10 până la 12 cm sub 10 -6 cm nu este un factor de 2, și un milion de ori.
10. Avionul în zbor "ține" în aer, deci este imposibil să zbori spre Lună, pentru că nu există aer în spațiul deschis.
11. Acul este fabricat din oțel, iar moneda este din cupru. Oțelul este mult mai greu decât cuprul, și, prin urmare, este posibil să se străpunge valoarea acului. Numai tu nu poți să faci asta manual. În cazul în care, cu toate acestea, încercați să înscrie un ac într-o monedă ciocan, de asemenea, nu funcționează: capătul ascuțit al zonei acului este atât de mică încât vârful vibreaza, diapozitive pe suprafața monedei. Pentru un ac să fie stabil, este necesar de a conduce cu un ciocan într-o monedă printr-o bucată de săpun, ceară sau lemn, acest material va da un permanent și ac în direcția corectă, și în acest caz va trece liber prin moneda de cupru.
12. Puteți pune mai mult de o mie de pini în pahar. În acest caz, o singură picătură de apă nu va curge din ea, dar se formează o bordură mică de apă, un "deal", deasupra marginilor paharului. Conform legii lui Archimedes, un corp scufundat în apă deplasează un volum de apă egal cu volumul corpului. Volumul unui pin este atât de mic încât volumul "coasterului" de apă deasupra suprafeței geamului este egal cu volumul de mai mult de o mie de pini.
13. Portretul descrie fiul lui Ivanov. Pentru a rezolva problema, puteți face o schemă simplă: