Forțele sunt măsura interacțiunii mecanice a corpurilor. Dacă structura este considerată izolată de corpurile înconjurătoare, atunci acțiunea acesteia din urmă se înlocuiește cu forțe numite forțe externe. Forțele externe care acționează asupra corpului pot fi împărțite în forțe active (independente) și reactive. Eforturile reactive apar în conexiunile impuse corpului și sunt determinate de forțele active care acționează asupra corpului.
Prin metoda de aplicare, forțele externe sunt împărțite în voluminoase și superficiale.
Forțele de volum sunt distribuite în întregul volum al corpului luate în considerare și aplicate fiecărei particule. În particular, forțele de volum sunt greutatea intrinsecă a structurii, atracția magnetică sau forțele de inerție. Unitatea de măsură a forțelor de volum este forța pe unitate de volum - kN / m 3.
Forțele de suprafață sunt aplicate pe suprafețele de suprafață și sunt rezultatul interacțiunii directe de contact a obiectului examinat cu corpurile din jur. În funcție de raportul ariei de aplicare a sarcinii și a suprafeței totale a corpului în cauză, încărcăturile de suprafață sunt subdivizate în concentrate și distribuite. Primul grup de purtat pe sarcină, aria efectivă a cererii care nesoiz-Merimee mai mică decât suprafața totală a corpului (de exemplu, OMS-efect coloane pe placa de fundație timp hexameri suficient de mari poate fi considerată ca o acțiune în efortul ei concentrată). Dacă zona de aplicare a sarcinii este comparabilă cu suprafața corpului, atunci o astfel de încărcătură este considerată distribuită. Un exemplu este greutatea fasciculului în sine, efectul încărcării de zăpadă sau vântului asupra structurii, presiunea lichidului din rezervor. De asemenea, sarcina distribuită poate acționa de-a lungul unei linii, de exemplu atunci când doi cilindri sunt în contact cu aranjamentul paralel al axelor lor. Forțele concentrate sunt măsurate în kN, iar forțele distribuite sunt măsurate în kN / m 2 sau kN / m.
În momentul acțiunii, forțele externe (forțele) sunt împărțite în permanență și temporar. Greutatea proprie a clădirii este o sarcină constantă; trenul care trece prin pod este o sarcină temporară.
Prin natura schimbării în vigoare în timp, se disting încărcările statice și dinamice. Sarcina statică (constantă) - cele care schimbă mărimea lor sau punctului de aplicație (direcția), cu o rată foarte scăzută, astfel încât accelerația rezultată (forțele de inerție) pot fi neglijate. Încărcări dinamice - variază în funcție de timp la o viteză mare, având forțe inerțiale de luat în considerare, deoarece ele au un efect semnificativ asupra designului.
Interacțiunea dintre părțile corpului examinat este caracterizată de forțe interne care apar în interiorul corpului sub influența sarcinilor externe și sunt determinate de forțele acțiunii intermoleculare. Aceste forțe rezistă dorinței forțelor externe de a distruge elementul structural, de a-și schimba forma, de a separa o parte de cealaltă.
În fascicul, secțiunea transversală este perpendiculară pe axa sa. Această secțiune este numită transversală.
Valorile forțelor interne sunt determinate folosind metoda secțiunii transversale, esența căreia este după cum urmează. În cazul în care acțiunea forțelor externe, corpul este într-o stare de echilibru, atunci orice parte a corpului rupt cu venirea la forțele sale externe și interne este, de asemenea, în echilibru, prin urmare, se aplică acestuia echilibrul ecuației.
Luați în considerare un corp având forma unei bare (Figura 1.4, a).
Să se aplice un anumit sistem de forțe externe P1, P2. P3. Pn. satisfacerea condițiilor de echilibru, adică Când forțele externe au acționat, corpul este într-o stare de echilibru.
Dacă tăiați bara A în două părți și rotiți-o pe cea dreaptă, atunci, din moment ce legătura între părți ale corpului sunt eliminate, acesta trebuie să fie acțiunea corectă (îndepărtat) porțiunea din stânga a înlocui forțele interne anumit sistem (PA) care funcționează în secțiunea A (Fig. 1.4b).
Se indică prin s, i sumele forțelor externe aplicate, respectiv, laturilor stînga s, i drepte ale barei (cu referire la secțiunea A) s, i ținând seama de faptul că
pentru părțile tăiate ale fasciculului se obțin următoarele relații evidente:
Ultimele relații arată că rezultatul forțelor interne ale RA în secțiunea A poate fi determinat cu succes egal de condițiile de echilibru ale părților stângi sau drepte ale corpului împrăștiat. Aceasta este esența metodei secțiunii.
Forțele interne trebuie să fie distribuite în lungul secțiunii astfel încât suprafețele deformate ale secțiunii A cu coincidența părților drepte și stângi ale corpului să coincidă exact. Această cerință în mecanica unui corp deformabil solid se numește starea de continuitate a deformațiilor.
Noi folosim reguli statice și de a reduce forța de sistem-vnut nal la centrul de greutate al secțiunii A, în conformitate cu regulile mecanicii teoretice. Rezultatul este vectorul principal al forțelor și vectorul principal al timpului (fig. 1.5). Următoarea xyz selectarea rd sistem de coordonate cartezian cu originea-yuschim coincide cu centroidul secțiunea transversală A. Axa este direcționată de-a lungul normalei la secțiunea transversală și axa și este situată în planul secțiunii. Proiectarea vectorului de forță principal și a momentului principal pe axele de coordonate ale lui x. y. z. obținem șase componente: trei forțe Nz. QX. Qy și trei momente Mz. Mx. Mea. numiți factori de forță interni în secțiunea transversală a fasciculului.
Se consideră că componenta Nz este normală. sau forță longitudinală în secțiune transversală. Forțele Qx și Qy sunt numite forțe transversale. Momentul Mz este numit cuplul. iar momentele Mx și My sunt momente de îndoire în raport cu axele x și y. respectiv.
Cu forțele externe cunoscute, toți cei șase factori de forță interni în secțiune transversală sunt determinați din cele șase ecuații de echilibru care pot fi trase pentru partea de tăiere.
Să presupunem că R *. M * - forța rezultantă și momentul rezultat care acționează asupra părților corpului retezate. În cazul în care organismul este în echilibru, condițiile de echilibru ale părților retezate ale corpului prin acțiunea unui sistem complet de forțe externe este după cum urmează:
Ultimele două ecuații vectoriale de echilibru dau șase ecuații scalare în proiecțiile de pe axele de coordonate carteziene:
care, în general, constituie un sistem închis de ecuații algebrice în ceea ce privește șase forțe interne necunoscute:. . . . .
În consecință, dacă sistemul total de forțe externe este cunoscut, atunci prin metoda secțiunilor, este întotdeauna posibil să se determine toate forțele interne care acționează într-o secțiune luată arbitrar a corpului. Această dispoziție este o circumstanță fundamentală în mecanica unui corp solid deformat.
În general, toți cei șase factori de forță pot apărea într-o secțiune. Cu toate acestea, destul de des în practică, există cazuri când nu sunt disponibile eforturi interne - astfel de încărcări ale lemnului au primit nume speciale (Tabelul 1.1).
Tabelul 1.1. Cele mai simple cazuri de rezistență
Tip de stare de stres
Notă: + înseamnă prezența forței, 0 - absența acesteia.
Rezistența, în care o forță internă acționează în secțiunea transversală a barei, este convențional numită simplu. Cu acțiunea simultană a două sau mai multe forțe în secțiunea fasciculului (de exemplu, torsiune cu torsiune), rezistența barei este numită complexă.
În cele din urmă, observăm că în cazul curselor practice-chetov, pentru claritate, sunt definite în general grafice funcționale-tiile factori de putere intern coordonate relative axa direcționată de-a lungul axei longitudinale a tijei. Graficele de schimbare a forțelor interne de-a lungul axei longitudinale a tijei sunt numite diagrame.
La determinarea factorilor de forță interni, se consideră că se aplică în centrul de greutate al secțiunii. De fapt, forțele interne, care sunt rezultatul interacțiunii particulelor corpului, sunt distribuite continuu pe secțiune. Intensitatea acestor forțe în diferite puncte ale secțiunii transversale poate fi diferită. Cu o sarcină crescândă pe elementul structural, forțele interne cresc și, respectiv, crește intensitatea lor în toate punctele secțiunii. Dacă la un moment dat intensitatea forțelor interne ajunge la o anumită valoare pentru un anumit material, apare o fisură în acest moment, a cărei dezvoltare va duce la distrugerea elementului sau vor apărea deformări plastice inadmisibile. În consecință, puterea elementelor structurale ar trebui judecată nu prin valoarea factorilor de forță interni, ci prin intensitatea lor. Măsura intensității forțelor interne se numește stres.
Într-un cartier al unui punct arbitrar aparținând secțiunii unui corp încărcat, identificăm o zonă elementară. în care acționează forța internă (Figura 1.6, a).
Valoarea medie a intensității forțelor interne pe amplasament, numită stresul mediu, este determinată de formula
Scăderea zonei. în limita, obținem adevărata stres într-un anumit punct al secțiunii
O cantitate vectorială se numește tensiunea totală într-un punct. În sistemul internațional de unități (SI), unitatea de tensiune este Pascal (Pa) - tensiunea la care o forță internă de 1 N acționează pe suprafața de 1 m 2.
Deoarece această unitate este foarte mică, în calcule se utilizează o unitate de tensiune multiplă - megapascal (1 MPa = 10 6 Pa).
Se descompune vectorul tensiunii totale în două componente (figura 1.6b).
Proiecția vectorului de tensiune totală pe cel normal la o anumită zonă este marcată de tensiune normală și este denumită tensiune normală.
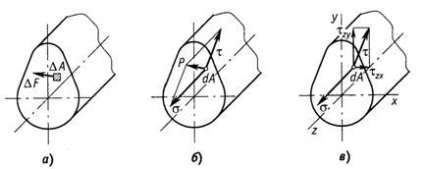
Componenta situată în secțiune într-o anumită zonă este notată de și este numită tensiunea tangențială.
Tensiunea normală direcționată din secțiunea transversală este considerată pozitivă, direcționată spre secțiunea transversală este negativă.
Stresurile normale apar atunci când, sub acțiunea forțelor exterioare, particulele situate pe ambele părți ale secțiunii tind să se îndepărteze una de cealaltă sau să se apropie reciproc. Tensiunile tangențiale apar atunci când particulele tind să se deplaseze unul față de celălalt în planul secțiunii.
Stresul tangențial poate fi descompus de-a lungul axelor coordonate în două componente și (fig.1.6, c). Primul indice care arată axa care este perpendiculară pe secțiune, al doilea - paralel cu axa pe care acționează tensiunea. Dacă în calcule direcția stresului tangențial nu contează, este desemnată fără indici.
Între întreaga tensiune și componentele sale există o dependență
Prin punctul corpului se poate trasa un număr infinit de secțiuni, iar pentru fiecare dintre ele stresul are propriul său înțeles. Prin urmare, pentru a determina tensiunile, este necesar să se indice poziția nu numai a punctului corpului, ci și a secțiunii trase prin acest punct.
Tensiunile cumulative pentru un număr de locuri care trec printr-un punct dat formează o stare de stres în acest moment.
Stresurile în secțiuni transversale sunt asociate cu factorii de forță interni de anumite dependențe.
Facem o zonă infinitezimală în secțiune. În acest caz, în cazul general, forțele interne infinitezimale (elementare) acționează (Figura 1.7)
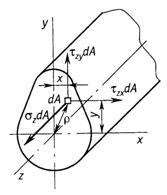
Momentele elementare corespunzătoare în raport cu axele de coordonate. . au forma:
Rezumând forțele și momentele infinit de mici care acționează în secțiunea transversală, obținem expresiile care leagă factorii forței interne cu tensiunile:
În conformitate cu teorema lui Varignon, cunoscută din mecanica teoretică, și relația dintre stres. și. expresia pentru poate fi scrisă în formă
Funcția Integral (1.8) poate fi utilizat pentru a determina solicitarea pe secțiunile găsite de factori de putere interni, cu condiția ca legile cunoscute distribuția tensiunilor pe secțiunea transversală.
Deplasări și deformări
Sub influența forțelor externe, solii își schimbă forma geometrică, adică se deformează. În cazul în care este considerat absolut rigid, atunci rezistența materialelor corpului au capacitatea de a fi deformată în mecanica teoretice ale corpului. și anume sub influența unei încărcături externe, își schimbă dimensiunile și forma inițială. Punctele corpului se mișcă astfel în moduri diferite în spațiu. Vector. având originea în punctul A nedefor-gramat de stat și în final t. stare deformată, deplasarea totală se numește vectorul t. A (fig. 1.8, a). proiecția sa pe axele xyz sunt numite mișcări axiale și sunt desemnate prin u, v și w. respectiv.
Pentru a caracteriza schimbările de intensitate în dimensiunea corpului și forma, ia în considerare un punct A și starea nedeformabil vannogo distanțate una de alta (fig. 1.8, b).
Să presupunem că, ca urmare a acestor modificări puncte peremes-tilis în forma corpului și poziția, respectiv, iar distanța dintre ele este crescut cu DS valoare și a făcut S + DS. valoare
se numește o deformare liniară la punctul A în direcția AB. Dacă luăm în considerare deformările de-a lungul direcțiilor axelor de coordonate. Indicii sunt introduși în notația proiecțiilor corespunzătoare de deformare liniară. . .
Deformări liniare. . caracterizează modificări ale volumului corpului în timpul deformării și modelarea corpului - deformări unghiulare. Pentru a le determina, luați în considerare unghiul drept format în stare nedeformată de două segmente OD și OC (Figura 1.8, b). Cu acțiunea forțelor externe, unghiul specificat DOC se va schimba și va presupune o nouă valoare. valoare
se numește deformare unghiulară. sau o schimbare la punctul O în planul CDD. În ceea ce privește axele de coordonate, se indică deformarea forfecării. . .
Setul de deformări liniare și unghiulare de-a lungul unor direcții și planuri diferite la un anumit punct formează o stare deformată într-un punct.