este considerat a fi continuu neted pe o bucată dacă funcțiile sunt continue și segmentul poate fi divizat într-un număr finit de segmente parțiale de puncte
astfel încât pe fiecare dintre ele funcțiile să aibă derivate continue care nu sunt egale cu zero în același timp.
În Fig. 64 prezintă o curbă continuă pe o bucată continuă. În puncte și este continuă, dar toate sau unele derivate suferă o discontinuitate (de primul fel!).
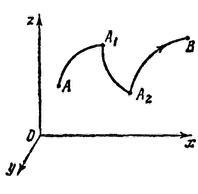
Denumim curba (1) cu o literă, de exemplu printr-o literă. De obicei, denotă nu numai locusul punctelor definite de ecuația (1), ci și ordinea acestor puncte, atunci când crește continuu de la. În acest sens, ei spun că există o curbă orientată. Ordinea succesiunii este indicată în figură cu săgeata (Figura 64) - când crește continuu de la, punctul se mișcă în direcția săgeții.
Dacă există o funcție care are un derivat pozitiv continuu pe un anumit segment și în acest caz, atunci ecuația
determină aceeași curbă orientată ca. Este notat cu aceeași literă, doar se spune în cazul ecuației (1), care este determinată de parametru, iar în cazul (1 ') - de parametru. În ambele cazuri, creșterea de la înălțime sau creștere spre punctele corespunzătoare se mișcă în aceeași direcție.
Este o altă problemă dacă faceți o înlocuire, unde există un derivat negativ continuu pe segment. În acest caz și cu o creștere continuă de la la, parametrul va scădea, iar săgeata de pe obiectul nostru geometric va trebui direcționată spre cealaltă parte.
Prin urmare, curba (1 ') în cazul în care, vom denumi cu un alt simbol și vom spune că există aceeași curbă, care, dar orientată în direcția opusă. Uneori indicăm curba orientată inițial de simbol.
O curbă orientată (1) este numită contur închis sau închis, dacă sau, care este același lucru, dacă
Cu alte cuvinte; atunci când valoarea parametrului crește continuu de la, punctul corespunzător trece printr-o cale continuă în spațiu, începând și terminând în același punct. Dacă, în același timp, curba în alte puncte nu se intersectează, atunci se numește o curbă închisă care se intersectează. În Fig. 65a, este prezentată o curbă închisă cu auto-intersectare, iar în fig. 65, 6 este o curbă închisă cu auto-intersectare.

Notă. Ecuația vectorului (1) a curbei este echivalentă cu trei ecuații
Exemplul 1. Fie curba dată prin ecuație
Deoarece, atunci această curbă este un cerc de rază cu centrul la origine. Pe măsură ce creșteți de la 0 la un punct, acesta se mișcă într-un cerc în sens invers acelor de ceasornic. În acest caz, diferite puncte corespund diferitelor puncte. Cu u avem. Prin urmare, cercul este o curbă închisă de auto-intersectare (Figura 66).
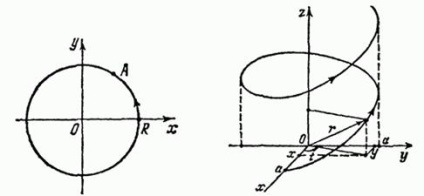
Exemplul 2. Curba
unde sunt numere pozitive, se numește helix. Se poate obține după cum urmează. Un segment de lungime perpendicular pe axă, un capăt alunecă de-a lungul axei și simultan se rotește în apropierea axei, apoi celălalt capăt al segmentului descrie linia șurubului. Noi credem că înălțimea de creștere a segmentului de-a lungul axei este proporțională cu unghiul de rotație. Pe măsură ce crește punctul, se mișcă, așa cum se arată în Fig. 67. Este evident că linia de șurub este localizată pe suprafața laterală a unui cilindru circular de rază, cu o generatoare paralelă cu axa.