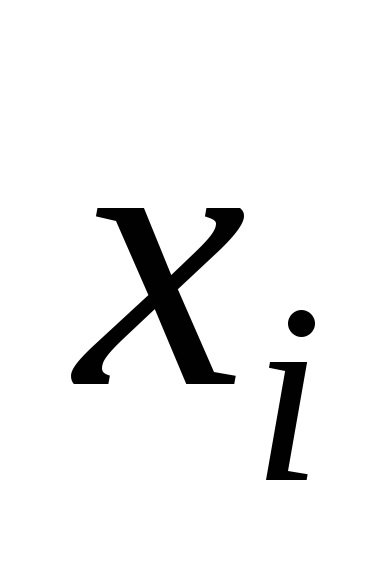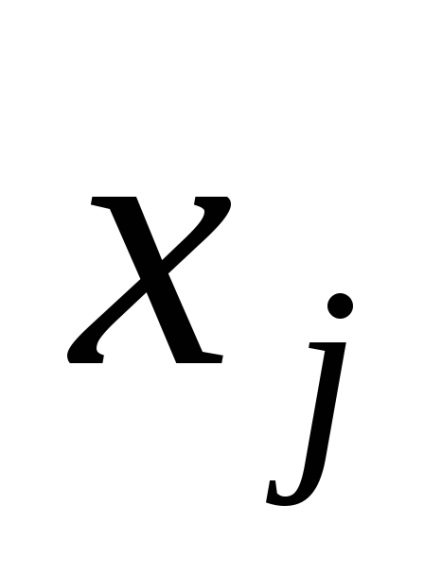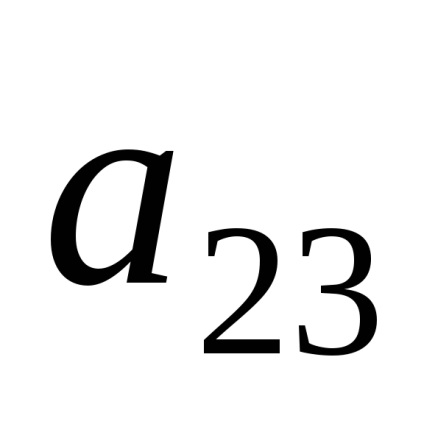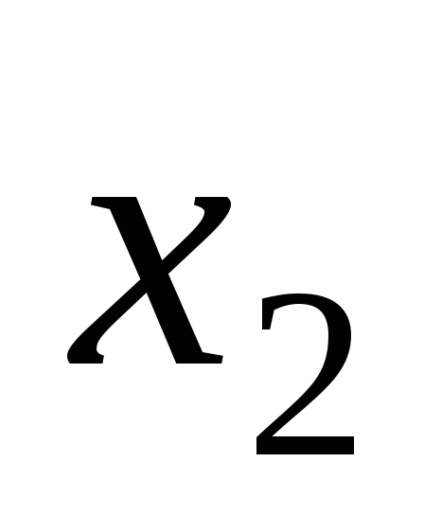Seturi și relații.
Seturi și specificațiile acestora. Operații pe seturi. Diagramele lui Euler-Venn. Puterea setului. Seturi finite și numărate. Relația. Proprietățile relațiilor. Operațiuni peste relații. Relația de echivalență. Bătăi și relația de echivalență. Relații ordonate parțiale și stricte. Funcții și mapări. Injectarea, surjecția, suprapunerea, bijecția, funcțiile inverse.
Referințe: [1], p. 5-10; [3], partea 2; [4], Ch. 1-3; [5], Ch. 1.
Algebre booleene. Elemente ale logicii matematice.
Funcțiile booleene. Metode ale sarcinii. Variabile esențiale și fictive. Formule booleene. Proprietățile de bază ale operațiilor logice. Forme normale perfecte. Polynom Zhegalkin. Clase închise de funcții. Sisteme complet funcționale. Teoreme privind completitudinea funcțională. Exemple de baze funcționale complete. Problema minimizării funcțiilor booleene. Scheme de elemente funcționale. Mașini de stat finite. Teorii formale. Conceptul de expresie. Tautologie. Calculul propozițiilor. Logica predicatelor.
Referințe: [1], p. 14-53; [2], Ch. 3.8; [3], pct. 1.4; [4], Ch. 4, 5; [5], Ch. 3.4.
Echivalența formulelor booleene.
Funcțiile booleene pot fi specificate fie folosind tabelele de adevăr (unic), fie folosind formule logice (unic). Dacă tabelele de adevăr ale două formule booleene coincid, atunci aceste formule sunt echivalente și definesc aceeași funcție booleană.
Un exemplu. Verificați echivalența formulelor booleene:
.
Construim masa adevărului pentru funcție.
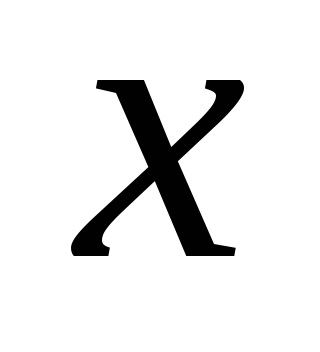
Coloanele rezultate în tabelele de adevăr sunt aceleași, prin urmare, formulele sunt echivalente.
Variabile esențiale și fictive.
variabil
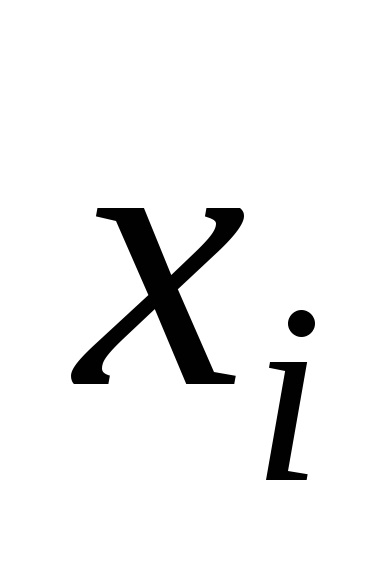
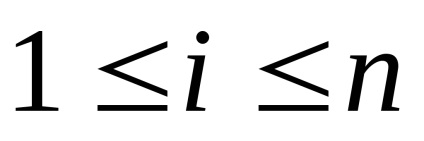
pentru orice valori ale variabilelor. În caz contrar, variabila
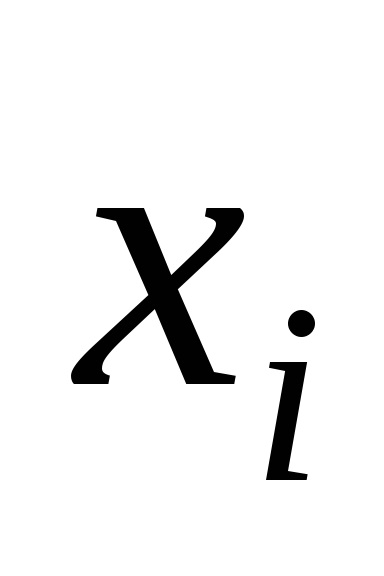
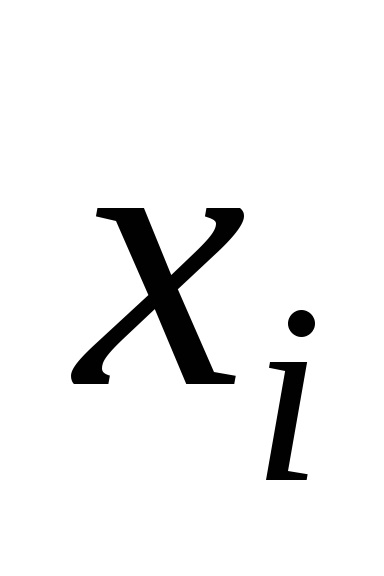
Un exemplu. Identificați variabilele de funcții esențiale și funcționale (11110011).
Pentru comoditate, prezentăm tabelul de adevăr.
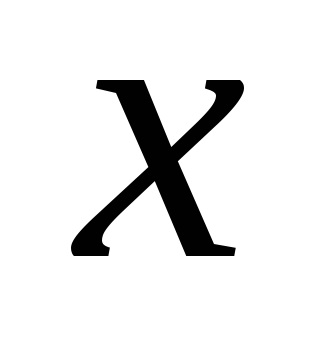

Matricea de contiguitate
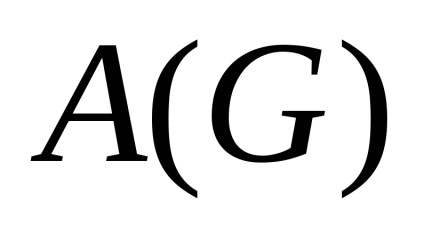

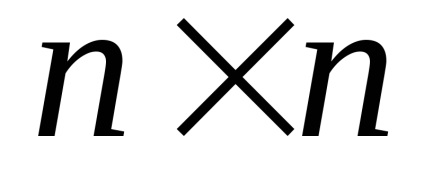
Matricea de adjuvant pentru un grafic dat are forma:

Matricea incidenței
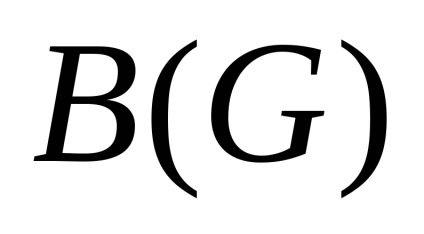

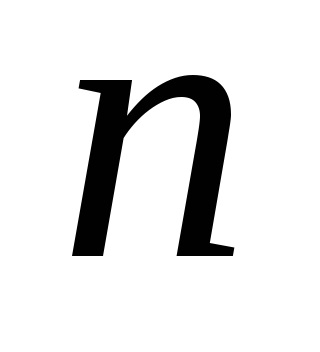
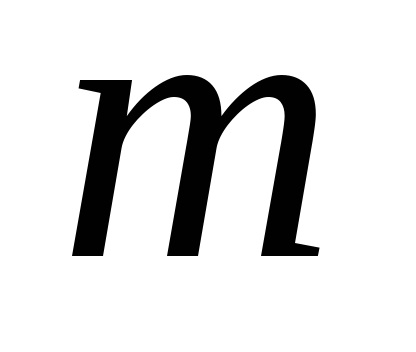

În coloană