3. Un sistem plan de forțe arbitrar localizate
Forța aplicată unui corp complet solid, nu poate avea un efect de schimbare, muta paralel cu ea însăși, în orice parte a corpului, adăugând în același timp, cu un cuplu de moment, egal cu momentul puterii portabile în raport cu punctul în care este transferată forța (Fig. 10).
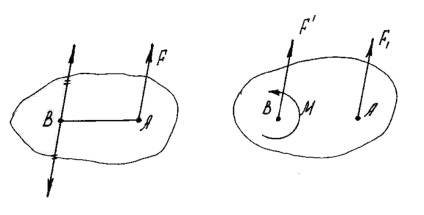
Fiecare sistem plan al forțelor care acționează asupra unui corp rigid, atunci când este activat de către un centru arbitrar ales O înlocuiește o singură forță R. sistem egal vector principal și aplicat pentru a aduce centrul O. și o pereche cu un cuplu MO. egală cu momentul principal al sistemului în raport cu centrul O (figura 11).
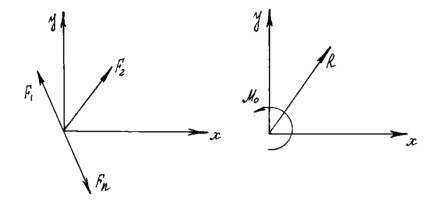
Cazurile particulare de a aduce un sistem plat de forțe în cea mai simplă formă:
- dacă pentru un anumit sistem de forțe R = 0 și MO = 0, atunci este în echilibru;
- Dacă pentru un anumit sistem de forțe R ≠ 0, M = 0, atunci acesta este redus la un rezultat.
Forma de bază a condițiilor de echilibru. Pentru echilibrul unui sistem de forțe arbitrar de forțe este necesar și suficient ca suma proeminențelor tuturor forțelor pe fiecare dintre cele două axe de coordonate și suma momentelor lor față de orice centru situată în planul de acțiune al forțelor să fie zero.
A doua formă de condiții de echilibru. Pentru echilibrul unui sistem de forță plană arbitrară, este necesar și suficient ca suma momentelor tuturor acestor forțe față de oricare două centre A și B și suma proeminențelor lor pe axa Ox. Nu este perpendiculară pe linia AB. au fost egale cu zero.
Cea de-a treia formă de condiții de echilibru. Pentru echilibrul unui sistem de forțe arbitrar al forțelor, este necesar și suficient ca suma momentelor tuturor acestor forțe față de oricare trei centre de AVS care nu se află pe aceeași linie să fie egală cu zero.
4. Conceptul de fermă. Calculul fermelor
Structura este o structură rigidă de tije rectilinii conectate la capete prin balamale (Figura 12).
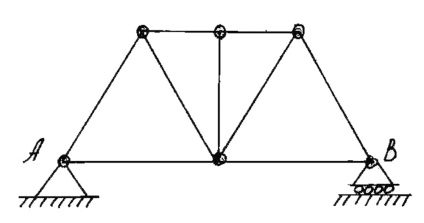
Dacă toate barele de fermă se află în același plan, ferma este numită plat.
Punctele de joncțiune ale zonelor de fermă sunt numite noduri.
Tijele înclinate sunt numite armături. vertical - cu rafturi.
Distanța dintre două suporturi se numește o deschidere.
Calculul fermelor se realizează prin două metode:
1) metoda de tăiere a nodurilor. ceea ce reduce la o examinare consecventă a condițiilor de echilibru a forțelor convergente la fiecare dintre nodurile fermei;
2) metoda secțiunii transversale (metoda Ritter), care constă în împărțirea structurii în două părți printr-o secțiune care trece prin trei tije, în care este necesară determinarea forței care formează ecuațiile de echilibru.
5. Sistemul forței spațiale
Momentul forței raportat la axă este o cantitate scalară egală cu momentul proiecției acestei forțe pe un plan perpendicular pe axa luată față de punctul de intersecție al axei cu planul.
Pentru a afla momentul forței în raport cu axa Z (figura 13), este necesar:
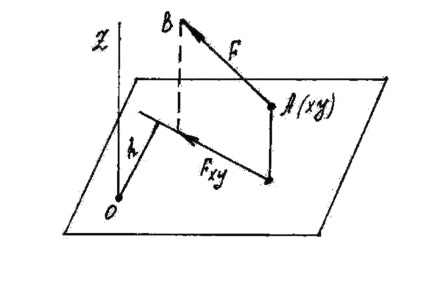
1) trageți planul xy. perpendicular pe axa z;
2) proiectați forța F pe acest plan și calculați valoarea Fxy;
3) omiteți perpendicularul pe direcția Fxy și lungimea lui h din punctul O al intersecției axei cu planul;
5) determina semnul momentului.
Cazuri particulare în determinarea momentului:
1) dacă forța este paralelă cu axa, atunci impulsul său unghiular față de axă este zero, deoarece Fxy = 0;
2) dacă linia de acțiune a forței traversează axa, atunci impulsul său angular față de axă este de asemenea zero, deoarece h = 0;
3) dacă forța este perpendiculară pe axă, atunci impulsul său unghiular față de axă este egal cu produsul modulului de forță prin distanța dintre forță și axă.
Condiții de echilibru a unui sistem spațial arbitrar de forțe. Pentru echilibrul unui sistem de forță spațială arbitrară este necesar și suficient ca sumele proiecțiilor tuturor forțelor pe fiecare dintre cele trei axe de coordonate și suma momentelor lor în raport cu aceste axe să fie zero.
II. Cinematica unui punct și a unui corp rigid
1. Concepte de bază ale cinematicii
1.1. Metode pentru specificarea mișcării unui punct
Cinematica este diviziunea mecanicii, în care proprietățile geometrice ale mișcării corpurilor sunt studiate fără a ține seama de inerția (masa) și de forțele care acționează asupra lor.
Din punct de vedere cinematic, mișcarea sau legea mișcării unui corp (puncte) înseamnă stabilirea poziției acestui corp (punct) în raport cu un cadru de referință dat în orice moment.
Un sistem de referință este un corp solid sau condiționat, în raport cu care se determină poziția altor corpuri mobile.
Modul natural de a stabili mișcarea. O linie continuă, care descrie un punct de deplasare relativ la un cadru de referință dat, se numește traiectoria unui punct. Dacă traiectoria este o linie dreaptă, mișcarea unui punct este numită rectilinie și dacă curba este curbila.
Legea de mișcare a unui punct de-a lungul unei traiectorii este exprimată de ecuația S = f (t).
Pentru a specifica mișcarea unui punct într-un mod natural, trebuie să știm:
1) traiectoria punctului;
2) originea referinței pe traiectorie care indică direcțiile de referință pozitive și negative;
3) legea de mișcare a unui punct de-a lungul unei traiectorii sub forma S = f (t).
Valoarea numerică a vitezei unui punct la o anumită clipă de timp este egală cu prima derivată a distanței punctului în timp:
Valoarea numerică a accelerației unui punct la un moment dat este egală cu prima derivată a vitezei:
Metoda coordonată pentru specificarea mișcării
Legea mișcării unui punct sub metoda coordonatelor este exprimată prin ecuațiile:
Proiecțiile de viteză pe axa coordonatelor sunt egale cu primele derivate ale coordonatelor corespunzătoare ale punctului în timp:
Proiecțiile accelerației pe axa coordonatelor sunt egale cu primele derivate ale proiecțiilor de viteză sau de al doilea derivat al coordonatelor corespunzătoare ale punctului în timp.
1.2. Accelerare punctuală și tangențială
Proiecția accelerației unui punct pe tangent la traiectoria sa se numește accelerația tangențială sau tangențială a.
Proiecția accelerației la normal se numește accelerația normală a.
Accelerația tangențială și normală (Figura 14) nu este considerată ca o proiecție, ci ca o componentă a unei accelerații complete. adică, ca vectori, iar accelerația totală va fi egală cu
Componenta tangențială este tangențială, ca vectorul de viteză V. Prin urmare, nu poate afecta direcția vitezei, dar afectează magnitudinea ei.
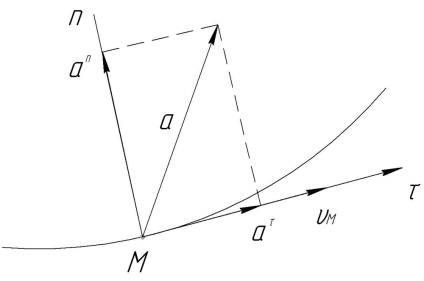
Componenta normală este direcționată perpendicular pe vectorul de viteză și, prin urmare, nu poate afecta magnitudinea vitezei, dar afectează direcția acesteia.
, unde ρ este raza de curbură.
2. Mișcarea progresivă și rotativă a unui corp rigid
Progresiv este mișcarea unui corp rigid, în care orice linie dreaptă trasă în acest corp se mișcă, rămânând paralelă cu ea însăși.
În mișcarea de translație, toate punctele corpului descriu traiectoriile identice (când se suprapun) și au la fiecare moment al timpului viteze și accelerații care sunt aceleași în mărime și direcție.
Pentru mișcarea translațională, viteza V comună pentru toate punctele corpului se numește viteza mișcării translaționale a corpului. și accelerația a este accelerarea mișcării translaționale.
Rotația este o mișcare a unui corp rigid în care oricare două puncte care aparțin corpului (sau invariabil asociate cu acesta) rămân nemișcate în orice moment.
O linie dreaptă care trece prin două puncte fixe se numește axa de rotație.
Ecuația γ = f (t) exprimă legea mișcării de rotație a unui corp rigid. unde γ este unghiul de rotație a corpului.
Principalele caracteristici cinematice ale mișcării de rotație a unui corp rigid sunt viteza unghiulară ω și accelerația unghiulară ε.
Viteza unghiulară a unui corp la un anumit moment de timp este numeric egală cu prima derivată a unghiului de rotație în raport cu timpul:
Accelerarea unghiulară a unui corp la o anumită clipă de timp este numeric egală cu prima derivată a vitezei unghiulare sau a celui de-al doilea derivat al unghiului de rotație a corpului în raport cu timpul:
Dacă modulul de viteză unghiulară crește cu timpul, rotația corpului se numește accelerată. și dacă scade - încetinită.
Dacă viteza unghiulară a corpului rămâne constantă pe toată durata mișcării (ω = const), atunci rotația corpului se numește uniformă.
Dacă accelerația unghiulară a corpului în orice moment al mișcării este constantă (ε = const), atunci rotația se numește echicontinuă.
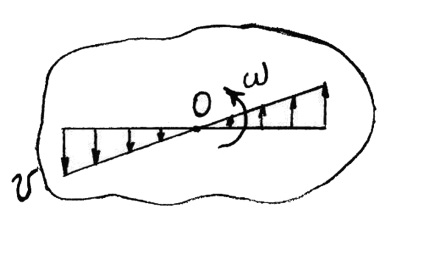
Viteza liniară a unui punct v al unui corp rigid rotativ este numeric egal cu produsul vitezei unghiulare a corpului ω cu o distanță R de la acest punct la axa de rotație.
Viteza liniară este tangentă la punctul circumscris sau perpendicular pe planul care trece prin axa de rotație.
Deoarece pentru toate punctele corpului viteza unghiulară ω are aceeași valoare la momentul dat, rezultă că vitezele liniare ale punctelor corpului rotativ sunt proporționale cu distanțele lor față de axa de rotație (Figura 15).
Accelerația tangențială a este îndreptată de-a lungul tangentei spre traiectorie (spre mișcare dacă corpul se rotește cu viteză accelerată sau în direcția opusă dacă corpul se rotește încet); accelerația normală a este întotdeauna direcționată de-a lungul razei R pe axa de rotație (Figura 16).
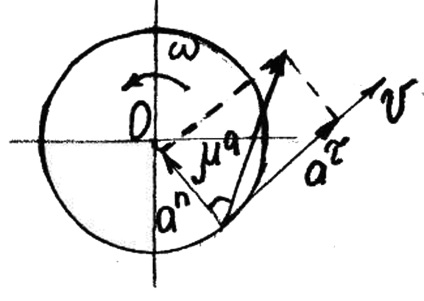
Accelerația totală a punctului este a = R.
Abaterea vectorului de accelerație totală de la raza descrisă de punctul cercului este determinată de unghiul μ, care este calculat prin formula: