ε = φ = ω (rad / sec 2) sau (s -2)
Dacă primul și al doilea derivat al unghiului φ în raport cu timpul au același semn, atunci rotația este accelerată, dacă semnul diferit este apoi lent. Dacă viteza unghiulară este constantă, atunci rotația este uniformă (cu accelerația unghiulară ε = 0).
2.2.2. Viteza și accelerarea punctului corpului rotativ
Viteza de mișcare a unui punct al corpului de-a lungul unui cerc se numește viteza de rotație, iar modulul său depinde de distanța de la punct la axa de rotație.
Vectorul de viteză este direcționat perpendicular pe raza cercului descrisă de punct în direcția de rotație (figura 2).
Accelerarea punctului corpului rotativ are două componente - accelerația centripetală și rotațională.
A cc = ω 2 ОМ și vр = ε ОМ
Vectorul a este direcționat de la punctul la axa de rotație și vectorul este direcționat perpendicular pe raza în direcția.
Vectorul de accelerație totală a este egal cu suma geometrică a cc și a
iar modulul de accelerație absolută este determinat de formula
2.2.3. Exprimarea vectorială a vitezei, accelerației centripetale și a rotației punctelor unui corp rotativ
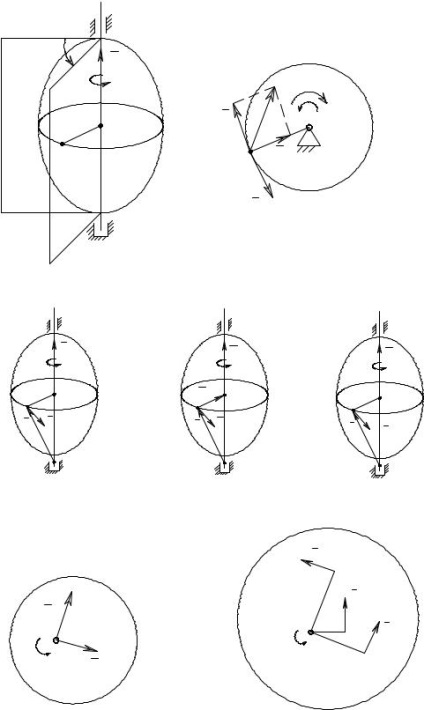
Se crede că viteza unghiulară și accelerația unghiulară - sunt vectori îndreptate de-a lungul axei rotației, w vectorul este direcționat de-a lungul axei, astfel încât rotația sa finală părea care apare în sens antiorar, unghiular gruparea e vectorul accelerație, de asemenea, direcționată de-a lungul axei aceeași partea în care ω este cu rotație accelerată sau în direcția opusă - atunci când rotația este lentă.
Viteza de rotație a punctului, accelerația centripetală și rotațională poate fi reprezentată ca produse vectoriale (figura 3).
a cc = ω x v = ω x ω x r