Un patrulater este o figură geometrică care are patru noduri și patru laturi care leagă succesiv aceste noduri.
Luați în considerare un ABCD quadrilateral arbitrar.
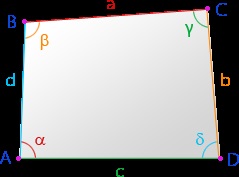
α. β. γ. δ sunt unghiurile cvadranglei
A. B. C. D - vârfurile patrulaterului
În funcție de paralelismul (⊥) laturilor opuse (a.c și b.d), lungimile acestor laturi și unghiurile α. β. γ. δ. se disting următoarele tipuri de cvadrangle:
- paralelogram. în cazul în care părțile opuse ale patrulaterului sunt paralele (a ǁ c. b ǁ d) și egale între ele (a = c. b = d), în care unghiurile opuse ale patrulaterului sunt egale între ele, dar nu în direct (α = γ ≠ 90 de grade, β = δ ≠ 90 de grade);
- dreptunghi, în cazul în care laturile opuse ale patrulaterului sunt paralele (a ǁ c b ǁ d.), egale între ele (a = c b = d.), dar toate colțurile patrulater directe (α = β = γ = δ = 90 °);
- pătrat. (A. ǁ c b ǁ d) în cazul în care părțile opuse ale patrulaterului sunt paralele, toate laturile sunt egale între ele (a = b = c = d) și toate colțurile patrulaterului directe (α = β = γ = δ = 90 grade);
- romburi. în cazul în care părțile opuse ale patrulaterului sunt paralele (a ǁ c. b ǁ d), toate părțile sunt egale între ele (a = b = c = d), în care unghiurile opuse ale patrulaterului sunt egale între ele, dar nu în directă (α = γ ≠ 90 grade , β = δ ≠ 90 de grade);
- trapez. dacă numai două laturi ale patrulaterului sunt paralele (a ⊥ c), dar nu sunt egale între ele (a ≠ c)