După descoperirea supraconductivității, s-au făcut multe încercări de a explica astfel de efecte neobișnuite ale supracodicității. Dintre aceste lucrări, multe teorii au păstrat încă semnificația lor. Astfel, în 1935, F. și G. Londra, folosind modelul cu două fluide, au obținut așa-numitele ecuații din Londra. explicând multe proprietăți macroscopice ale supraconductorilor.
În 1950, V.L. Ginzburg și L.D. Landau a construit o teorie a superconductivității bazată pe mecanica cuantică. Prin rezolvarea ecuațiilor Ginzburg-Landau, s-au explicat și s-au prezis multe proprietăți ale supraconductoarelor, inclusiv diamagnetismul ideal, cuantificarea fluxului magnetic și o serie de altele.
În ciuda faptului că teoria Ginzburg - Landau, a fost dezvoltat în continuare în lucrările lui AA Abrikosov și LP Gor, a descris multe dintre proprietățile supraconductoare, nu a putut explica fenomenul de supraconductibilitate la nivel microscopic.
Cooper a arătat că, în prezența atracției dintre electroni, chiar și în mod arbitrar mic, starea normală a sistemului cu multe electroni devine instabilă datorită procesului de asociere. Electronii cu momente opuse și rotiri antiparalerale sunt combinate în perechi Cooper. Ei au energie mai mică decât electronii normali individuali.
Să ne gândim cum se realizează atracția între particulele încărcate de electroni. Grinzile de cristal constau din ioni pozitivi, care atrag electroni. Dar electronii atrag de asemenea ioni, deplasându-i din poziția de echilibru. Această deplasare este nesemnificativă datorită diferenței enorme a masei ionului și electronului, dar există: așa cum se spune, rețeaua este polarizată. Astfel de deplasări de sarcină perturbe omogenitatea câmpului ionic și pot fi interpretate ca apariția unei încărcări pozitive. Această taxă virtuală atrage un alt electron situat în apropiere. Regiunea de polarizare a rețelei nu este fixă, se mișcă împreună cu electronul care o formează. Dacă o astfel de atracție prevalează asupra repulsiei Coulomb, electronii formează perechi. Interacțiunea electronilor printr-o latură poate fi reprezentată ca urmare a emisiei unui fonon de către un electron și a absorbției de către un altul (figura 5.11, a).
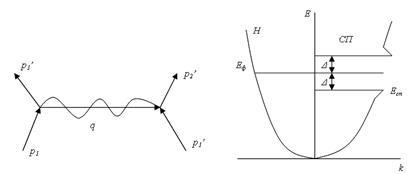
Fig. 5.11. Formarea perechilor Cooper: a - emisie și absorbție de electroni
fonon; b - spectrul unui superconductor
Fie T = 0K și în cristal nu există fononi de zăbrele. Primul electron emite un fonon cu impuls. care este absorbit de cel de-al doilea electron. Electronii după interacțiune schimbă impulsurile asupra și. În acest caz, legea conservării momentei
sau, respectiv, pentru vectorii de undă
în cazul în care. - vectori de undă ai electronilor înainte de interacțiune;
. Vectorii după interacțiune.
Phonon q. despre care vorbim - un fonon neobișnuit, virtual. Spre deosebire de cele obișnuite, nu se mișcă liber de-a lungul laturii, ci numai de la un electron la altul. După cum am arătat deja, la zero temperatura nu există fononi obișnuiți în zăbrele.
Deoarece perechea Cooper conține electroni cu roti antiparalel, are spin zero și este un boson. Conform distribuției Bose-Einstein, toate perechile ocupă nivelul EF- # 916; (Figura 5.11, b). Figura arată pentru comparație spectrele de energie ale fazelor normale (partea stângă) și superconductoare. După cum se poate observa în starea SP, spectrul de energie are un spațiu de lățime egal cu energia de legare a perechii 2 # 916; La T ≈ 0, lățimea spațiului energetic este maximă și egală cu
unde k este constanta Boltzmann.
Existența unui decalaj energetic a fost confirmată experimental, în particular, în studiul spectrului de absorbție al unui superconductor în regiunea IR de departe. La o frecvență pentru care h # 957; = 2 # 916; absorbția intensivă a radiațiilor începe. Energia 2 # 916; este cheltuit pentru ruperea perechii. Cu o creștere a temperaturii, este posibil ca electronii să traverseze spațiul și să formeze electroni nepermani deasupra lui. Decalajul scade, iar la T = TC diferența dispare.
În apropierea TS, decalajul energetic variază în funcție de temperatură, conform expresiei
Estimăm dimensiunile perechii Cooper # 958; 0 și fracțiunea lor nS în numărul total de electroni. Pentru valorile tipice ale SP: EF = 10 eV, kF = 10 8 cm -1 și TC = 10K, obținem # 958; ≈ 10 -4 cm, ceea ce înseamnă că electronii din pereche sunt separați de 10 3 ... 10 4 perioade ale rețelei de cristal.
Concentrația perechilor Cooper la T = 0K poate fi determinată prin integrarea expresiei (5.70). Acesta este de 10 -4 din concentrația totală de electroni liberi. Cu o temperatură în creștere, această concentrație scade și la T = TC, nS = 0.
Așa cum am menționat deja, spre deosebire de electronii-fermioni individuali, perechile Cooper sunt bosoni. Pentru ei nu există nici un postulat al interzicerii lui Pauli, Cuplurile Cooper sunt în aceeași stare și corespund între ele în toți parametrii fizici. Funcțiile de undă ale SP ale electronilor sunt coerente, adică fazele lor diferă între ele printr-o valoare constantă. Astfel, perechile Cooper ("condens Bose") sunt un ansamblu interconectat.
Într-un câmp electric, perechile Cooper vor fi accelerate, adică pentru a primi un impuls rezultat din cauza interdependenței dintre perechi. Acest impuls ar trebui să fie exact același pentru toate perechile. Cu toate acestea, perechea nu poate schimba energia cu grila, altfel va trece într-o altă stare de energie, care este interzisă de condițiile modelului. Din punct de vedere figurativ, ansamblul preia această interacțiune și, atâta timp cât nu este mare, se păstrează întregul impuls al ansamblului, adică curentul electric nu se schimbă. Aceasta înseamnă că transferul încărcării prin grilaj se face fără rezistență.
Dacă energia impactului devine mai mare decât energia de legare (T> TC, j> jC, B> BC), atunci cuplarea perechii se prăbușește și se lasă condensatul cuantic Bose.
Teoria BCS a fundamentat multe relații empirice în superconductivitate.
Deasupra am considerat proprietățile superconductoarelor obișnuite cu temperatură joasă (vezi Tabelul 5.1). Aici este necesar să spunem despre principalele diferențe care au supraconductori de temperatură ridicată.
1. O valoare ridicată a temperaturii de tranziție se află în regiunea temperaturilor azotului (T> 77 K), ceea ce nu este explicat de teoria actuală a BCS.
2. Legături chimice ale HTSC. Spre deosebire de NTSC care au legături metalice (metale, aliaje) sau chimice covalent (semiconductori), HTSC sunt oxizi. Natura legăturii conduce la faptul că în astfel de supraconductori densitatea transportoarelor este mai mică.
3. Rezistența normală (T> TC) a compușilor HTSC este mult mai mare. decât în metalele obișnuite și depinde puternic de conținutul de oxigen.
4. Spre deosebire de convenționale LTSC unde ia tranziția de temperatură de cel mult 1 ... 2K în această tranziție mai HTSCs 4K și depinde de metoda de preparare a probei
5. Lungimea coerenței Ginzburg-Landau în HTSC este
10 -6 m. Pentru HTSC această valoare este mult mai mică - 0,5 ... 30 °. Reamintim că lungimea coerenței caracterizează distanțele pe care densitatea perechilor superconductoare variază. O valoare atât de mică a lungimii de coerență în HTSC duce la fenomene neobișnuite. În particular, defectele bidimensionale (de suprafață) în HTSC pot forma bariere Josephson.
Acestea și alte observații conduc la concluzia că, în procedeele convenționale HTS similare, dar există diferențe legate în principal, cu o lungime de coerență mică, o mare adâncime de penetrare a câmpului magnetic, etc. care trebuie luate în considerare la proiectarea dispozitivelor pentru microelectronica superconductoare la temperaturi înalte. Unele aplicații posibile ale efectelor superconductivității în criomicroelectronică vor fi luate în considerare mai jos (§ 10.2).