Rata incidenței particulelor într-un mediu depinde de dimensiunea, forma, densitatea și densitatea mediului. Particulele mai mari cu densitate mare cad mai repede decât particulele mici cu densitate scăzută. Cu toate acestea, rata incidenței unei particule mari cu o densitate mare poate fi redusă semnificativ dacă are o formă plană, deoarece în acest caz rezistența mediului crește.
Există două tipuri principale de rezistență medie: dinamică și vâscoasă.
Ambele tipuri de rezistență afectează rata de incidență a particulelor sub clasificare hidraulică, dar gradul de manifestare a acestora atunci când diferitele boabe cad, nu este același.
Atunci când particulele mari cad la viteză mare, rezistența dinamică predomină și când particulele mici cad, vâscozitatea este vâscoasă.
Rata finală de cădere în ...
apă Boabe mai mari de 1 mm pot fi determinate prin formula Ritterer
# 965; 0 = R 1000), (4.1)
unde R este coeficientul numeric (pentru apa R = 0,16, pentru aer R = 4,6); d este diametrul granulei sferice, m; # 948; - densitatea cerealelor, kg / m3.
Pentru boabele mai mici de 0,1 mm, rata finală de incidență este determinată de formula Stokes
unde S este coeficientul numeric (pentru apa S = 545, pentru aer S = 30278).
Pentru a determina rata finală de incidență a boabelor de dimensiune intermediară (0,1 - 1 mm), formula lui Allen
unde A este un coeficient numeric (pentru apa A = 1.146, pentru aer A = 40.6).
Calculat prin formulele 4.1 - 4.3 viteze cad cereale forma finală sferică în apă depășește valabil ca toate granule minerale primite la clasificarea hidraulică după măcinare, au o formă diferită - plat, unghiular, alungite, rotunjite, și altele.
O metodă universală pentru determinarea ratei finale de incidență a unei particule sferice într-un mediu lichid conform parametrului Reynolds a fost propusă de PV Lyashchenko. Această metodă
ia în considerare ambele tipuri de rezistență pentru orice mediu lichid.
Numărul Reynolds (Re) este raportul dintre produsul vitezei particulelor și diametrul său și densitatea fluidului până la coeficientul de vâscozitate al fluidului.
unde Re este parametrul Reynolds (fără dimensiuni); u este viteza relativă a corpului, m / s; d este diametrul corpului în mișcare, m; A este densitatea lichidului, kg / m3; m este vâscozitatea absolută a lichidului, H # 903; c / m 2.
La Re> 1000, regimul de mișcare a fluidului este turbulent, cu Re Definiția vitezei finale este aceea că pentru parametrii cunoscuți ai particulei și mediului, parametrul Re 2 y este calculat din formula unde d este diametrul particulelor, m; d este densitatea particulelor, kg / m3; D este densitatea mediului (pentru apă D = 1000 kg / m 3); g - accelerația gravitației (g = 9,81 m / s 2); m este coeficientul de vâscozitate a apei m = 0,001 N · s / m 2). Parametrul Re 2 y. inițial propus de PV Lyashchenko, de asemenea, fără dimensiuni, precum numerele Re și y, și se stabilește o conexiune între ele (vezi diagrama din Figura 4.1).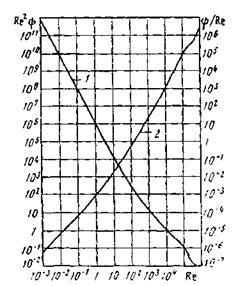
Fig. 4.1. Dependența parametrilor Re 2 y (1) și # 968; / Re (2) de la Re
În diagrama (a se vedea figura 4.1), în funcție de valoarea calculată Re 2 y, se găsește valoarea Re. după care viteza finală este determinată de formula (4.4).
Raportul dintre diametrele particulelor a două minerale diferite care se încadrează la aceeași rată este numit coeficientul de echidistanță.
Coeficientul de echidistanță indică de câte ori particulele minerale ușoare sunt mai mari decât granulele unui mineral greu care are aceeași rată de cădere finală și este determinat pentru particule de orice mărime prin formula:
unde d1 și d2 sunt dimensiunile particulelor egale de minerale ușoare și grele, m; d1 și d2 - densitatea acestor particule, kg / m3; D este densitatea mediei, kg / m3; n = 1 ÷ 3.
În condiții practice de îmbogățire, particulele se mișcă nu în mod liber, ci în spațiu masiv și în spațiu închis, adică în condiții înghesuite.
Viteza incidenței înghețate a particulelor este întotdeauna mai mică decât viteza de cădere liberă și depinde de vâscozitatea mediului, care crește odată cu conținutul de particule solide în acesta.
Aceasta poate fi exprimată prin formula
unde ust este viteza finală a particulelor care se încadrează într-un lichid în condiții strâmte, m / s; u0 este viteza finală de cădere liberă a particulelor, m / s; # 952; - factor de reducere a ratei.
Conform calculelor, # 952; = 0,08 ÷ 0,21.
Legile privind incidența liberă și înghețată a particulelor sunt utilizate în dezvoltarea proceselor de îmbogățire gravitațională, hidroclasificare și clarificare a apelor de șlam.