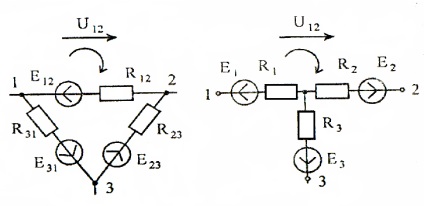
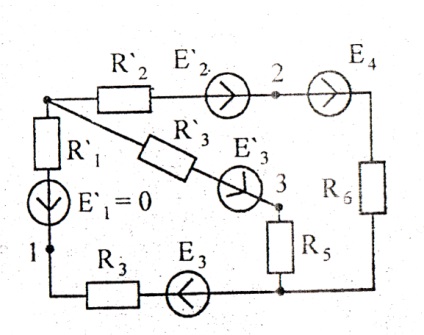
În transformarea unui star triunghi în ramuri ale unei stele echivalente, sunt cuprinse atât elementele pasive (rezistențe), cât și cele active (sursele EMF). Valorile EMF echivalente sunt determinate din condiția ca diferența de potențial să fie egală între nodurile corespunzătoare înainte și după conversie atunci când secțiunea convertită este întreruptă complet de restul circuitului (Figura 15). În acest caz, curentul curge în toate ramurile triunghiului și nu există curenți în ramurile stelei.
Să scriem a doua lege Kirchhoff pentru sucursala R12. E12 triunghi:
Deoarece stresul U12 în ambele scheme trebuie să fie același, obținem
În mod similar și pentru celelalte ramuri pe care le avem
Expresiile (11) - (14) fac posibilă determinarea valorilor EMF echivalente.
Când se schimbă dintr-un triunghi într-o stea echivalentă, pentru a simplifica rezolvarea problemei, magnitudinea emf-ului dintr-o ramură a stelei poate fi aleasă în mod arbitrar. Fie, de exemplu, E3 = 0, atunci din expresiile (13), (14) obținem:
Când trece de la stea la triunghiul echivalent, ca o condiție suplimentară,
Apoi și din expresiile (12) - (14) obținem
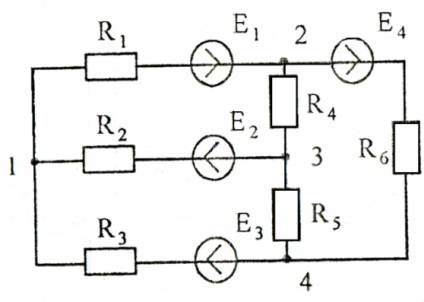
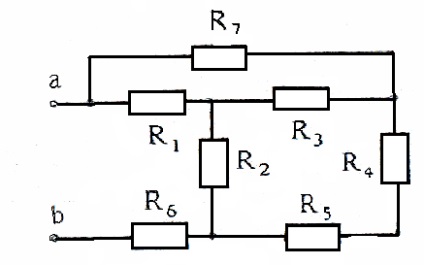
Valorile rezistențelor echivalente ale unei stele și ale unui triunghi sunt determinate de formulele (1) - (6). Luați în considerare, de exemplu, diagrama din Figura 16, care, folosind transformarea unei stele cu ramificații (R1 .E1), (R2 .E2), (R3 .E3) într-un triunghi echivalent, arată ca Figura 17.
Alegem ca o condiție suplimentară
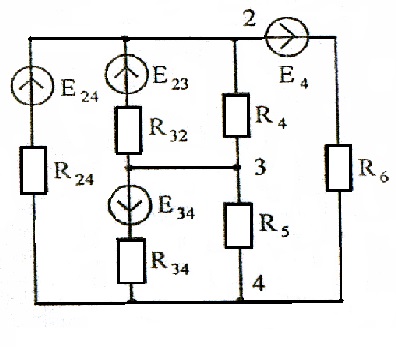
Considerăm transformarea triunghiului 1 2 3 (Figura 16) într-o stea echivalentă, pentru care o selectăm din lanț (Figura 18a).
Subliniază între nodurile unui triunghi și ale unei stele:
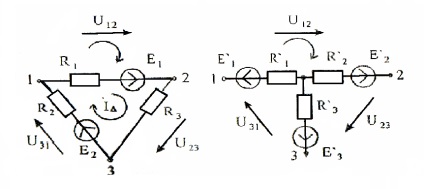
Acceptăm simplificarea. atunci:
Ca rezultat, schema (Figura 16) ia forma prezentata in Figura 19.
Determinați rezistența echivalentă RE (Figura 20, 21, 22) în raport cu bornele indicate, dacă rezistența este de 10 Ohm. Datele care trebuie luate de la fila. 1-3 (numărul variantei corespunde numărului de serie al elevului din jurnal, numărul 11 corespunde unei singure variante).
Numărul sarcinilor 2. Circuite sinusoidale monofazate
Sarcina de a calcula circuitul electric este de a determina curenții din ramificațiile sale, tensiunile pe secțiunile circuitului sau potențialul nodurilor. În acest caz se stabilesc următorii parametri: configurația circuitului, parametrii elementelor sale și EMF, surse. Pentru a calcula curenții în circuitele electrice complexe, se utilizează metodele ecuațiilor Kirchhoff, curenții de contur, potențialele nodale, generatorul echivalent.
Metoda ecuației Kirchhoff
Calculul circuitelor electrice liniare prin metoda legilor lui Kirchhoff reduce la rezolvarea sistemelor de ecuații algebrice în raport cu curenții necunoscuți. Deoarece numărul de curenți necunoscuți într-un circuit dat este egal cu numărul de ramificații n al acestui circuit, sistemul de ecuații algebrice trebuie să aibă o ordine n-a.
Fie k numărul de noduri din circuit. Din principiul continuității curentului că numărul de ecuații liniar independente, care pot fi formate pe prima lege a lui Kirchhoff ecuații .Nedostayuschie al căror număr egal (k-1) [n- (k-1)], sunt preparate prin a doua lege a lui Kirchhoff a circuitelor independente , care nu conține surse curente. Contururile sunt independente dacă fiecare ramură include o ramură care nu aparține tuturor celorlalte.
Luați în considerare, de exemplu, calculul curentului din circuit (Figura 24), care conține 6 ramificații, 4 noduri și 3 circuite independente. Alegem în mod arbitrar direcția curentului în ramuri și direcția de traversare a circuitelor independente. Primele trei ecuații (4 - 1 = 3) vor fi scrise în conformitate cu prima lege a lui Kirchhoff, iar celelalte trei (6 - 3 = 3) - potrivit celei de-a doua lege a lui Kirchhoff:
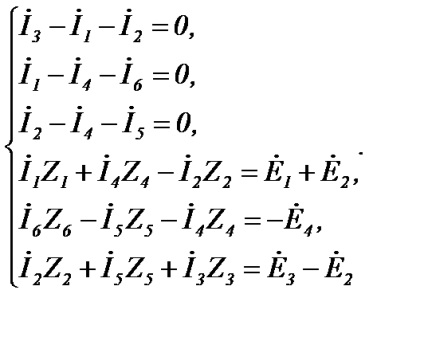
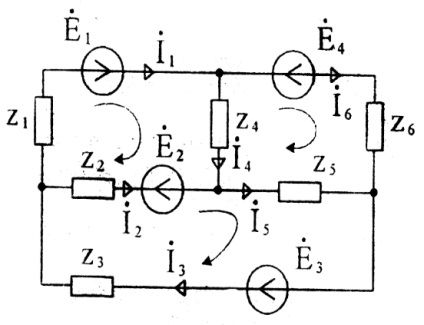
Soluția sistemului de ecuații obținut dă curenții doriți. Dacă lanțul conține ramuri m cu surse curente, atunci numărul de curenți necunoscuți scade la (n-m). Conform primei legi a numărului Kirchhoff de ecuații rămâne neschimbat (k-1), iar a doua lege a lui Kirchhoff scade în consecință numărul de ramuri din sursele de curent [n (k-1) -m].
Astfel, pentru diagrama din figura 25 care conține 6 ramificații și o sursă de curent, este necesar să se compună trei ecuații în conformitate cu prima lege Kirchhoff și două conform celei de-a doua.
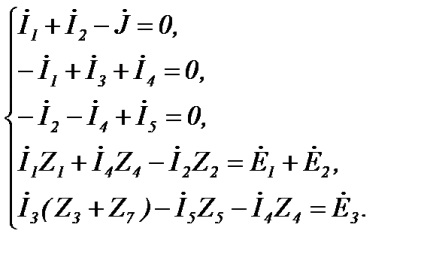
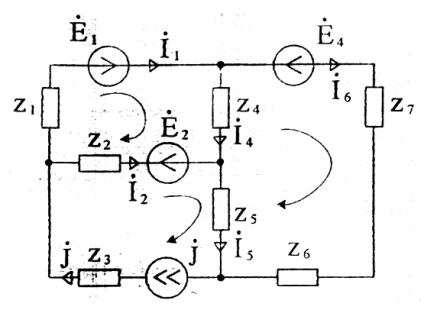
Dacă, ca urmare a calculelor, un anumit curent este negativ, înseamnă că direcția sa efectivă este opusă celei alese.
Dezavantajul acestei metode este ordinea ridicată a sistemului de ecuații pentru calculul circuitelor electrice complexe.
Metoda curenților de contur
Calculul lanțului ramificat poate fi redus la rezolvarea tuturor ecuațiilor [n- (k-1)], compilate conform celei de-a doua lege a lui Kirchhoff. În acest scop, circuitul este considerat ca un set de contururi independente contiguoase și o înlocuire condiționată a curenților necunoscuți în ramuri cu curenți care curg de-a lungul contururilor închise. Ecuațiile compilate în conformitate cu cea de-a doua lege a lui Kirchhoff introduc curenții în circuite independente - curenții de contur.
Curenții reali în ramuri aparținând unui singur contur sunt egali cu curenții de contur corespunzători (dar pot diferi de acestea în direcția). Curenții în comun pentru două sau mai multe ramuri ale contururilor sunt definite ca suma algebrică a curenților de contur corespunzători. Prima lege Kirchhoff va fi executată automat. Direcția curenților de buclă este aleasă arbitrar, iar prin ocolirea contururilor suntem de acord să efectuăm în direcția curenților de buclă.
Pentru un circuit cu surse EMF, sistemul de ecuații compilat pentru bucle independente din legea a doua Kirchhoff conține ecuații de tipul
unde sunt curenți de contur;
- suma rezistențelor ramurilor care formează un contur m independent (rezistența conturului);
- suma EMF a acestui circuit;
Zmq este rezistența ramurii comune pentru m-și conturul q (rezistență de cuplare).
Dacă în ramurile comune (contiguoase) direcțiile curenților de contur coincid, atunci rezistența de cuplare este considerată pozitivă, dacă curenții sunt direcționați opus, atunci rezistența este negativă. Rezistența la contur este întotdeauna acceptată ca pozitivă.
Atunci când scrieți partea dreaptă a ecuațiilor EMF, ale căror direcții coincid cu direcția adoptată a curentului de buclă (bypass), se presupune că este pozitivă și pentru curenții negativi direcționați opus.
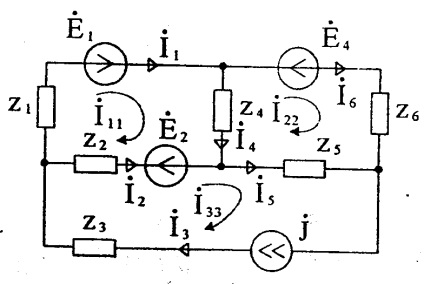
Să scriem sistemul de ecuații prin metoda curenților de buclă pentru circuit Figura 26:
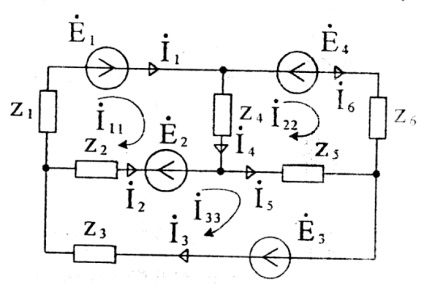
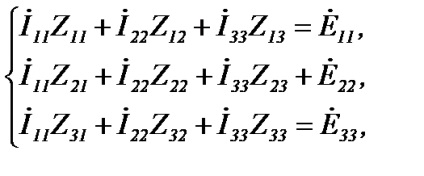
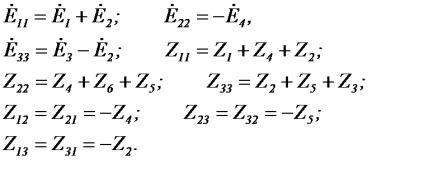
După rezolvarea sistemului de ecuații pentru curenții de contur, descoperim curenții din ramuri:
În prezența unei ramificații cu o sursă de curent, este selectat un circuit suplimentar care include acest circuit. Ecuația pentru conturul suplimentar nu este compilată, deoarece curentul bucla este egal cu curentul sursei. Sunt luate în considerare scăderile de tensiune ale rezistenței de comunicare cu alte surse de curent (curentul de buclă). Astfel, pentru un lanț (Figura 27) sistemul de ecuații are forma
Metoda potențialului nodal
Dacă numărul de noduri dintr-un circuit electric ramificat este mai mic decât unul din numărul de circuite independente (k-1)<[n-(k-1)], удобно воспользоваться методом узловых потенциалов. Он сводится к составлению и решению системы алгебраических уравнений (k-1)-го порядка относительно неизвестных потенциалов (узловых потенциалов). При этом потенциал одного из узлов схемы полагают равным нулю.
Ecuațiile cu potențial nodal rezultă din prima lege a lui Kirchhoff. După ce a descoperit potențiale necunoscute, curenții din ramuri sunt determinați de legea lui Ohm.
Ecuațiile care intră în sistem sunt de același tip și pentru nodul m au următoarea formă:
unde este suma conductivităților tuturor ramurilor convergente la nodul m;
- conductivitatea nodului de conectare ramură m cu nod q. Dacă nu există ramificații între noduri, atunci conductivitatea corespunzătoare este zero;
- Sursele EMF situate în ramificație între nodurile m sau q.
În acest caz, EMF direcționat către nodul m (față de care se compune ecuația) este considerat pozitiv, iar nodurile direcționate din acest nod sunt negative.
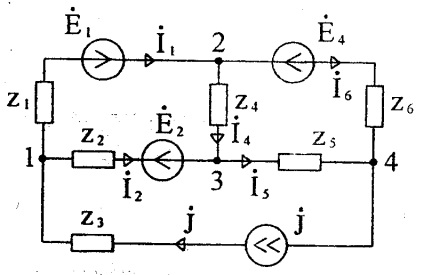
Să compunem sistemul de ecuații pentru circuitul Figura 28, presupunând:
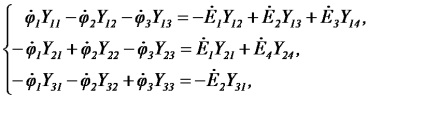
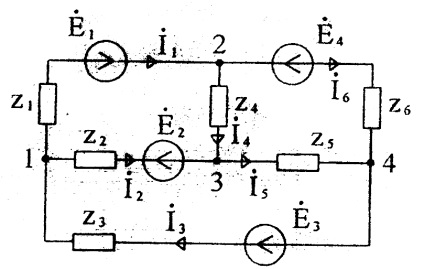
După determinarea potențialelor, găsim curenți conform legii lui Ohm:
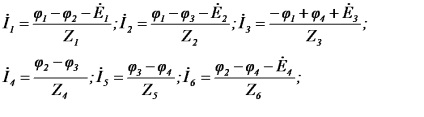
Dacă ramura conține o sursă de curent, atunci conductivitatea acesteia este zero, deoarece rezistența internă a sursei de curent este infinită. Dacă curentul curge de la sursa curentă la cel de-al treilea, trebuie să fie inclus în partea dreaptă a ecuației cu un semn plus, dacă acesta curge, apoi cu un semn minus. Deci, pentru un lanț (Figura 29) sistemul de ecuații arată ca:
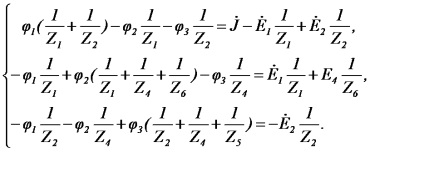
În orice circuit electric, conform legii conservării energiei, cantitatea de energie a surselor produse pe unitate de timp trebuie să fie egală cu puterea consumatorilor:
Orice încălcare a acestor relații indică o inexactitate a calculelor efectuate.
Puterea activă și reactivă a surselor poate fi găsită ca părți reale și imaginare ale puterii complexe totale a surselor:
unde este complexul curent conjugat
Dacă direcția actuală coincide cu direcția sursei EMF, atunci produsul intră în partea stângă a ecuației cu un semn plus, altfel - cu un semn minus.
Dacă circuitul electric conține o sursă de curent j, atunci
unde este tensiunea la bornele sursei de curent.
Puterea activă a consumatorilor:
unde Iq este valoarea efectivă a curentului ramurii qth care conține rezistența activă Rq.
Puterea reactivă a consumatorilor:
Pentru inductanță, produsul I 2 XL este inclus în suma cu semnul plus, pentru capacitatea I 2 Xc - cu semnul minus.